Слайд 2
Логические основы компьютеров
3.1 Логика и компьютер
Слайд 3
Логика, высказывания
Логика (др.греч. λογικος) – это наука о
том, как правильно рассуждать, делать выводы, доказывать утверждения.
Формальная логика
отвлекается от конкретного содержания, изучает только истинность и ложность высказываний.
Логическое высказывание – это повествовательное предложение, относительно которого можно однозначно сказать, истинно оно или ложно.
Слайд 4
Высказывание или нет?
Сейчас идет дождь.
Жирафы летят на север.
История
– интересный предмет.
У квадрата – 10 сторон и все
разные.
Красиво!
В городе N живут 2 миллиона человек.
Который час?
Слайд 5
Логика и компьютер
Двоичное кодирование – все виды информации
кодируются с помощью 0 и 1.
Задача – разработать оптимальные
правила обработки таких данных.
Почему «логика»?
Результат выполнения операции можно представить как истинность (1) или ложность (0) некоторого высказывания.
Джордж Буль разработал основы алгебры,
в которой используются только 0 и 1
(алгебра логики, булева алгебра).
Слайд 6
Логические основы компьютеров
3.2 Логические операции
Слайд 7
Обозначение высказываний
A – Сейчас идет дождь.
B – Форточка
открыта.
простые высказывания (элементарные)
Составные высказывания строятся из простых с помощью
логических связок (операций) «и», «или», «не», «если … то», «тогда и только тогда» и др.
A и B
A или не B
если A, то B
A тогда и только
тогда, когда B
Сейчас идет дождь и открыта форточка.
Сейчас идет дождь или форточка закрыта.
Если сейчас идет дождь, то форточка открыта.
Дождь идет тогда и только тогда, когда открыта форточка.
Слайд 8
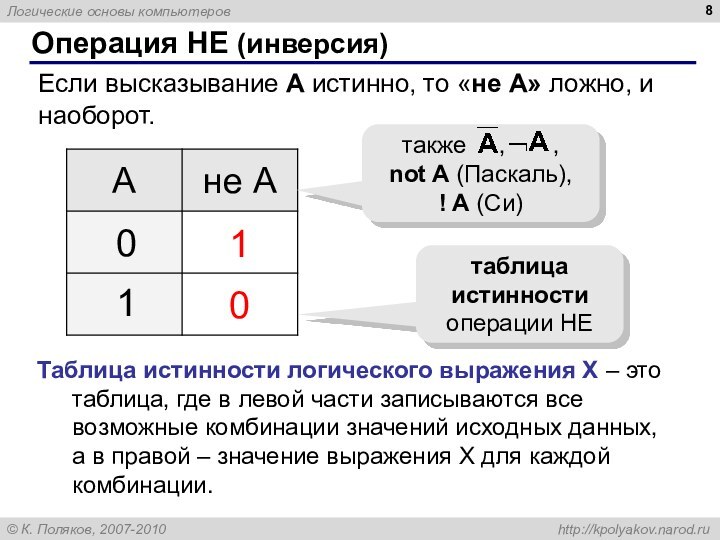
Операция НЕ (инверсия)
Если высказывание A истинно, то «не
А» ложно, и наоборот.
1
0
0
1
таблица истинности операции НЕ
также
, ,
not A (Паскаль),
! A (Си)
Таблица истинности логического выражения Х – это таблица, где в левой части записываются все возможные комбинации значений исходных данных, а в правой – значение выражения Х для каждой комбинации.
Слайд 9
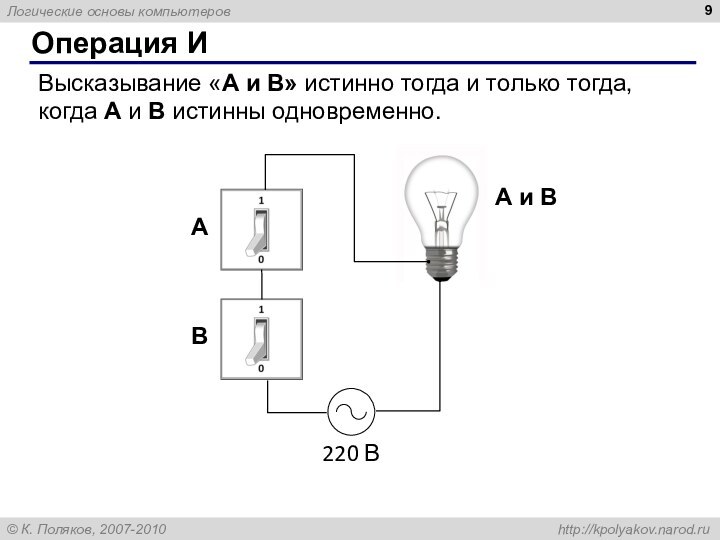
Операция И
Высказывание «A и B» истинно тогда и
только тогда, когда А и B истинны одновременно.
A и
B
A
B
Слайд 10
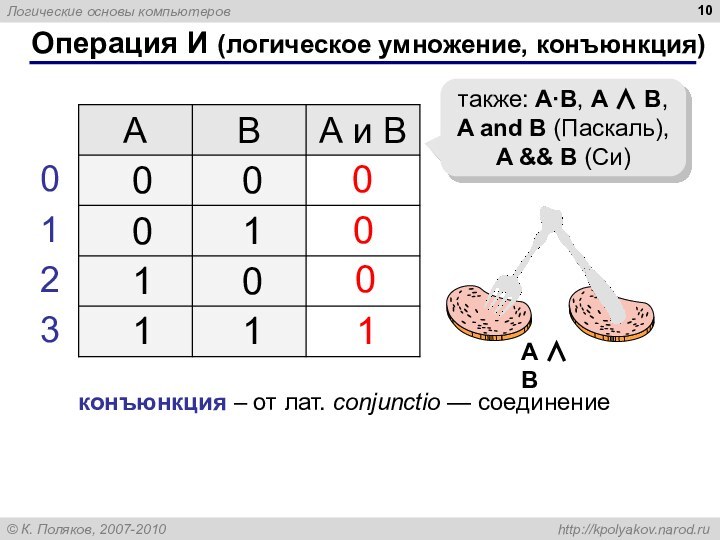
Операция И (логическое умножение, конъюнкция)
1
0
также: A·B, A
B,
A and B (Паскаль),
A && B (Си)
0
0
конъюнкция –
от лат. conjunctio — соединение
A B
Слайд 11
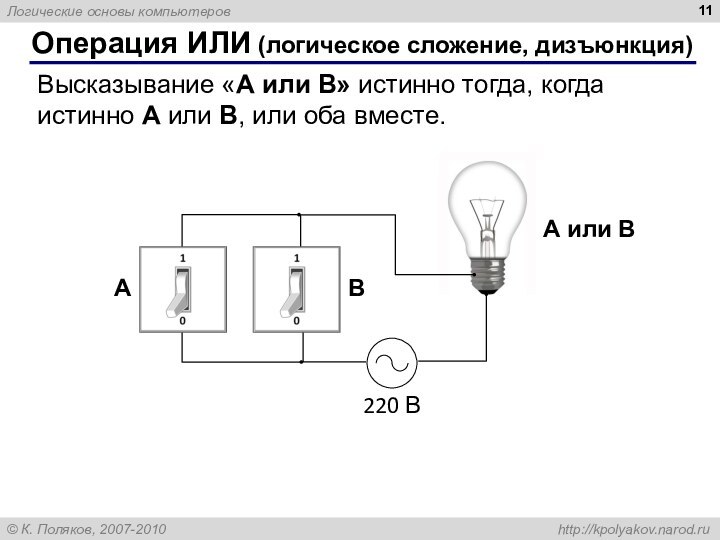
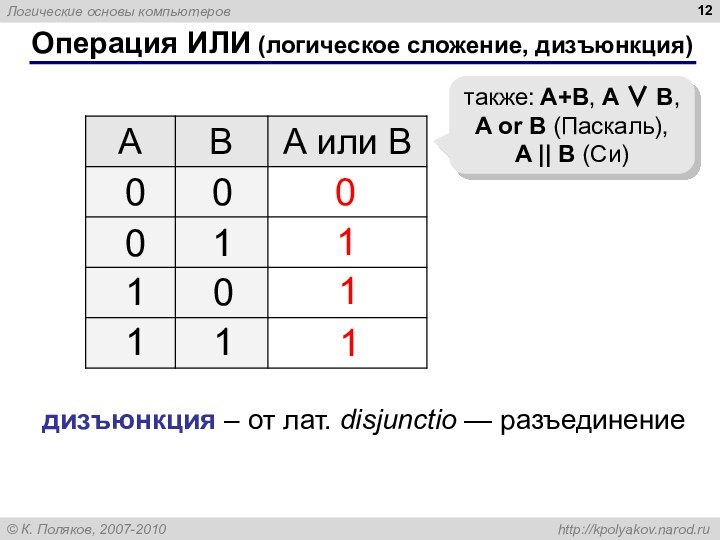
Операция ИЛИ (логическое сложение, дизъюнкция)
Высказывание «A или B»
истинно тогда, когда истинно А или B, или оба
вместе.
A или B
A
B
Слайд 12
Операция ИЛИ (логическое сложение, дизъюнкция)
1
0
также: A+B, A
B,
A or B (Паскаль),
A || B (Си)
1
1
дизъюнкция –
от лат. disjunctio — разъединение
Слайд 13
Задачи
В таблице приведены запросы к поисковому серверу. Расположите
номера запросов в порядке возрастания количества страниц, которые найдет
поисковый сервер по каждому запросу. Для обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» – &.
1) принтеры & сканеры & продажа
2) принтеры & продажа
3) принтеры | продажа
4) принтеры | сканеры | продажа
1 2 3 4
Слайд 14
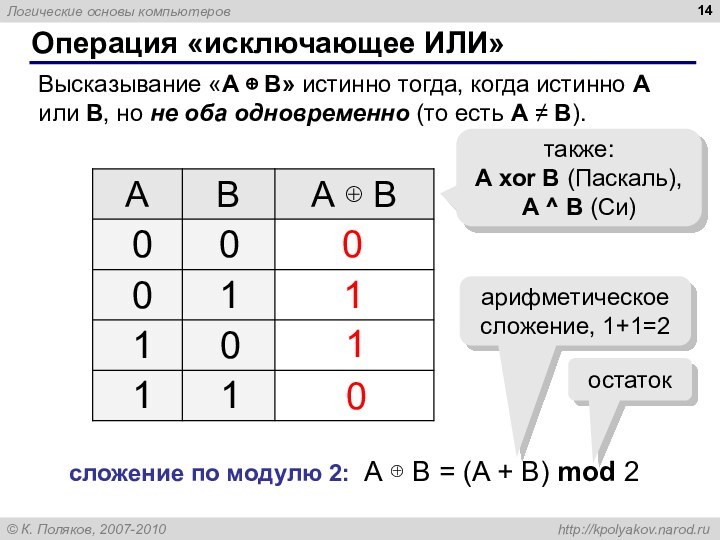
Операция «исключающее ИЛИ»
Высказывание «A B» истинно тогда,
когда истинно А или B, но не оба одновременно
(то есть A B).
0
0
также:
A xor B (Паскаль),
A ^ B (Си)
1
1
сложение по модулю 2: А B = (A + B) mod 2
арифметическое сложение, 1+1=2
остаток
Слайд 15
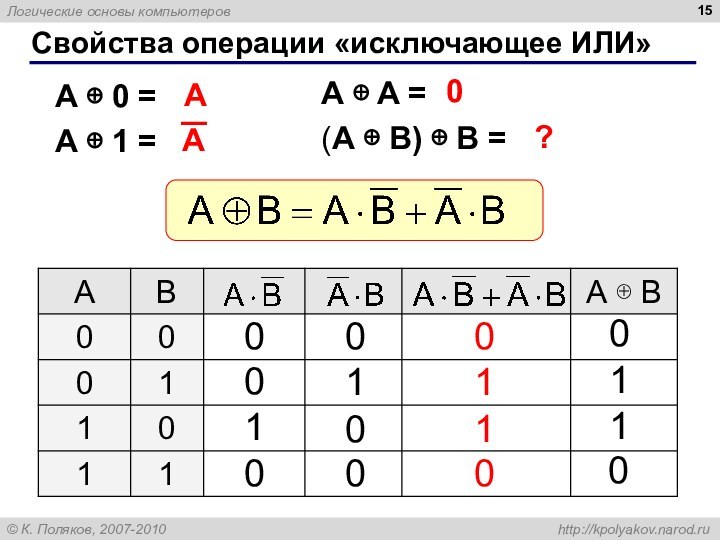
Свойства операции «исключающее ИЛИ»
A A =
(A
B) B =
A 0 =
A
1 =
A
0
?
Слайд 16
Импликация («если …, то …»)
Высказывание «A B»
истинно, если не исключено, что из А следует B.
A – «Работник хорошо работает».
B – «У работника хорошая зарплата».
1
1
1
0
Слайд 17
Импликация («если …, то …»)
«Если Вася идет гулять,
то Маша сидит дома».
A – «Вася идет гулять».
B – «Маша сидит дома».
Маша может пойти гулять
(B=0), а может и не пойти (B=1)!
Слайд 18
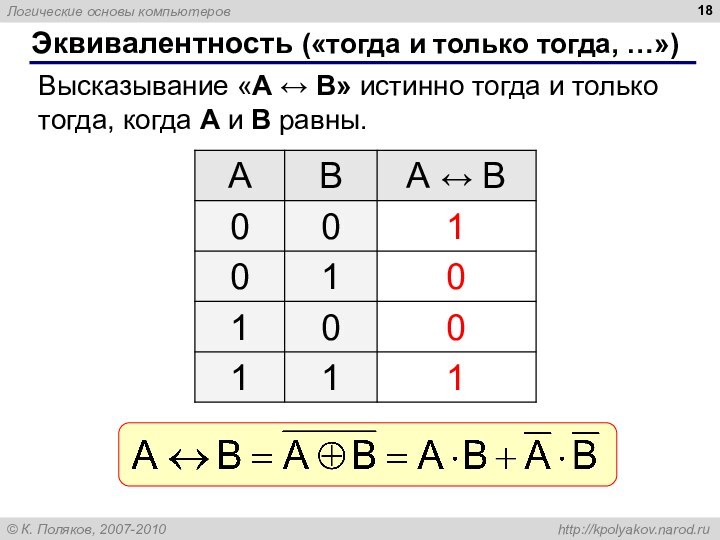
Эквивалентность («тогда и только тогда, …»)
Высказывание «A
B» истинно тогда и только тогда, когда А и
B равны.
Слайд 19
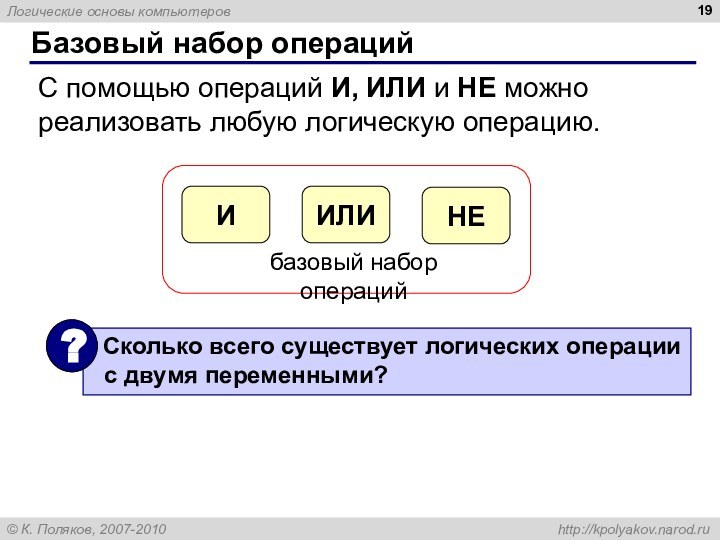
Базовый набор операций
С помощью операций И, ИЛИ и
НЕ можно реализовать любую логическую операцию.
Слайд 20
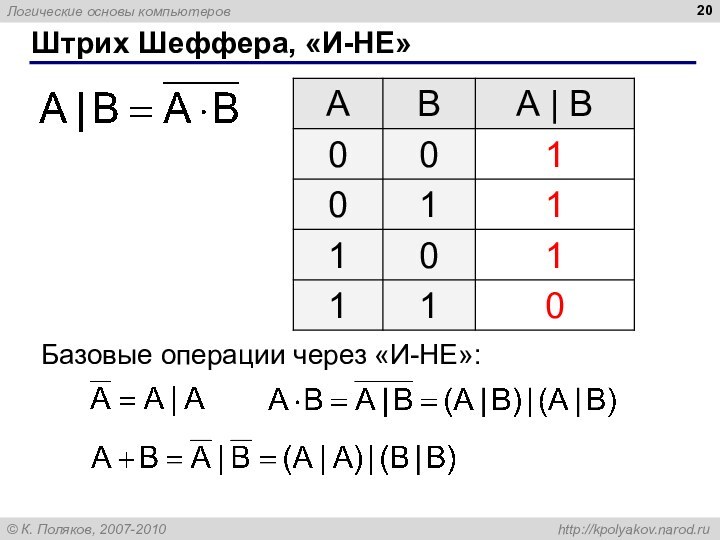
Штрих Шеффера, «И-НЕ»
Базовые операции через «И-НЕ»:
Слайд 21
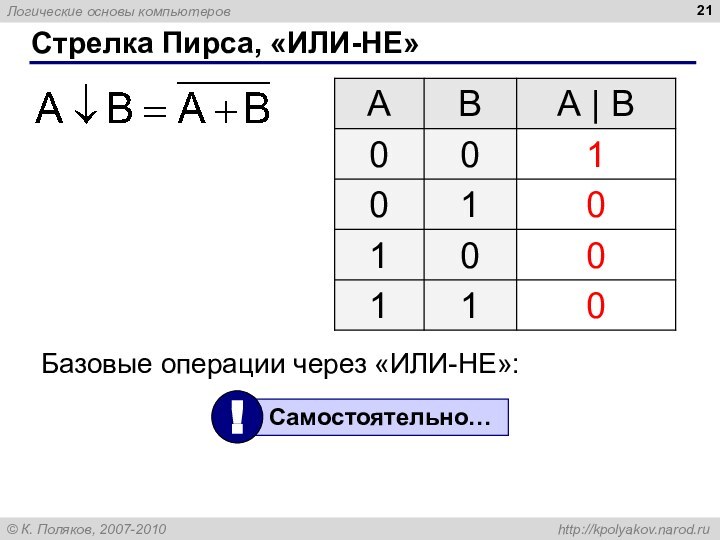
Стрелка Пирса, «ИЛИ-НЕ»
Базовые операции через «ИЛИ-НЕ»:
Слайд 22
Формализация
Прибор имеет три датчика и может работать, если
два из них исправны. Записать в виде формулы ситуацию
«авария».
A – «Датчик № 1 неисправен».
B – «Датчик № 2 неисправен».
C – «Датчик № 3 неисправен».
Аварийный сигнал:
X – «Неисправны два датчика».
X – «Неисправны датчики № 1 и № 2» или
«Неисправны датчики № 1 и № 3» или
«Неисправны датчики № 2 и № 3».
логическая формула
Слайд 23
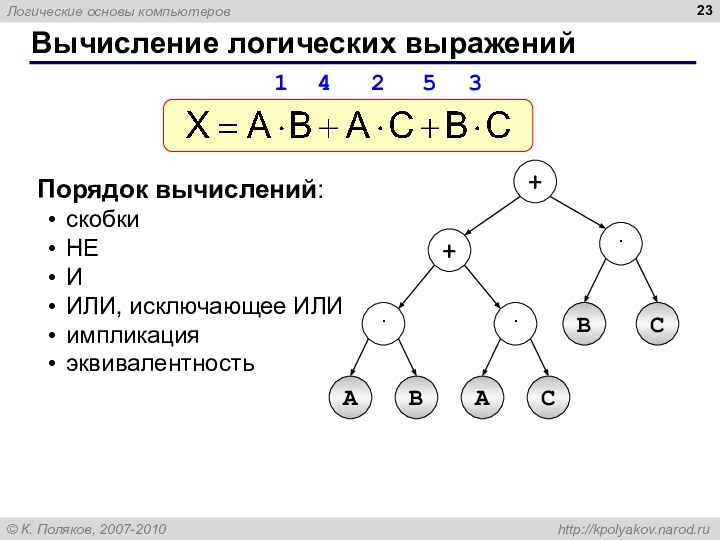
Вычисление логических выражений
Порядок вычислений:
скобки
НЕ
И
ИЛИ, исключающее ИЛИ
импликация
эквивалентность
A
B
+
+
B
C
A
С
1 4
2 5 3
Слайд 24
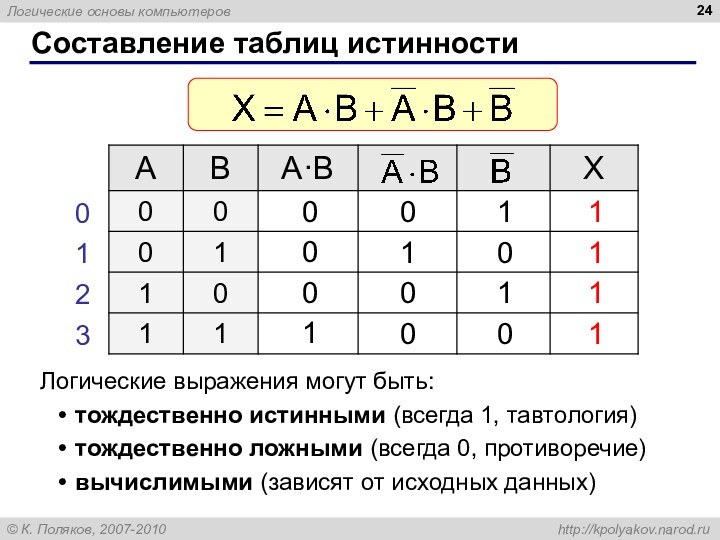
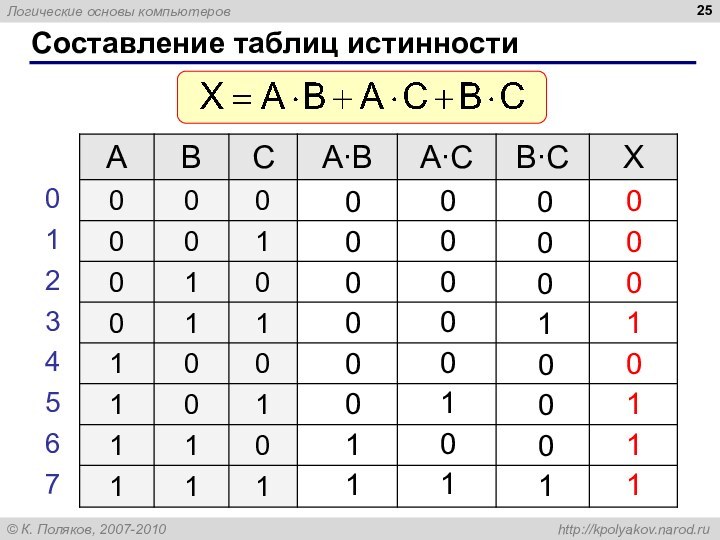
Составление таблиц истинности
Логические выражения могут быть:
тождественно истинными (всегда
1, тавтология)
тождественно ложными (всегда 0, противоречие)
вычислимыми (зависят от исходных
данных)
Слайд 26
Задачи (таблица истинности)
Символом F обозначено одно из указанных
ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F. Какое выражение соответствует F?
¬X ¬Y ¬Z
X Y Z
X Y Z
¬X ¬Y ¬Z
Слайд 27
Логические основы компьютеров
3.3 Диаграммы
Слайд 28
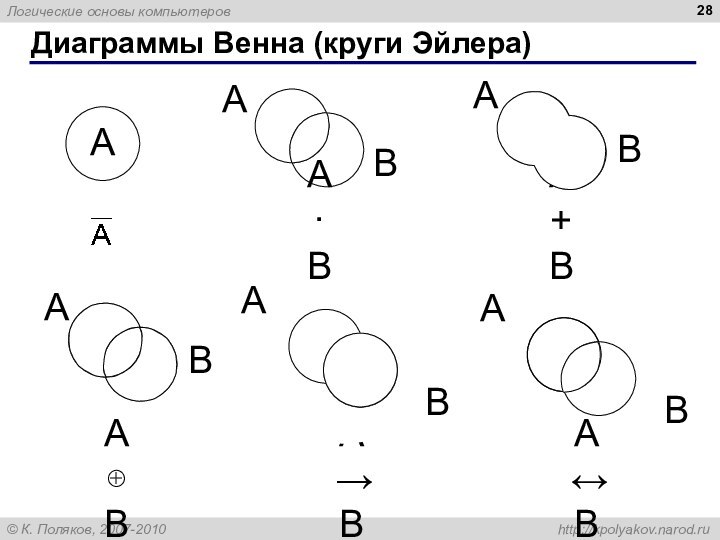
Диаграммы Венна (круги Эйлера)
A·B
A+B
AB
AB
AB
Слайд 29
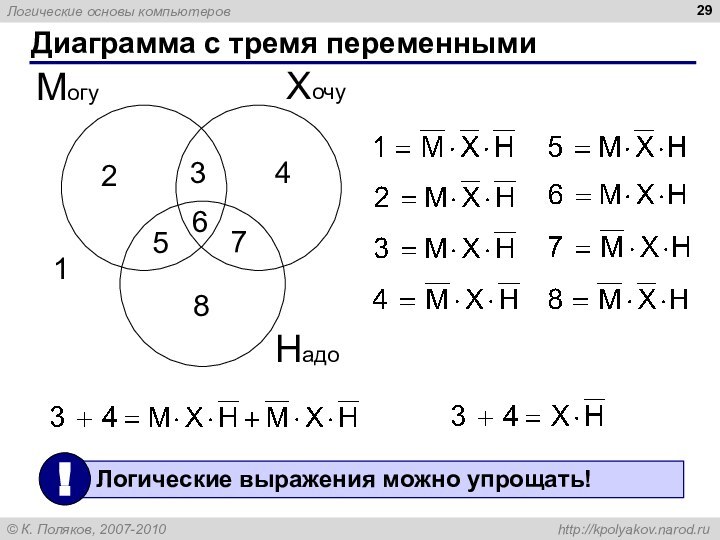
Диаграмма с тремя переменными
Хочу
Могу
Надо
1
2
3
4
5
6
7
8
Слайд 30
Известно количество сайтов, которых находит поисковый сервер по
следующим запросам :
Сколько сайтов будет найдено по запросу
огурцы | помидоры
Задачи
Слайд 31
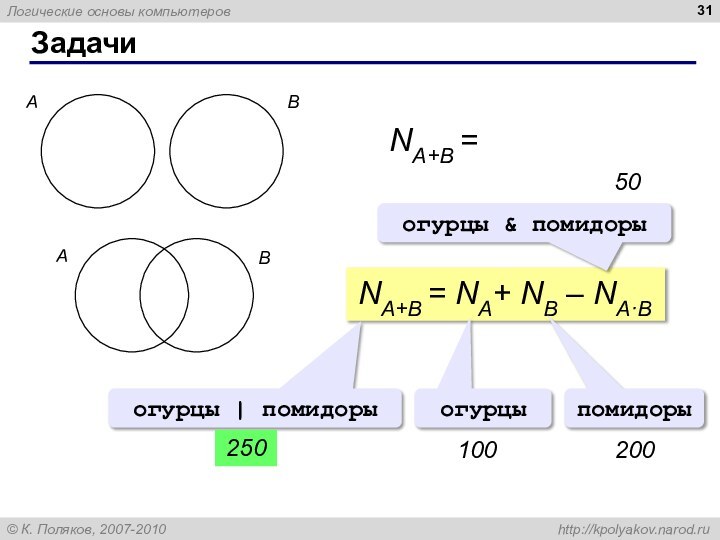
Задачи
NA+B = NA+ NB
A
B
A
B
NA+B = NA+ NB –
NA·B
огурцы | помидоры
50
огурцы
помидоры
100
200
огурцы & помидоры
250
Слайд 32
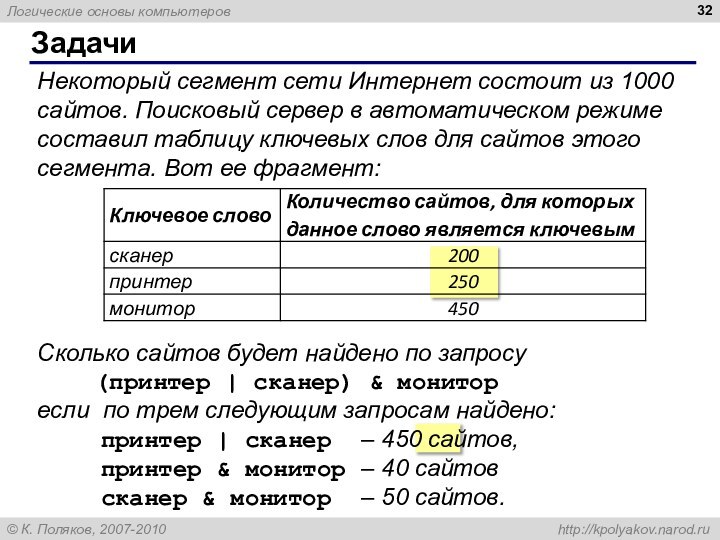
Некоторый сегмент сети Интернет состоит из 1000 сайтов.
Поисковый сервер в автоматическом режиме составил таблицу ключевых слов
для сайтов этого сегмента. Вот ее фрагмент:
Сколько сайтов будет найдено по запросу
(принтер | сканер) & монитор
если по трем следующим запросам найдено:
принтер | сканер – 450 сайтов,
принтер & монитор – 40 сайтов
сканер & монитор – 50 сайтов.
Задачи
Слайд 33
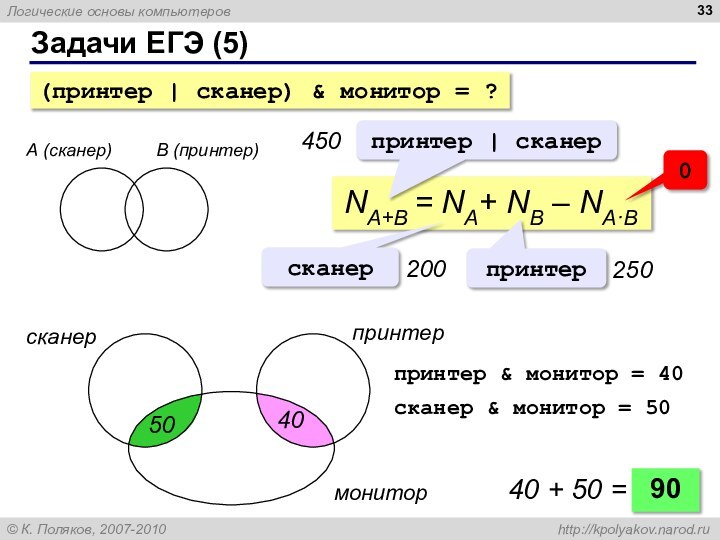
Задачи ЕГЭ (5)
А (сканер)
B (принтер)
NA+B = NA+ NB
– NA·B
принтер | сканер
450
сканер
принтер
200
250
0
сканер
принтер
монитор
90
40 + 50 =
принтер &
монитор = 40
сканер & монитор = 50
50
40
(принтер | сканер) & монитор = ?
Слайд 34
Логические основы компьютеров
3.4 Упрощение логических выражений
Слайд 36
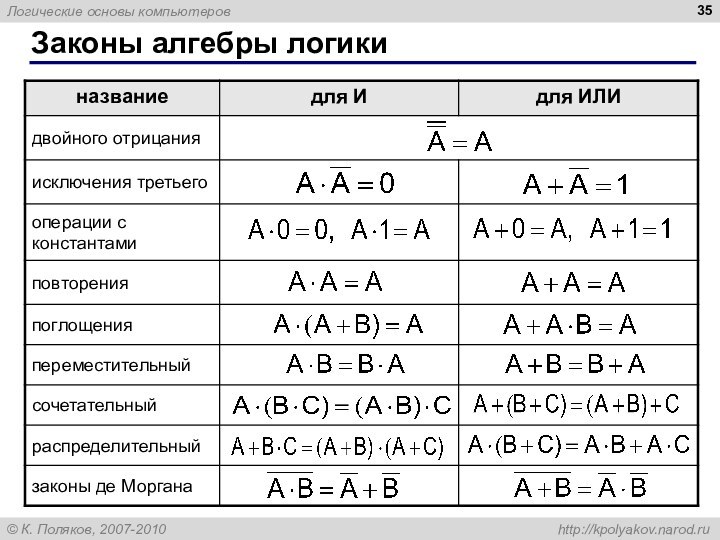
Упрощение логических выражений
Шаг 1. Заменить операции на
их выражения через И, ИЛИ и НЕ:
Шаг 2. Раскрыть
инверсию сложных выражений по формулам де Моргана:
Шаг 3. Используя законы логики, упрощать выражение, стараясь применять закон исключения третьего.
Слайд 37
Упрощение логических выражений
раскрыли
формула де Моргана
распределительный
исключения третьего
повторения
поглощения
Слайд 38
Задачи (упрощение)
Какое логическое выражение равносильно выражению
A
¬(¬B C)?
¬A ¬B ¬C
A ¬B ¬C
A B ¬C
A ¬B C
Слайд 39
Логические уравнения
A=0, B=1, C – любое
2 решения: (0,
1, 0), (0, 1, 1)
или
A=1, B=0, C=1
K=1, L=1,
M
и N – любые
4 решения
M=1, L=1, N=1,
K – любое
2 решения
K=1, L=1, M=0,
N – любое
2 решения
Слайд 40
Логические основы компьютеров
3.5 Синтез логических выражений
Слайд 41
Синтез логических выражений
Шаг 1. Отметить строки в таблице,
где X = 1.
Шаг 2. Для каждой из них
записать логическое выражение, которое истинно только для этой строки.
Шаг 3. Сложить эти выражения и упростить результат.
распределительный
исключения третьего
исключения третьего
распределительный
Слайд 42
Синтез логических выражений (2 способ)
Шаг 1. Отметить строки
в таблице, где X = 0.
Шаг 2. Для каждой
из них записать логическое выражение, которое истинно только для этой строки.
Шаг 3. Сложить эти выражения и упростить результат, который равен .
Шаг 4. Сделать инверсию.
Слайд 43
Синтез логических выражений (3 способ)
Шаг 1. Отметить строки
в таблице, где X = 0.
Шаг 2. Для каждой
из них записать логическое выражение, которое ложно только для этой строки.
Шаг 3. Перемножить эти выражения и упростить результат.
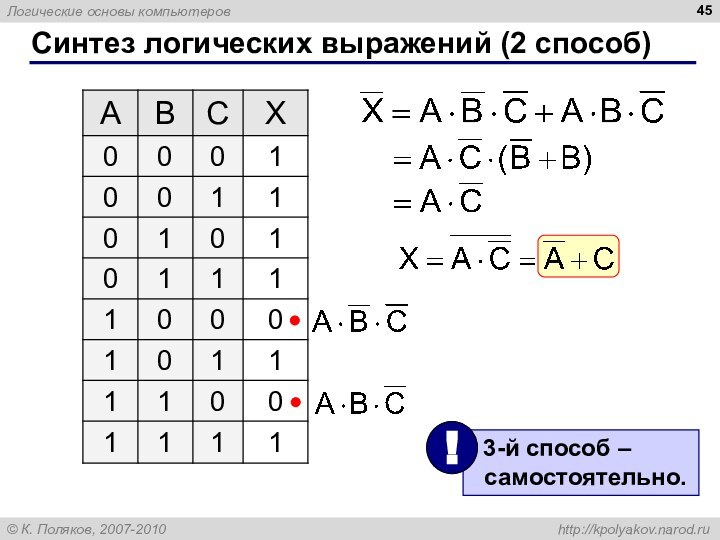
Слайд 45
Синтез логических выражений (2 способ)
Слайд 46
Логические основы компьютеров
3.6 Предикаты и кванторы
Слайд 47
Предикаты
Предикат (логическая функция) – это утверждение, содержащее переменные.
Предикат-свойство
– от одной переменной:
P(N) = «В городе N живут
более 2 млн человек»
P(Москва) = 1
P(Якутск) = 0
Простое(x) = «x – простое число»
Спит(x) = «x всегда спит на уроке»
Предикат-отношение – от нескольких переменных:
Больше(x, y) = «x > y»
Живет(x, y) = «x живет в городе y»
Любит(x, y) = «x любит y»
Слайд 48
Предикаты и кванторы
Предикаты задают множества:
Предикаты, которые всегда истинны:
для
всех вещественных чисел
«Для любого допустимого x утверждение P(x) истинно»:
высказывание
квантор
Квантор
– знак, обозначающий количество.
А
(all – все)
E
(exists – существует)
Слайд 49
Кванторы
Какой квантор использовать?
« … моря соленые».
« …
кошки серые».
« … числа чётные».
« …
окуни – рыбы».
« … прямоугольники – квадраты».
« … квадраты – прямоугольники».
Истинно ли высказывание?
при
при
при
при
Слайд 50
Кванторы
Дано:
A = «Все люди смертны» = 1.
B =
«Сократ – человек» = 1.
Доказать:
C = «Сократ смертен» =
1.
Доказательство:
P(x) = «x – человек» Q(x) = «x – смертен»
A = 1:
при «x =Сократ»
B = 1:
по свойствам импликации
Слайд 51
Несколько кванторов
– предикат от переменной y
Квантор связывает
одну переменную:
– предикат от переменной x
Два квантора связывают
две переменных:
– высказывание «для любого x существует y, при котором P(x,y)=1»
– высказывание «существует x, такой что при любом y верно P(x,y)=1»
Сравните два последних высказывания при:
Слайд 52
Отрицание
НЕ «для любого x выполняется P(x)»
«существует x, при котором не выполняется P(x)»
НЕ «существует
x, при котором выполняется P(x)»
«для любого x не выполняется P(x)»
Слайд 53
Логические основы компьютеров
3.7 Логические элементы компьютера
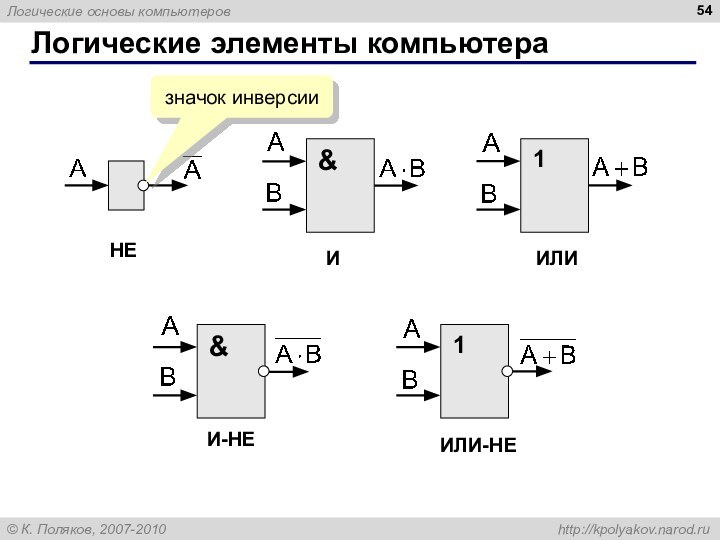
Слайд 54
Логические элементы компьютера
НЕ
И
ИЛИ
ИЛИ-НЕ
И-НЕ
значок инверсии
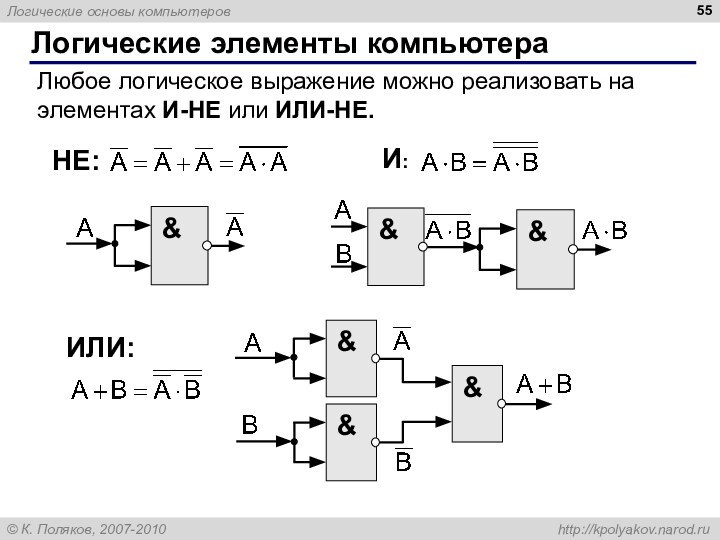
Слайд 55
Логические элементы компьютера
Любое логическое выражение можно реализовать на
элементах И-НЕ или ИЛИ-НЕ.
И:
НЕ:
ИЛИ:
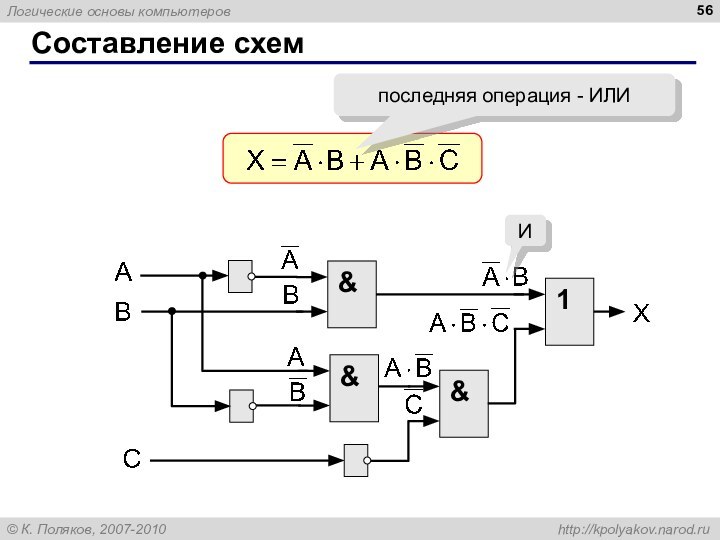
Слайд 56
Составление схем
последняя операция - ИЛИ
&
И
Слайд 57
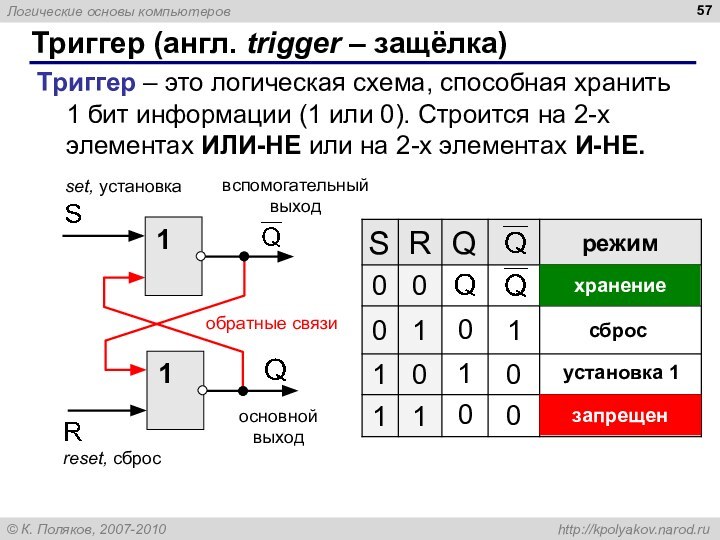
Триггер (англ. trigger – защёлка)
Триггер – это логическая
схема, способная хранить 1 бит информации (1 или 0).
Строится на 2-х элементах ИЛИ-НЕ или на 2-х элементах И-НЕ.
основной
выход
вспомогательный
выход
reset, сброс
set, установка
обратные связи
1
1
0
0
0
0
Слайд 58
Полусумматор
Полусумматор – это логическая схема, способная складывать два
одноразрядных двоичных числа.
0 0
0
1
0 1
1 0
Слайд 59
Сумматор
Сумматор – это логическая схема, способная складывать два
одноразрядных двоичных числа с переносом из предыдущего разряда.
Σ
сумма
перенос
перенос
Слайд 60
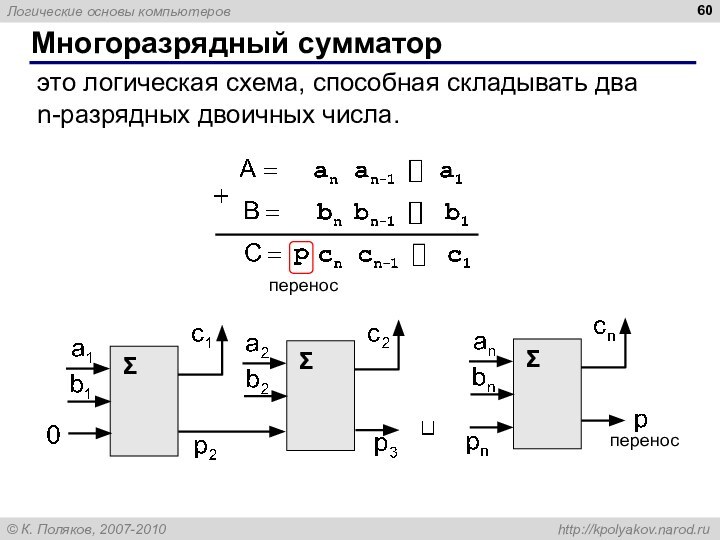
Многоразрядный сумматор
это логическая схема, способная складывать два
n-разрядных
двоичных числа.
перенос
перенос
Слайд 61
Логические основы компьютеров
3.8 Логические задачи
Слайд 62
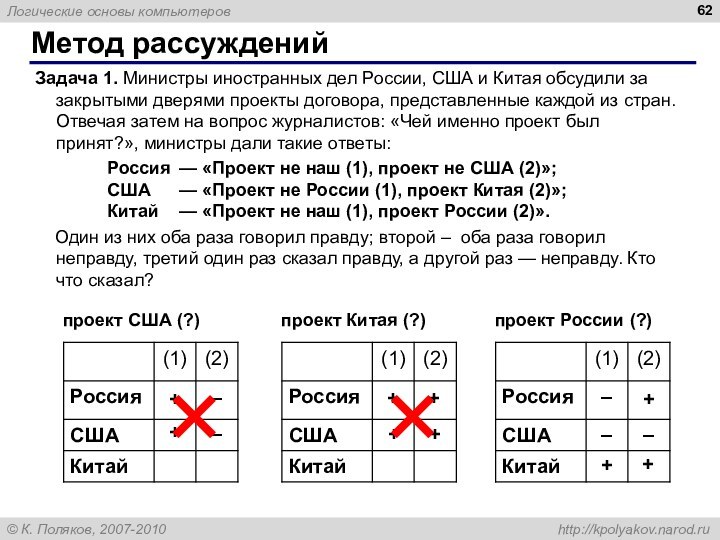
Метод рассуждений
Задача 1. Министры иностранных дел России, США
и Китая обсудили за закрытыми дверями проекты договора, представленные
каждой из стран. Отвечая затем на вопрос журналистов: «Чей именно проект был принят?», министры дали такие ответы:
Россия — «Проект не наш (1), проект не США (2)»;
США — «Проект не России (1), проект Китая (2)»;
Китай — «Проект не наш (1), проект России (2)».
Один из них оба раза говорил правду; второй – оба раза говорил неправду, третий один раз сказал правду, а другой раз — неправду. Кто что сказал?
проект России (?)
–
+
–
–
+
+
проект США (?)
+
–
проект Китая (?)
+
–
+
+
+
+
Слайд 63
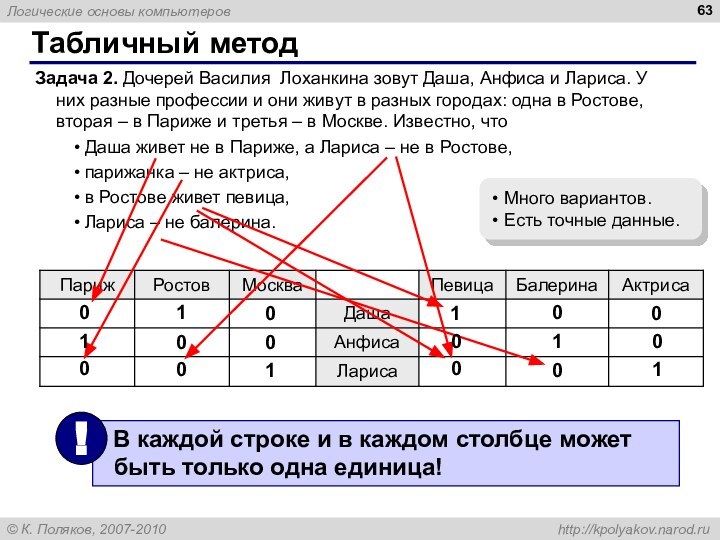
Табличный метод
Задача 2. Дочерей Василия Лоханкина зовут Даша,
Анфиса и Лариса. У них разные профессии и они
живут в разных городах: одна в Ростове, вторая – в Париже и третья – в Москве. Известно, что
Даша живет не в Париже, а Лариса – не в Ростове,
парижанка – не актриса,
в Ростове живет певица,
Лариса – не балерина.
0
0
0
0
1
0
0
0
1
0
0
1
1
0
1
0
0
1
Много вариантов.
Есть точные данные.
Слайд 64
Использование алгебры логики
Задача 3. Следующие два высказывания истинны:
1.
Неверно, что если корабль A вышел в море, то
корабль C – нет.
2. В море вышел корабль B или корабль C, но не оба вместе.
Определить, какие корабли вышли в море.
… если корабль A вышел в море, то корабль C – нет.
1. Неверно, что если корабль A вышел в море, то корабль C – нет.
2. В море вышел корабль B или корабль C, но не оба вместе.
Решение:
Слайд 65
Использование алгебры логики
Задача 4. Когда сломался компьютер, его
хозяин сказал «Память не могла выйти из строя». Его
сын предположил, что сгорел процессор, а винчестер исправен. Мастер по ремонту сказал, что с процессором все в порядке, а память неисправна. В результате оказалось, что двое из них сказали все верно, а третий – все неверно. Что же сломалось?
Решение:
A – неисправен процессор, B – память, C – винчестер
хозяин:
сын:
мастер:
Если ошибся хозяин:
Если ошибся сын:
Если ошибся мастер:
Слайд 66
Использование алгебры логики
Задача 5. На вопрос «Кто из
твоих учеников изучал логику?» учитель ответил: «Если логику изучал
Андрей, то изучал и Борис. Однако неверно, что если изучал Семен, то изучал и Борис». Кто же изучал логику?
Решение:
A – логику изучал Андрей, B – Борис, C – Семен
«Если логику изучал Андрей,
то изучал и Борис».
1 способ:
«Неверно, что если изучал
Семен, то изучал и Борис».
Слайд 67
Использование алгебры логики
Задача 5. На вопрос «Кто из
твоих учеников изучал логику?» учитель ответил: «Если логику изучал
Андрей, то изучал и Борис. Однако неверно, что если изучал Семен, то изучал и Борис». Кто же изучал логику?
Решение:
A – логику изучал Андрей, B – Борис, C – Семен
«Если логику изучал Андрей,
то изучал и Борис».
2 способ:
«Неверно, что если изучал
Семен, то изучал и Борис».
Слайд 68
Использование алгебры логики
Задача 6. Суд присяжных пришел к
таким выводам:
если Аськин не виновен или Баськин виновен, то
виновен Сенькин
если Аськин не виновен, то Сенькин не виновен
Виновен ли Аськин?
Решение:
A – виновен Аськин, B – Баськин, C – Сенькин
«Если Аськин не виновен или Баськин
виновен, то виновен Сенькин».
«Если Аськин не виновен, то
Сенькин не виновен».
Аськин виновен
Слайд 69
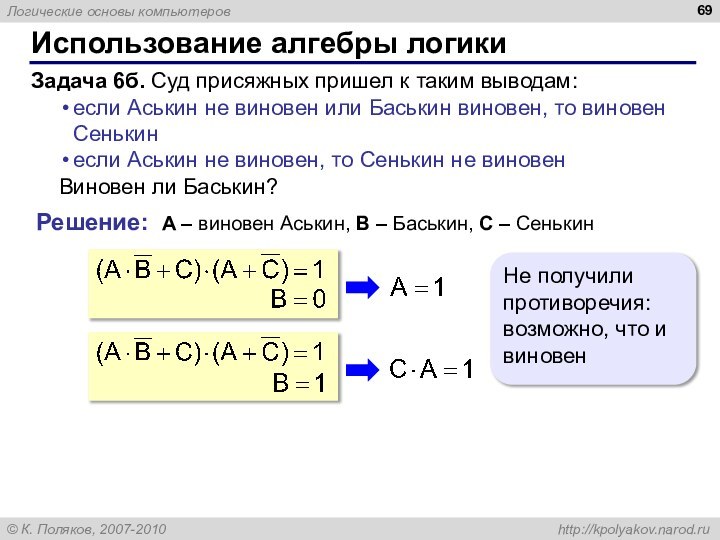
Использование алгебры логики
Задача 6б. Суд присяжных пришел к
таким выводам:
если Аськин не виновен или Баськин виновен, то
виновен Сенькин
если Аськин не виновен, то Сенькин не виновен
Виновен ли Баськин?
Решение:
A – виновен Аськин, B – Баськин, C – Сенькин
Не получили противоречия: возможно, что и виновен
Слайд 70
Использование алгебры логики
Задача 6в. Суд присяжных пришел к
таким выводам:
если Аськин не виновен или Баськин виновен, то
виновен Сенькин
если Аськин не виновен, то Сенькин не виновен
Виновен ли Сенькин?
Решение:
A – виновен Аськин, B – Баськин, C – Сенькин
Не получили противоречия: возможно, что и виновен
Слайд 71
Логические основы компьютеров
Задачи ЕГЭ
Слайд 72
Задачи ЕГЭ
Для какого из указанных значений X истинно
высказывание ¬((X > 2)→(X > 3))?
1) 1 2) 2 3) 3 4) 4
Укажите, какое логическое выражение равносильно выражению A ¬(¬B C).
1) ¬A ¬B ¬C
2) A ¬B ¬C
3) A B ¬C
4) A ¬B C
Слайд 73
Задачи ЕГЭ (2)
Каково наибольшее целое число X, при
котором истинно высказывание
(50 < X·X) → (50 > (X+1)·(X+1))
В
целых числах:
A
B
Слайд 74
Задачи ЕГЭ (6)
Перед началом Турнира Четырех болельщики высказали
следующие предположения по поводу своих кумиров:
А) Макс победит,
Билл – второй;
В) Билл – третий, Ник – первый;
С) Макс – последний, а первый – Джон.
Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов. Какое место на турнире заняли Джон, Ник, Билл, Макс? (В ответе перечислите подряд без пробелов места участников в указанном порядке имен.)
2
3124
1
4
Ответ:
Слайд 75
Задачи ЕГЭ (7)
На одной улице стоят в ряд
4 дома, в каждом из них живет по одному
человеку. Их зовут Василий, Семен, Геннадий и Иван. Известно, что все они имеют разные профессии: скрипач, столяр, охотник и врач. Известно, что
(1) Столяр живет правее охотника.
(2) Врач живет левее охотника.
(3) Скрипач живет с краю.
(4) Скрипач живет рядом с врачом.
(5) Семен не скрипач и не живет рядом со скрипачом.
(6) Иван живет рядом с охотником.
(7) Василий живет правее врача.
(8) Василий живет через дом от Ивана.
Определите, кто где живет, и запишите начальные буквы имен жильцов всех домов слева направо. Например, если бы в домах жили (слева направо) Кирилл, Олег, Мефодий и Пафнутий, ответ был бы КОМП.
Слайд 76
Задача Эйнштейна
Условие: Есть 5 домов разного цвета, стоящие
в ряд. В каждом доме живет по одному человеку
отличной от другого национальности. Каждый жилец пьет только один определенный напиток, курит определенную марку сигарет и держит животное. Никто из пяти человек не пьет одинаковые напитки, не курит одинаковые сигареты и не держит одинаковых животных.
Известно, что:
Англичанин живет в красном доме.
Швед держит собаку.
Датчанин пьет чай.
Зеленой дом стоит слева от белого.
Жилец зеленого дома пьет кофе.
Человек, который курит Pallmall, держит птицу.
Жилец среднего дома пьет молоко.
Жилец из желтого дома курит Dunhill.
Норвежец живет в первом доме.
Курильщик Marlboro живет около того, кто держит кошку.
Человек, который содержит лошадь, живет около того, кто курит Dunhill.
Курильщик Winfield пьет пиво.
Норвежец живет около голубого дома.
Немец курит Rothmans.
Курильщик Marlboro живет по соседству с человеком, который пьет воду.
Вопрос: У кого живет рыба?