Слайд 2
Содержание темы
Понятие вектора. Равенство векторов
Сложение и вычитание векторов.
Сложение
нескольких векторов
Умножение вектора на число
Компланарные вектора. Правило параллелепипеда
Разложение вектора
по трём некомпланарным векторам
Решение задач
Слайд 3
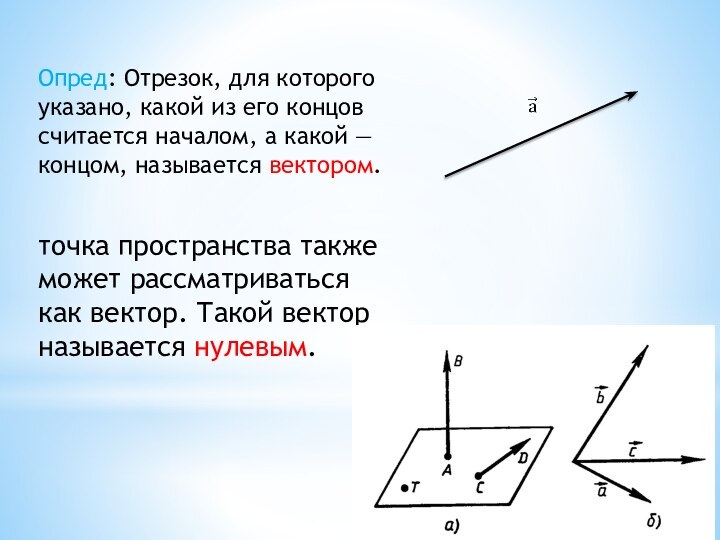
Опред: Отрезок, для которого указано, какой из его
концов считается началом, а какой — концом, называется вектором.
точка пространства также может рассматриваться
как вектор. Такой вектор называется нулевым.
Слайд 5
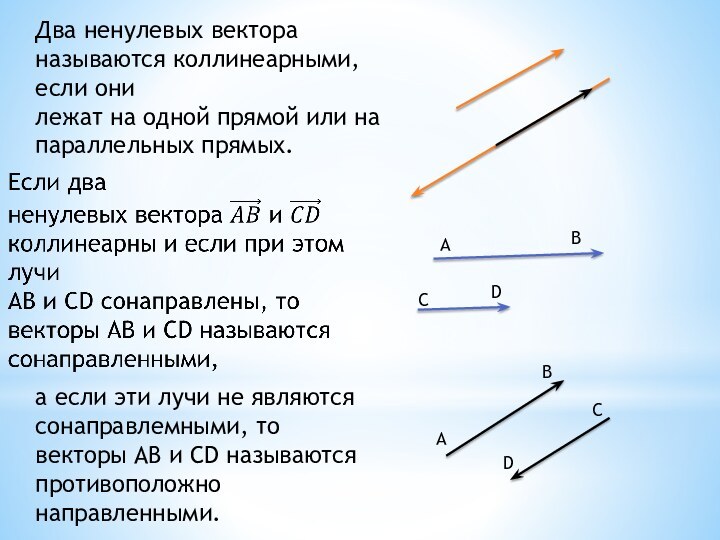
Два ненулевых вектора называются коллинеарными, если они
лежат
на одной прямой или на параллельных прямых.
A
B
C
D
а если
эти лучи не являются сонаправлемными, то
векторы АВ и CD называются противоположно направленными.
A
D
B
C
Слайд 6
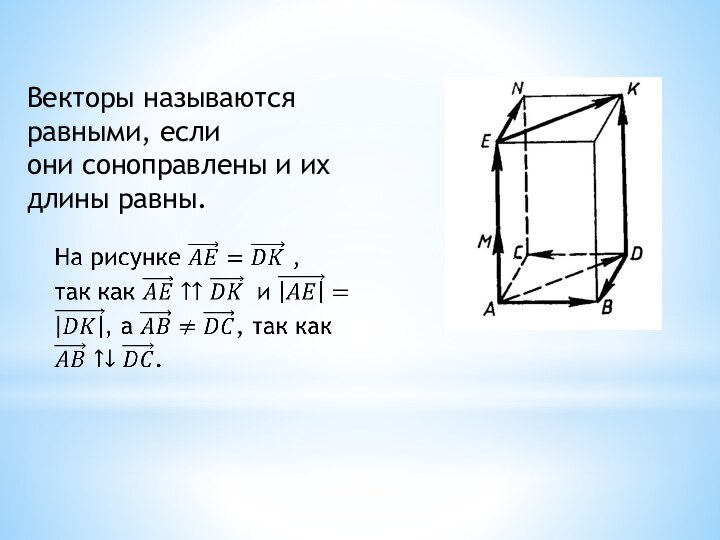
Векторы называются равными, если
они соноправлены и их
длины равны.
Слайд 7
Решение задач
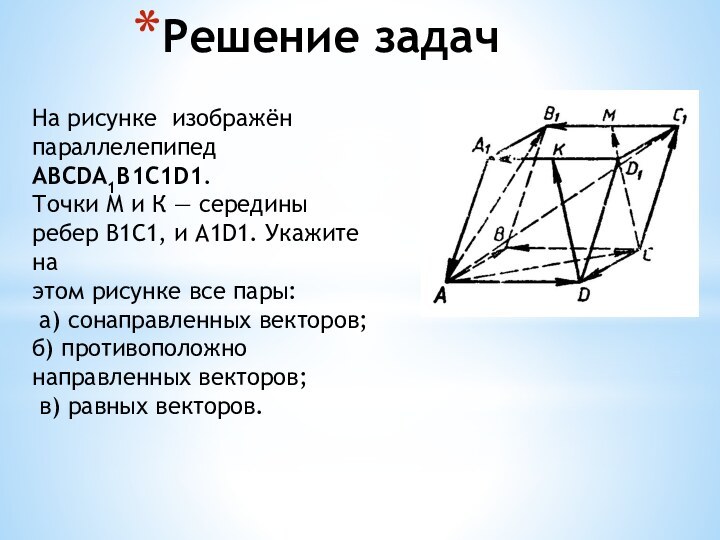
На рисунке изображён параллелепипед ABCDA1B1C1D1.
Точки М
и К — середины ребер В1С1, и A1D1. Укажите
на
этом рисунке все пары:
а) сонаправленных векторов; б) противоположно направленных векторов;
в) равных векторов.
Слайд 8
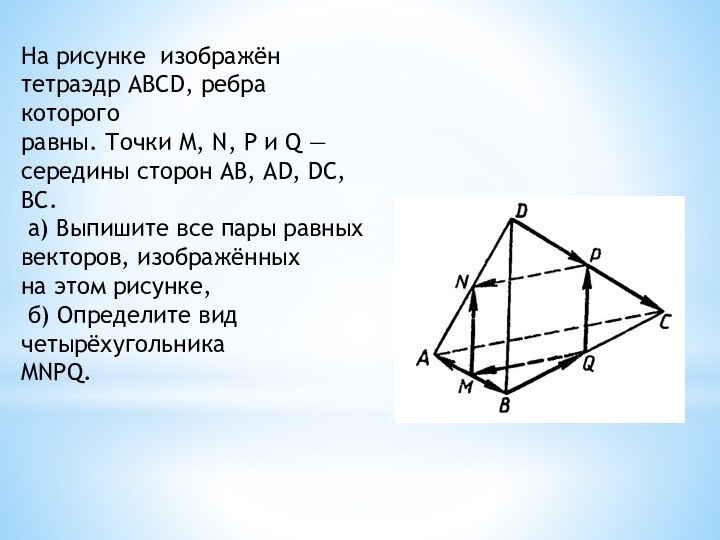
На рисунке изображён тетраэдр ABCD, ребра которого
равны.
Точки М, N, Р и Q — середины сторон
АВ, AD, DC,
ВС.
а) Выпишите все пары равных векторов, изображённых
на этом рисунке,
б) Определите вид четырёхугольника
MNPQ.
Слайд 9
Измерения прямоугольного параллелепипеда ABCDA1B1C1D1 таковы: AD=8 см, AB=9
cм и АА1=12 см. Найдите длины векторов: а) СС1,
СВ, СD; б) DC1, DB, DB1
Слайд 10
Сложение векторов
Сложение двух свободных векторов можно осуществлять как
по правилу параллелограмма, так и по правилу треугольника.
Слайд 11
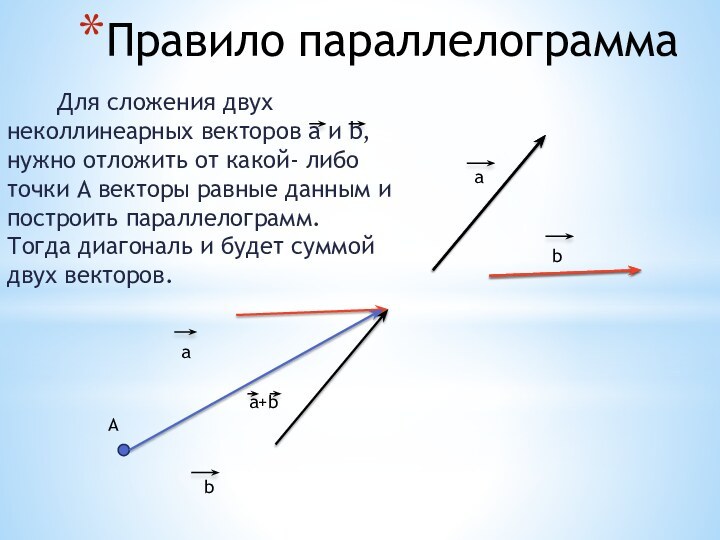
Правило параллелограмма
Для сложения двух
неколлинеарных векторов a и b, нужно отложить от какой-
либо точки А векторы равные данным и построить параллелограмм. Тогда диагональ и будет суммой двух векторов.
a
b
A
a
b
a+b
Слайд 12
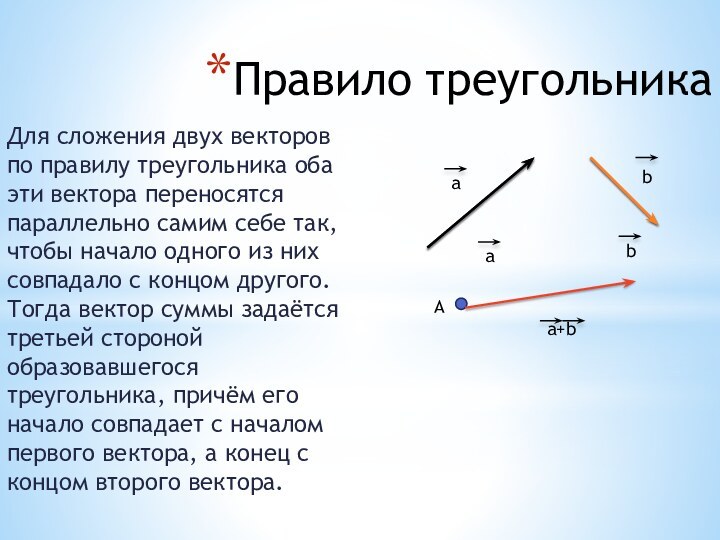
Правило треугольника
Для сложения двух векторов по правилу треугольника
оба эти вектора переносятся параллельно самим себе так, чтобы
начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.
a
b
A
a
b
a+b
Слайд 13
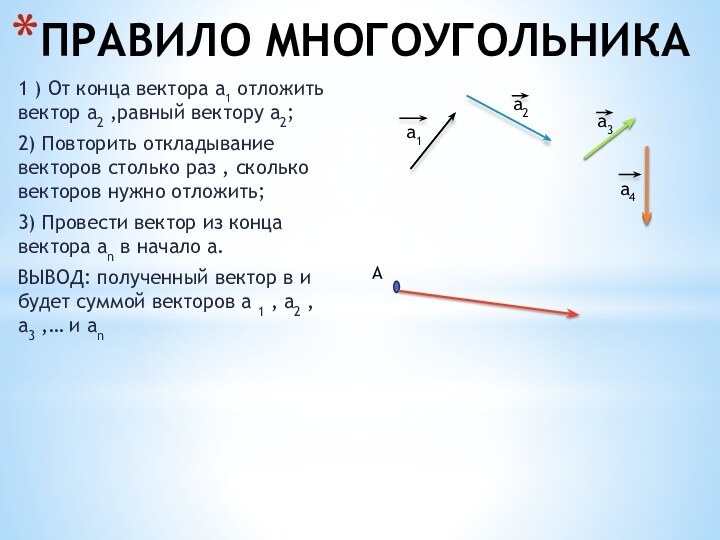
ПРАВИЛО МНОГОУГОЛЬНИКА
1 ) От конца вектора а1
отложить вектор а2 ,равный вектору а2;
2) Повторить откладывание векторов
столько раз , сколько векторов нужно отложить;
3) Провести вектор из конца вектора аn в начало а.
ВЫВОД: полученный вектор в и будет суммой векторов а 1 , а2 , а3 ,… и аn
a1
a2
a3
a4
A
Слайд 14
ЗАКОНЫ СЛОЖЕНИЯ ВЕКТОРОВ
Для любых векторов а , в
и с справедливы равенства:
1) а + b = b
+ а - переместительный закон
2) ( а + b ) + с = а + ( b + с ) -сочетательный закон
Слайд 15
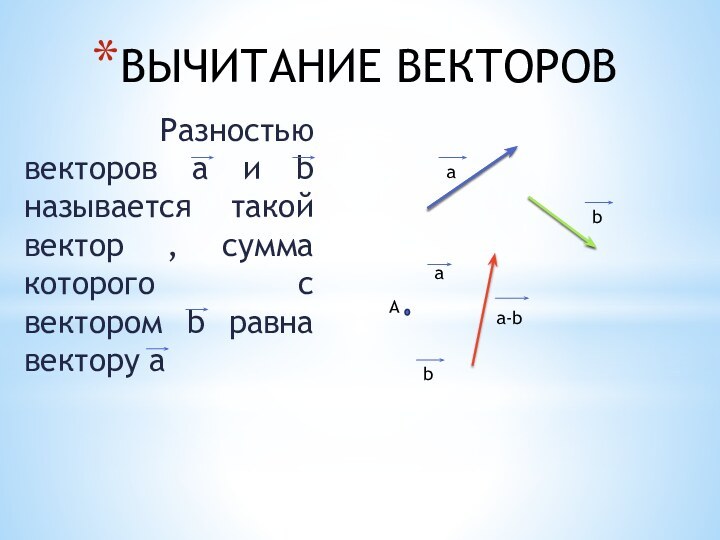
ВЫЧИТАНИЕ ВЕКТОРОВ
Разностью векторов а и
b называется такой вектор , сумма которого с вектором
b равна вектору а
a
b
A
a
b
a-b
Слайд 16
Задачи
используя правило треугольника ,параллелограмма постройте векторы ОА
= а +в
а)
а
b
б)
а
b
с)
b
а
Слайд 17
Задачи
используя треугольника, постройте векторы ОА = а
-в
а)
а
b
б)
а
b
с)
b
а
Слайд 18
Задачи
используя правило треугольника , постройте векторы ОА
= а +в+с
а)
а
b
б)
а
b
с)
b
а
с
с
с
Слайд 21
Умножение вектора на число обладает следующими основными свойствами.
Сочетательный
закон
Первый распределительный закон
Второй распределительный закон
Слайд 24
Задача: Пусть ABCD — параллелограмм, а О —
произвольная точка пространства. Докажите, что: а) ОВ — ОА
= ОС — OD; б) 0B — ОС = DA.
Слайд 25
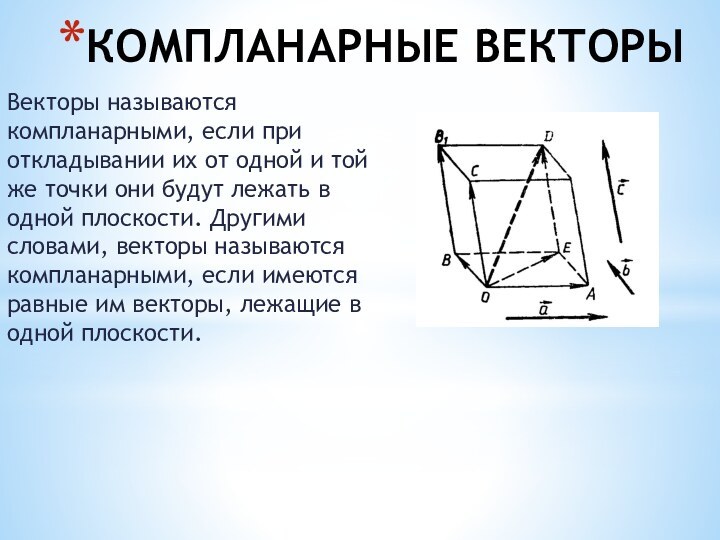
КОМПЛАНАРНЫЕ ВЕКТОРЫ
Векторы называются компланарными, если при откладывании
их от одной и той же точки они будут
лежать в одной плоскости. Другими словами, векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.
Слайд 26
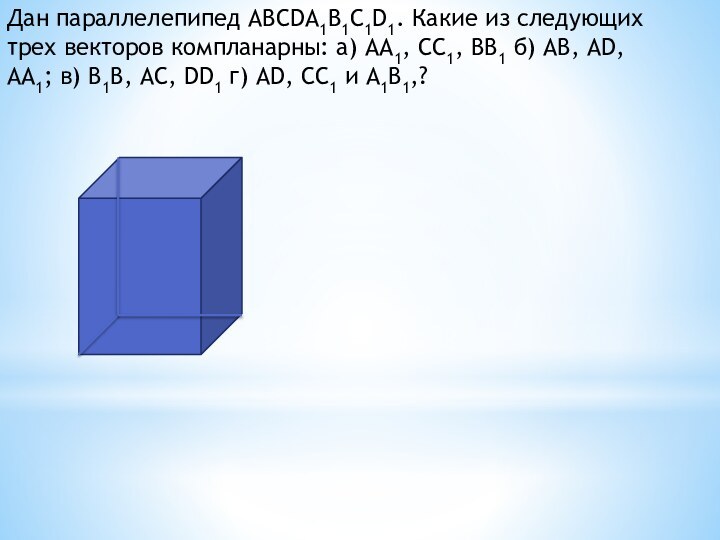
Дан параллелепипед ABCDA1B1C1D1. Какие из следующих
трех векторов
компланарны: а) АА1, СС1, ВВ1 б) АВ, AD,
АА1;
в) В1В, AC, DD1 г) AD, СС1 и А1В1,?
Слайд 27
Если вектор с можно разложить по векторам а
и b, т. е. представить в виде с =
ха + уb, гдe х и у — некоторые числа, то векторы a, b, c компланарны.
Справедливо и обратное утверждение: если векторы а, b и с компланарны, а векторы а и b не коллинеарны, то вектор с можно разложить по векторам а и b, причем коэффициенты разложения (т. е. числа х, у)
определяются единственным образом.
Слайд 28
Правило параллелепипеда.
Для сложения трех некомпланарных векторов можно
пользоваться так называемым правилом параллелепипеда.
Пусть а, Ь, с
— некомпланарные векторы. Отложим от произвольной точки О пространства векторы ОА=а, ОВ=Ь, ОС —с и построим параллелепипед так, чтобы отрезки О А, ОВ и ОС были его ребрами.Тогда диагональ OD этого параллелепипеда изображает сумму векторов а, Ь и с: OD = а + b + c.
Слайд 31
Разложение вектора по трем некомпланарным векторам.
Если вектор
р представлен в виде p = xa + yb
+ zc, где х, у и z — некоторые числа, то говорят, что вектор р разложен по векторам a, b и с. Числа х, у, z называются коэффициентами разложения.
Теорема. Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.