- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему ВОЕННО–МЕДИЦИНСКАЯ АКАДЕМИЯимени С.М. КироваКафедра биологической и медицинской физики
Содержание
- 2. 1. Уравнение гармонического колебанияКолебаниями называют такие процессы,
- 3. Классификация колебаний. 1) По физической природе:
- 4. 5) По характеру взаимодействия с окружающей средой:а)
- 5. Условия возникновения колебаний. а) Наличие
- 6. Математическим маятником называют тело небольших размеров, подвешенное
- 8. В положении равновесия, когда маятник висит по
- 9. Знак «минус» в этой формуле означает, что
- 10. При отклонении маятника он поднимается на определенную
- 11. За счет наличия массы m (масса –
- 12. Уравнение гармонического колебания имеет вид:x(t) = xm cos (ω0 t + φ0),где х
- 13. Величина, стоящая под знаком косинуса φ = ω0t + φ0 называется
- 14. Промежуток времени, через который повторяются определенные состояния
- 15. Частота колебаний ν показывает, сколько колебаний совершается
- 16. Частота колебаний ν связана с циклической частотой
- 17. Графически гармонические колебания можно изображать в виде зависимости х от t и методом векторных диаграмм.
- 19. Метод векторных диаграмм позволяет наглядно представить все
- 20. Если вектор А привести во вращение с
- 21. Время, за которое вектор амплитуды делает один
- 22. 2. Уравнение волны Волны –
- 23. Рассмотрим волну, возникающую на поверхности жидкости под
- 25. Если волна распространяется без затухания, то любая
- 26. Соответственно, фаза колебаний в точке х будет
- 27. Геометрически у волны выделяют следующие элементы:
- 28. Длина волны соответствует расстоянию между соседними гребнями
- 30. 3. Основные характеристики звука. Звук -
- 31. Звуковые волны всегда распространяются в какой-то среде.
- 32. Эти колебания приводят к тому, что в
- 34. Таким образом, звуковая волна – это распространение
- 35. Δр – разность между давлением в данной
- 36. Cкорость распространения звука в воздухе 340 м/c.
- 37. Любая волна переносит в пространстве энергию. Энергетическими
- 38. Поток энергии – средняя энергия, переносимая волнами
- 39. Интенсивность звука (как и любой волны) –
- 40. Так как энергия, переносимая за единицу времени
- 41. Размерность интенсивности = Вт.м-2.Интенсивность можно рассчитать по
- 42. Звуковые методы, используемые в диагностике: а)
- 43. 4. Свойства ультразвука. Ультразвуковые методы исследования
- 44. Для генерирования ультразвука используют ультразвуковые излучатели, основанные
- 45. Прямой пьезоэлектрический эффект
- 46. Обратный пьезоэлектрический эффект
- 47. Свойства ультразвука:1) Ультразвук активно поглощается воздушной средой.
- 48. 2) Скорость распространения УЗ зависит как от
- 49. 3) Ультразвук отражается от границы раздела сред
- 50. Биологические эффекты ультразвука1) Микровибрации на клеточном и
- 51. Медико-биологические приложения ультразвукаДва направления: а) методы диагностики
- 53. Скачать презентацию
- 54. Похожие презентации
1. Уравнение гармонического колебанияКолебаниями называют такие процессы, при которых система с большей или меньшей периодичностью многократно проходит через положение равновесия.












































Слайд 3
Классификация колебаний.
1) По физической природе: механические, электромагнитные, концентрации,
температуры и т.п.
2) По форме: простые (гармонические) и сложные
(являющиеся суммой простых гармонических колебаний).3) По степени периодичности: периодические и апериодические.
4) По характеру изменения во времени: затухающие и незатухающие.
Слайд 4
5) По характеру взаимодействия с окружающей средой:
а) свободные
(однократное поступление энергии в систему извне = однократное внешнее
воздействие);б) вынужденные (многократное (периодическое) поступление энергии в систему извне = периодическое внешнее воздействие);
в) автоколебания (незатухающие колебания в системе с обратной связью, поддерживающиеся за счет имеющейся у системы способности регулировать поступление энергии от постоянного, т.е. непериодического внешнего воздействия).
Слайд 5
Условия возникновения колебаний.
а) Наличие колебательной системы (маятник
на подвесе, пружинный маятник, колебательный контур и т.п.);
б) Наличие
внешнего источника энергии, который способен хотя бы 1 раз вывести систему из положения равновесия;в) Возникновение в системе квазиупругой возвращающей силы (т.е. силы, пропорциональной смещению);
г) Наличие в системе инерции (инерциального элемента).
Слайд 6
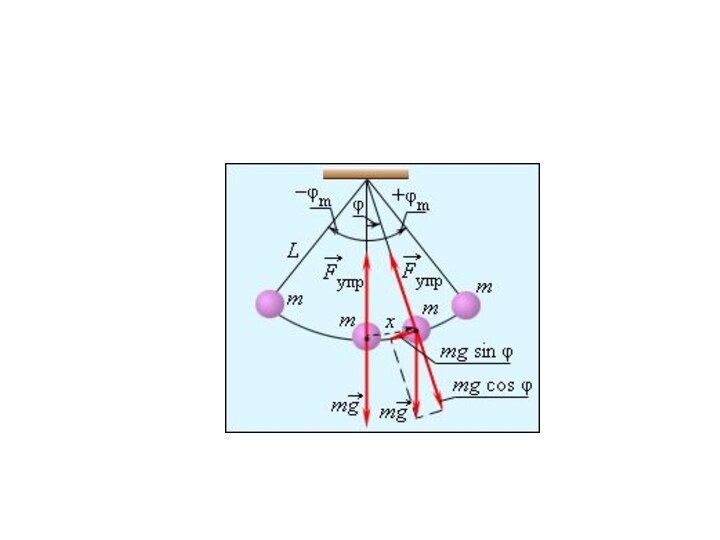
Математическим маятником называют тело небольших размеров, подвешенное на
тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению
с массой тела.Слайд 8 В положении равновесия, когда маятник висит по отвесу,
сила тяжести уравновешивается силой натяжения нити . При отклонении
маятника от положения равновесия на некоторый угол φ появляется касательная составляющая силы тяжестиF=-mg sinφ.
Слайд 9 Знак «минус» в этой формуле означает, что касательная
составляющая направлена в сторону, противоположную отклонению маятника. Она является
возвращающей силой.При небольших углах φ (порядка 15-20о) эта сила пропорциональна смещению маятника, т.е. является квазиупругой, а колебания маятника являются гармоническими.
Слайд 10 При отклонении маятника он поднимается на определенную высоту,
т.е. ему сообщается определенный запас потенциальной энергии (Епот=mgh).
При
движении маятника к положению равновесия происходит переход потенциальной энергии в кинетическую (Eкин =mV2/2).
В момент, когда маятник проходит положение равновесия, потенциальная энергия равна нулю, а кинетическая энергия максимальна.
Слайд 11 За счет наличия массы m (масса – физическая
величина, определяющая инерционные и гравитационные свойства материи) маятник проходит
положение равновесия и отклоняется в противоположном направлении.При отсутствии трения в системе колебания маятника будут продолжаться бесконечно долго (свободные незатухающие колебания).
Слайд 12
Уравнение гармонического колебания имеет вид:
x(t) = xm cos (ω0 t + φ0),
где х –
смещение (отклонение тела от положения равновесия);
xm (А) – амплитуда
колебаний, то есть модуль максимального смещения, ω0 – циклическая (или круговая) частота колебаний,
t – время.
Слайд 13 Величина, стоящая под знаком косинуса φ = ω0t + φ0 называется фазой
гармонического колебания.
Фаза определяет смещение в данный момент времени
t. Фазу выражают в угловых единицах (радианах).
При t = 0 φ = φ0, поэтому φ0 называют начальной фазой.
Слайд 14 Промежуток времени, через который повторяются определенные состояния колебательной
системы, называется периодом колебаний (T).
Физическая величина, обратная периоду
колебаний, называется частотой колебаний:
Слайд 15
Частота колебаний ν показывает, сколько колебаний совершается за
единицу времени.
Единица измерения частоты – герц (Гц) –
одно колебание в секунду. Слайд 16 Частота колебаний ν связана с циклической частотой ω
и периодом колебаний T соотношениями:
То есть круговая частота
- это число полных колебаний, совершающихся за 2π единиц времени.
Слайд 17
Графически гармонические колебания можно изображать в виде зависимости
х от t и методом векторных диаграмм.
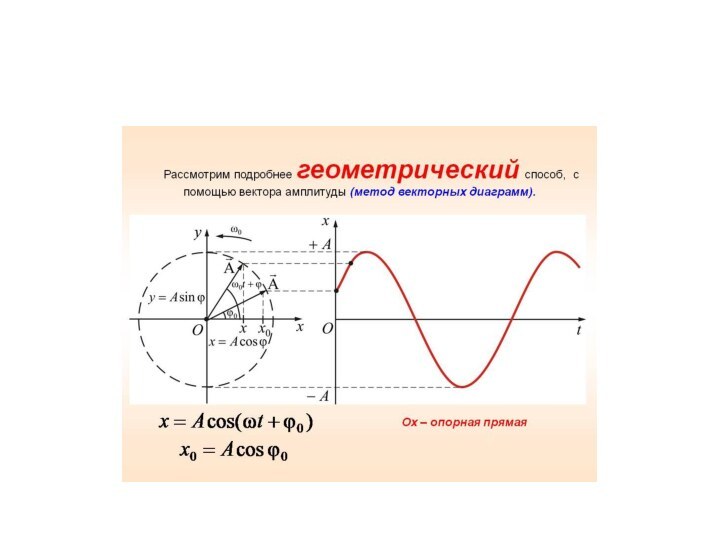
Слайд 19 Метод векторных диаграмм позволяет наглядно представить все параметры,
входящие в уравнение гармонических колебаний.
Действительно, если вектор амплитуды
А расположен под углом φ0 к оси х, то его проекция на ось х будет равна: x = Acos(φ0). Угол φ0 и есть начальная фаза. Слайд 20 Если вектор А привести во вращение с угловой
скоростью ω0, равной круговой частоте колебаний, то проекция конца
вектора будет перемещаться по оси х и принимать значения, лежащие в пределах от -A до +A, причем координата этой проекции будет меняться со временем по закону: x(t) = А cos (ω0 t + φ) .
Слайд 21
Время, за которое вектор амплитуды делает один полный
оборот, равно периоду Т гармонических колебаний.
Число оборотов вектора
в секунду равно частоте колебаний ν.
Слайд 22
2. Уравнение волны
Волны – это колебания, распространяющиеся
в пространстве и переносящие с собой энергию.
Слайд 23 Рассмотрим волну, возникающую на поверхности жидкости под воздействием
колебаний длинного цилиндрического стержня: y(t) = ymax cosωt
где ymax=A
- амплитуда колебаний цилиндра, ω=2πν, где ν - частота колебаний, t - время.
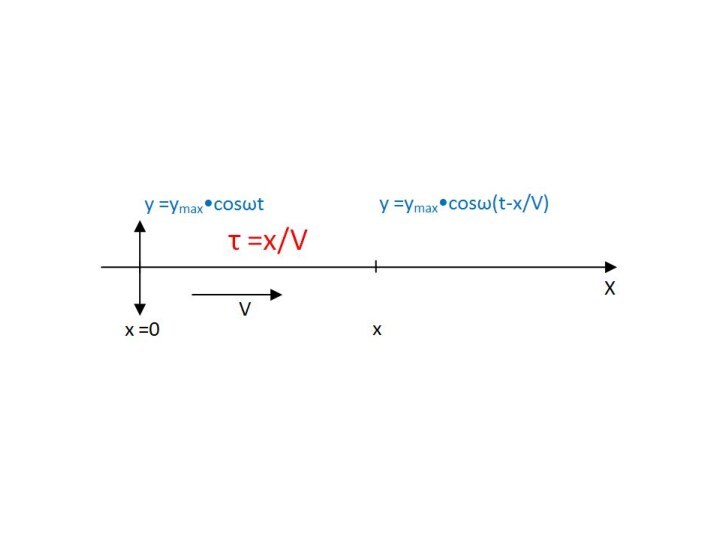
Слайд 25 Если волна распространяется без затухания, то любая точка
поверхности жидкости будет колебаться с той же амплитудой, что
и стержень, но фаза колебаний будет изменяться пропорционально расстоянию от него.Это связано с тем, что волна распространяется с конечной скоростью, и в точку, расположенную на расстоянии x от источника колебаний она придет с временной задержкой τ = x/V.
Слайд 26 Соответственно, фаза колебаний в точке х будет равна
φ=ω(t – τ) = ω(t – x/V),
а уравнение
волны, позволяющее рассчитать состояние системы в любой момент времени в любой точке пространства имеет вид: y(x,t)=ymax сos ω(t – x/v).
Слайд 27
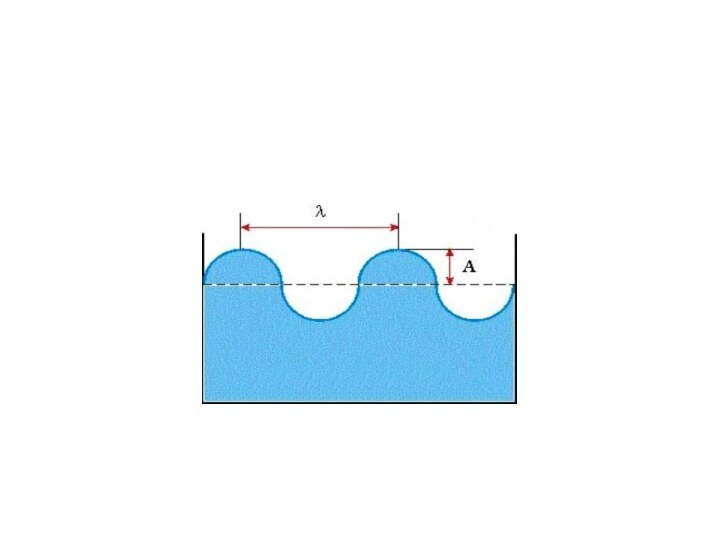
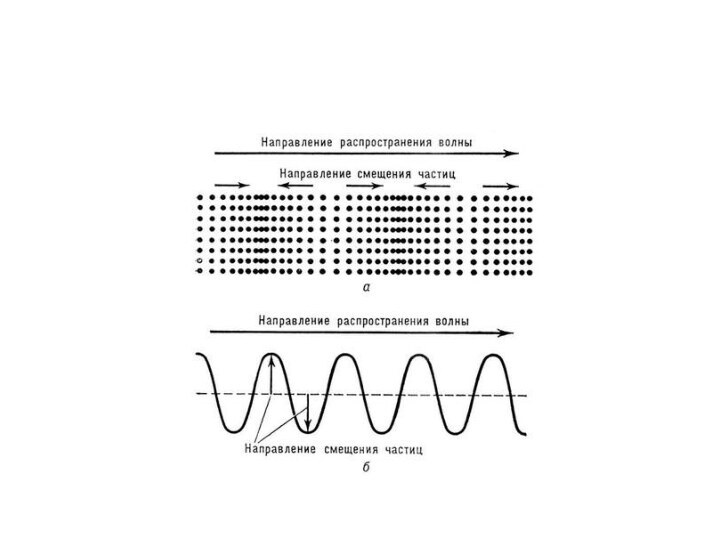
Геометрически у волны выделяют следующие элементы:
гребень волны - множество
точек волны с максимальным положительным отклонением от состояния равновесия;
долина
(ложбина) волны - множество точек волны с наибольшим отрицательным отклонением от состояния равновесия;фронт волны — множество точек, имеющих в некий фиксированный момент времени одинаковую фазу колебаний.
В зависимости от формы фронта волны выделяют плоские, сферические, эллиптические и другие волны.
Слайд 28 Длина волны соответствует расстоянию между соседними гребнями (долинами)
волны.
С другой стороны, длина волны – есть расстояние,
которое волна проходит за один период. Соответственно, λ=VT=V/ν.
Слайд 30
3. Основные характеристики звука.
Звук - это механические
(упругие) колебания, распространяющиеся в газах, жидкостях и твердых телах
(чаще всего в воздухе), которые воспринимаются ухом человека.Для человека границы звукового диапазона соответствуют частотам примерно от 16 Гц до 20 000 Гц.
Некоторые животные ощущают колебания с частотой менее 16 Гц (инфразвуки); другие (летучие мыши, дельфины) – с частотами много выше 20 000 Гц (ультразвуки).
Слайд 31
Звуковые волны всегда распространяются в какой-то среде.
В
газах и жидкостях эти волны продольные, то есть молекулы
среды колеблются вдоль направления распространения волны.Слайд 32 Эти колебания приводят к тому, что в одних
точках возникает сгущение молекул, приводящее к локальному повышению давления,
а в других точках - разрежение (понижение давления).Слайд 34 Таким образом, звуковая волна – это распространение в
воздухе (или в другой среде) колебаний давления.
В простейшем
случае эти колебания могут быть гармоническими (в музыке такие колебания называют чистыми тонами).Гармоническое звуковое колебание выражается формулой:
Δр = Δрmax.cos ω(t – x/V)
Слайд 35
Δр – разность между давлением в данной точке
волны и давлением в невозмущённой среде (практически – атмосферным
давлением).Величину Δр называют звуковым давлением.
Слайд 36
Cкорость распространения звука в воздухе 340 м/c.
Поэтому
при частоте 20 Гц длина волны равна λ =
VT = V/? =340/20 = 17 м;при частоте 20 000 Гц - в 1000 раз меньше, то есть 17 мм.
Как видно, длина звуковых волн сравнима с размерами окружающих нас предметов, поэтому для звука большое значение имеет дифракция, то есть звуковые волны огибают встречающиеся на их пути предметы.
Слайд 37
Любая волна переносит в пространстве энергию.
Энергетическими характеристиками
звука (как и любой другой волны) являются поток энергии
и интенсивность (плотность потока энергии).Слайд 38 Поток энергии – средняя энергия, переносимая волнами в
единицу времени через некоторую поверхность.
? = Е/t
Усреднение производят за
время, значительно превышающее период колебаний.Единица измерения потока – ватт
(1 Вт = 1 Дж/с).
Слайд 39
Интенсивность звука (как и любой волны) – это
физическая величина, равная энергии, переносимой волной через единичную площадку,
перпендикулярную направлению распространения волны, за единицу времени.Слайд 40 Так как энергия, переносимая за единицу времени –
это поток энергии, то интенсивность – это плотность потока
энергии, т.е. поток энергии, приходящийся на единицу площади, ориентированной перпендикулярно направлению распространения волн:
Слайд 41
Размерность интенсивности = Вт.м-2.
Интенсивность можно рассчитать по формуле:
I
= ρA2ω2V/2
Интенсивность звука связана простым соотношением со звуковым давлением:
I = Δpmax / (2ρV),
где ρ – плотность среды, V – скорость звука.
Слайд 42
Звуковые методы, используемые в диагностике:
а) Аускультация – выслушивание
звуков, возникающих при работе различных органов (сердца, легких, кровеносных
сосудов) в норме и патологии с диагностическими целями (с этой целью используют стетоскоп, фонендоскоп, микрофон, магнитофон).б) Фонокардиография – графическая регистрация тонов и шумов сердца.
в) Перкуссия – прослушивание звучания отдельных частей тела при простукивании. При ударе о поверхность тела возникает звуковая волна. Во внутритканных полостях возникают резонансные явления, которые изменяют тембр и громкость звучания. Опытный врач по изменению звучания определяет состояние обследуемого органа (воспаление в мягких тканях, наличие жидкости в брюшной полости и т.п.)
Слайд 43
4. Свойства ультразвука. Ультразвуковые методы исследования
Ультразвук – это
механические волны, распространяющиеся в упругих средах и имеющие частоту
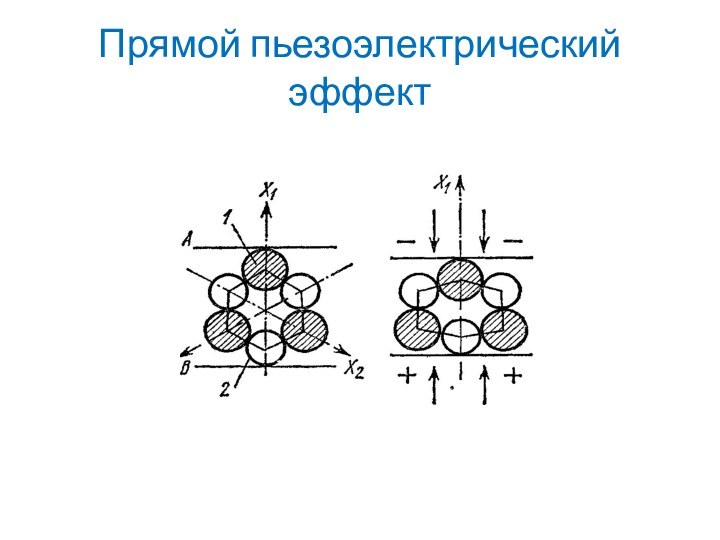
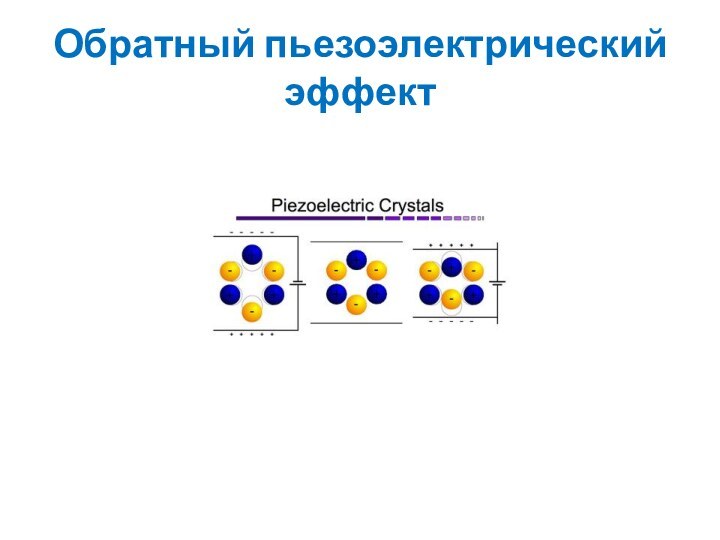
свыше 20 кГц (до 109 -1010 Гц).Слайд 44 Для генерирования ультразвука используют ультразвуковые излучатели, основанные на
явлении обратного пьезоэлектрического эффекта (деформация кристаллов при наложении на
них электрического поля).Такими свойствами обладают кварц, сегнетова соль, керамика на основе титаната бария.
Приемник УЗ основан на прямом пъезоэлектрическом эффекте (появление разности потенциалов на гранях кристалла при его деформации).
Слайд 47
Свойства ультразвука:
1) Ультразвук активно поглощается воздушной средой.
На
расстоянии 12 см интенсивность УЗ-волны в воздухе уменьшается в
10 раз (в воде это расстояние почти в 3000 раз больше).Слайд 48 2) Скорость распространения УЗ зависит как от среды,
в которой он распространяется, так и от состояния этой
среды (температура, давление, влажность).В воздухе скорость распространения УЗ – 330 м/с, в воде – 1500 м/с, в костных тканях – около 3370 м/с.
Слайд 49 3) Ультразвук отражается от границы раздела сред с
разным акустическим сопротивлением (так, на границе «вода-воздух» отражается более
90% ультразвуковой энергии).4) УЗ-волна обладает достаточно большой энергией (механические разрушения, тепловой эффект).
5) Распространение ультразвука в газах и жидкостях сопровождается такими явлениями, как осаждение суспензий, коагуляция аэрозолей, кавитация.
Слайд 50
Биологические эффекты ультразвука
1) Микровибрации на клеточном и субклеточном
уровне.
2) Разрушение биомакромолекул.
3) Перестройка и повреждение биомембран, изменение их
проницаемости.4) Тепловой эффект.
5) Разрушение клеток и микроорганизмов.





























