Слайд 2
0. Введение.
Общие сведения.
Объем курса – 18 часов
лекции
16 часов лабораторные занятия
Лабораторные занятия проводятся в классе ПЭВМ
и выполняются в среде пакета R
Форма отчетности – зачет
Лектор – Воротницкая Татьяна Ивановна
Слайд 3
0. Введение.
Что такое компьютерный анализ данных
Компьютерный анализ
данных - научное направление, объединяющее вероятностно-статистические, логико-алгебраические, графические, другие
модели, а также алгоритмы, программные средства обработки и анализа эмпирических данных с целью получения научно-обоснованных выводов и принятия решений относительно исследуемых объектов
Слайд 4
0. Введение.
Основные разделы
Статистический анализ данных (Statistical
Data Analysis – SDA)
Интеллектуальный анализ данных (Data Mining
или Knowledge Discovery in Database - KDD)
Анализ больших данных (Big Data Analysis - BDA)
Слайд 5
0. Введение.
Литература.
Ширяев А.Н. Вероятность. Москва, 1980.
Вентцель Е.С.
Теория вероятностей: Учеб. для вузов. — 6-е изд. стер.
— М.: Высш. шк., 1999.
Колмогоров А.Н. Основные понятия теории вероятностей. Москва, 1936.
Хацкевич Г.А. Статистика. Описательный подход / Г.А. Хацкевич. – Минск: НИУП. – 2002.
А. А. Барсегян, М. С. Куприянов, В. В. Степаненко, И. И. Холод Технологии анализа данных. Data Mining, Visual Mining, Text Mining, OLAP
Елисеева И.И. Общая теория статистики / И.И. Елисеева, М.М. Юзбашев. – М. – 1996.
Тюрин Ю.Н. Анализ данных на компьютере / Ю.Н. Тюрин, А.А. Макаров
Torgo L. Data Mining with R: learning by case studies / L. Torgo - LIACC-FEP, University of Porto. – 2003.
Слайд 6
1. Основные понятия теории вероятностей
Теория вероятностей - математическая
наука, изучающая закономерности в случайных явлениях
Случайное явление –
это такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по-иному
Слайд 7
1. Основные понятия теории вероятностей
Примеры случайных явлений
Стрельба из
орудия, установленного под заданным углом к горизонту
Детерминированы: начальная скорость
снаряда, угол бросания, форма снаряда
Фактическая траектория снаряда отклоняется за счет совокупного влияния второстепенных случайных факторов: ошибки изготовления снаряда, отклонение веса порохового заряда от номинала, неоднородность структуры и неравномерность горения заряда, ошибки установки ствола, вариации атмосферного давления и др.
Слайд 8
1. Основные понятия теории вероятностей
Примеры случайных явлений
Взвешивание одного
и того же тела на аналитических весах
Детерминированы: массы тела
и разновесов, геометрические форма и размеры плеч весов, значение ускорения свободного падения
Результаты повторных взвешиваний несколько отличаются за счет совокупного влияния второстепенных случайных факторов: положения тела на чашке весов, случайные вибрации, ошибки отсчета показаний прибора и др.
Слайд 9
1. Основные понятия теории вероятностей
Примеры случайных явлений
Бросание игральной
кости
Детерминированы: форма (куб) и распределение плотности материала (в идеале
– равномерное)
Результаты повторных выбрасываний отличаются за счет случайных направлений и скоростей поступательного и вращательного движений при бросании кости
Слайд 10
1. Основные понятия теории вероятностей
Какие закономерности изучает теория
вероятностей
Теория вероятностей изучает закономерности, проявляющиеся при рассмотрении большого числа
однородных случайных явлений.
Закономерности, проявляющиеся в массе случайных явлений нивелируют, «погашают» индивидуальные особенности каждого из случайных явлений.
Методы теории вероятностей по природе приспособлены только для исследования массовых случайных явлений; они не дают возможности предсказать исход отдельного случайного явления, но дают возможность предсказать средний суммарный результат массы однородных случайных явлений, предсказать средний исход массы аналогичных опытов, конкретный исход каждого из которых остается неопределенным, случайным.
Слайд 11
1. Основные понятия теории вероятностей
Событие
Под «событием» в теории
вероятностей понимается всякий факт, который в результате опыта может
произойти или не произойти.
Примеры событий:
Появление герба при однократном бросании монеты
появление трех гербов при трехкратном бросании монеты;
попадание в цель при выстреле;
появление туза при вынимании карты из колоды;
обнаружение объекта при одном цикле обзора радиолокационной станции;
обрыв нити в течение часа работы ткацкого станка.
Каждое событие обладает различной степенью возможности.
С каждым событием можно попытаться связать некоторое число, характеризующее объективную возможность события – вероятность.
Единица измерения вероятностей вероятность достоверного события = 1. Вероятность невозможного события = 0.
Слайд 12
1. Основные понятия теории вероятностей
Статистическая устойчивость
Если А –
некоторое случайное событие, то доля m/n экспериментов, в которых
данное событие произошло, имеет тенденцию стабилизироваться с ростом общего числа экспериментов n, приближаясь к некоторому числу p(A). Это число служит объективной характеристикой «степени возможности» произойти событию А
Пример: эксперимент по бросанию монеты.
Случайное событие – выпадение герба
Проведем по 10 экспериментов, в каждом из которых будем проводить n испытаний, n=102, 104, 106.
Число выпадений герба в каждой серии обозначим m.
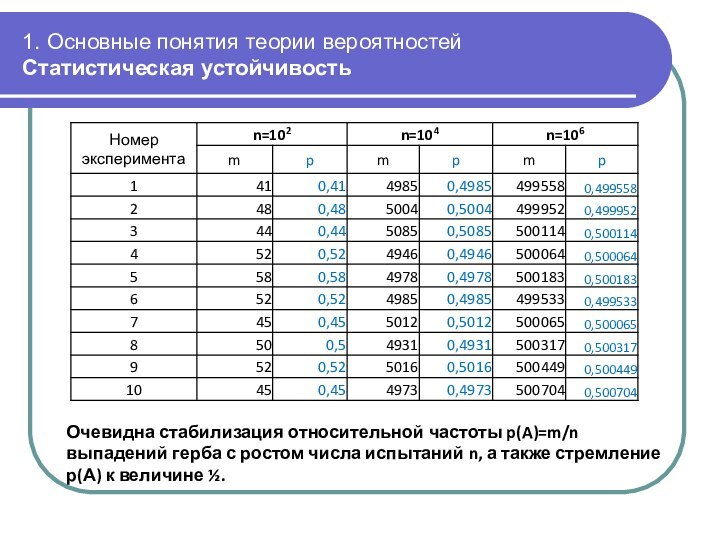
В таблице показаны значения m в каждом из экспериментов и значения относительной частоты p(A)=m/n выпадений герба при различном числе испытаний
Слайд 13
1. Основные понятия теории вероятностей
Статистическая устойчивость
Очевидна стабилизация относительной
частоты p(A)=m/n выпадений герба с ростом числа испытаний n,
а также стремление р(А) к величине ½.
Слайд 14
1. Основные понятия теории вероятностей.
Пространство элементарных исходов.
Пространством элементарных
событий называется множество, содержащее все возможные случайные результаты
данного эксперимента, из которых в эксперименте происходит ровно один. Элементы этого множества называют элементарными исходами .
Событиями будем называть подмножества множества . Говорят, что в результате эксперимента произошло событие А, если в эксперименте произошел один из элементарных исходов, входящих в множество А.
Слайд 15
1. Основные понятия теории вероятностей.
Пространство элементарных исходов.
Пример: однократное
подбрасывание игральной кости.
Пространством элементарных событий = {1,2,3,4,5,6}.
Элементарное
событие – число выпавших очков
Примеры событий: А={1,2} – выпало одно или два очка; B={1,3,5} – выпало нечетное число очков.
Достоверным называется событие, которое обязательно происходит в результате эксперимента, т.е. единственное событие, включающее все элементарные исходы
Невозможным называется событие, которое не может произойти в результате эксперимента, т.е. событие не содержащее ни одного элементарного исхода – пустое множество.
Слайд 16
1. Основные понятия теории вероятностей.
Вероятность на дискретном пространстве
элементарных исходов
Слайд 17
1. Основные понятия теории вероятностей.
Свойства вероятности на дискретном
пространстве элементарных исходов
Слайд 18
1. Основные понятия теории вероятностей.
Классическое определение вероятности
Слайд 19
1. Основные понятия теории вероятностей.
Классическое определение вероятности
Слайд 20
1. Основные понятия теории вероятностей.
Вероятность и частота
Слайд 21
1. Основные понятия теории вероятностей.
Геометрическое определение вероятности
Для испытаний
с бесконечным числом исходов классическое определение вероятности неприменимо.
Тогда вводят
понятие геометрической вероятности, как вероятности попадания точки в область (отрезок, часть плоскости, часть n-мерного пространства).
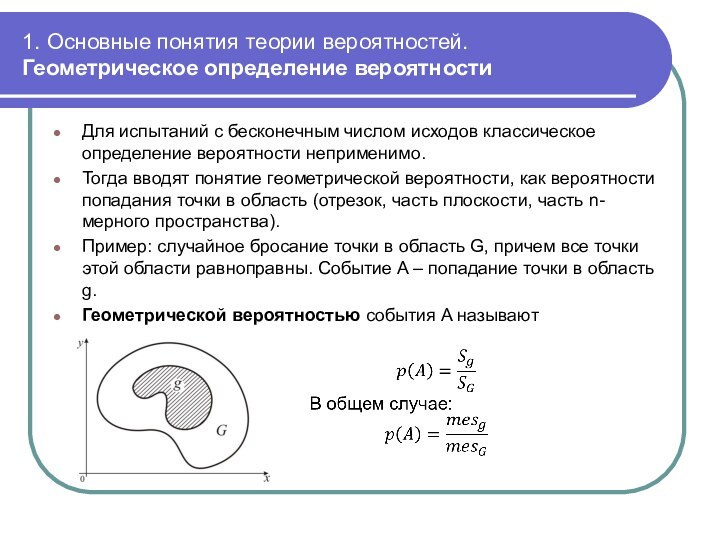
Пример: случайное бросание точки в область G, причем все точки этой области равноправны. Событие A – попадание точки в область g.
Геометрической вероятностью события A называют
Слайд 22
1. Основные понятия теории вероятностей.
Геометрическое определение вероятности
Пример.
Два
студента A и B условились встретиться в определенном месте
во время перерыва между 13 ч и 13 ч 50 мин. Пришедший первым ждет другого в течение 10 мин., после чего уходит. Чему равна вероятность их встречи, если приход каждого из них в течение указанных 50 минут может произойти наудачу и моменты прихода независимы?
Слайд 23
1. Основные понятия теории вероятностей.
Условная вероятность
Пример. Игральная кость
подбрасывается один раз. Известно, что выпало более трех очков.
Какова при этом вероятность, что выпало четное число очков?
Решение
а) = {4,5,6}, A={4,6}. p(A)=2/3.
б) = {1,2,3,4,5,6}; B = {4,5,6}. Вопрос: какова вероятность того, что при осуществлении B происходит А ={4,6}: p(A|B) ?
p(A|B) = p(A ∩ B)/P(B) =(2/6)/(3/6)=2/3.
Условной вероятностью события A по отношению к событию B p(A|B) называют вероятность события A, найденную при условии, что произошло событие B
Слайд 24
1. Основные понятия теории вероятностей.
Правило умножения вероятностей событий
Правило
умножения вероятностей: Вероятность произведения двух событий равна произведению вероятности
одного из этих событий на условную вероятность другого, найденную в предположении, что первое событие произошло, т.е. p(AB)=p(A)p(B|A) или p(AB)=p(B)p(A|B)
События A и B называются независимыми, если p(A|B) = p(A) и p(B|A) = p(B). Для независимых событий p(AB)=p(A)p(B).
Пример. В первом ящике 2 белых и 10 красных шаров, во втором ящике – 8 белых и 4 красных. Из каждого ящика вынули по шару. Какова вероятность, что оба шара белые?
Решение. A={появление белого шара из первого ящика}, B={появление белого шара из второго ящика}. A и B – независимы. p(AB)=p(A)p(B)=2/12 8/12 = 1/9
Слайд 25
1. Основные понятия теории вероятностей.
Формула полной вероятности
Слайд 26
1. Основные понятия теории вероятностей.
Формула полной вероятности
Пример. Имеется
четыре одинаковых ящика с электрическими лампочками, причем первый ящик
содержит 10 исправных и 2 бракованные лампочки, второй и третий ящики содержат по 5 исправных и по 5 бракованных лампочек, а четвертый ящик содержит только 10 исправных лампочек. Наудачу выбирается один ящик и из него одна лампочка. Какова вероятность того, что эта лампочка окажется исправной?
Решение. Событие A={выбор исправной лампочки}. Гипотезы Bi={выбор i-го ящика}. События Bi образуют полную группу событий, p(Bi)=1/4. p(A|B1)=10/12=5/6; p(A|B2)= p(A|B3)=5/10=1/2; p(A|B4)=10/10=1. Тогда по формуле полной вероятности
p(A)=p(B1)p(A|B1)+ p(B2)p(A|B2)+ p(B3)p(A|B3)+ p(B4)p(A|B4) = 1/4 5/6+ 1/4 1/2+ 1/4 1/2+ 1/4 1=17/24
Слайд 27
1. Основные понятия теории вероятностей.
Формула Байеса
Слайд 28
2. Случайные величины и их характеристики
Понятие случайной величины
Случайной
величиной называется величина которая в результате опыта принимает то
или иное числовое значение, причем заранее, до опыта, неизвестно, какое именно.
Дискретные случайные величины принимают конечное или счетное множество значений. Примеры: число попаданий в цель при трех выстрелах, число вызовов, поступавших на телефонную станцию за сутки.
Случайные величины, значения которых непрерывно заполняют некоторый промежуток (конечный или бесконечный) числовой оси называют непрерывными. Примеры: скорость космического аппарата при выходе на орбиту, ошибка взвешивания тела на аналитических весах.
Современная теория вероятностей предпочитает оперировать не с событиями, а с соответствующими им случайными величинами.
1
0
Слайд 29
2. Случайные величины и их характеристики
Закон распределения
Законом распределения
случайной величины называется всякое соотношение, устанавливающее связь между возможными
значениями случайной величины и соответствующими им вероятностями.
Закон распределения может быть задан аналитически, графически, для дискретной случайной величины – в виде таблицы:
Слайд 30
2. Случайные величины и их характеристики
Функции распределения случайных
величин
0
x
X
p
Слайд 31
2. Случайные величины и их характеристики
Свойства функции распределения
0
a
x
b
F
Слайд 32
2. Случайные величины и их характеристики
Плотность распределения непрерывной
случайной величины
dx
f(x)
f(x)
a
b
Слайд 33
2. Случайные величины и их характеристики
Дискретное равномерное распределение
f
F
Слайд 34
2. Случайные величины и их характеристики
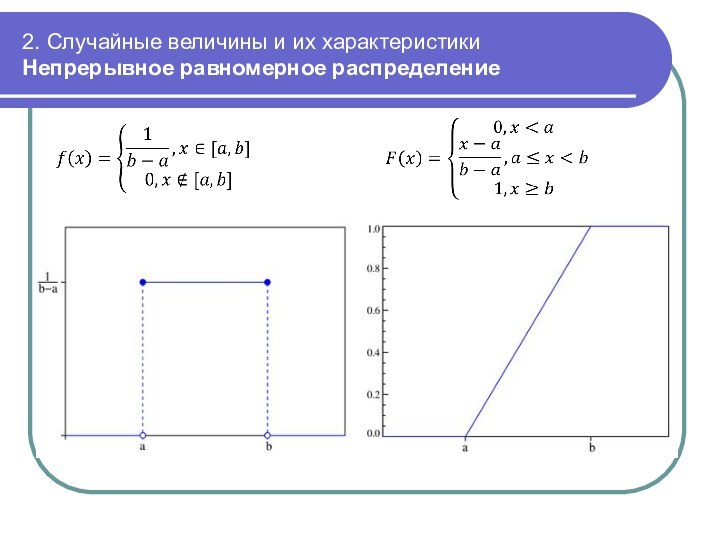
Непрерывное равномерное распределение
Слайд 35
2. Случайные величины и их характеристики
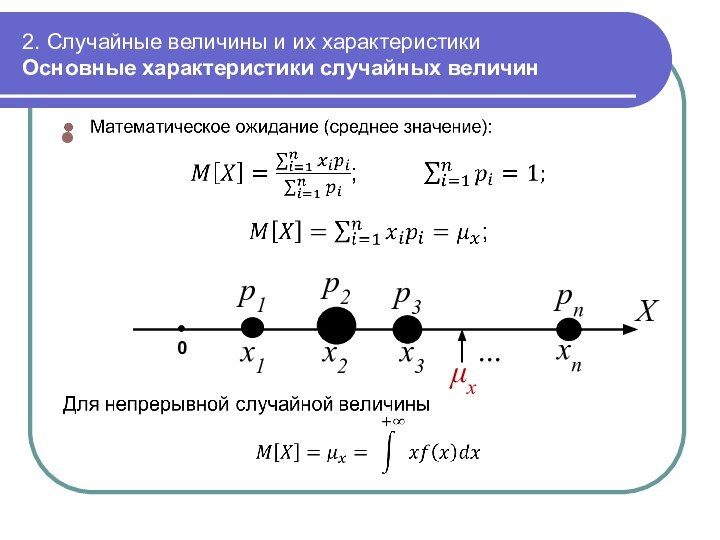
Основные характеристики случайных
величин
0
x1
X
p1
x2
x3
xn
…
p2
p3
pn
μx
Слайд 36
2. Случайные величины и их характеристики
Основные характеристики случайных
величин
Слайд 37
2. Случайные величины и их характеристики
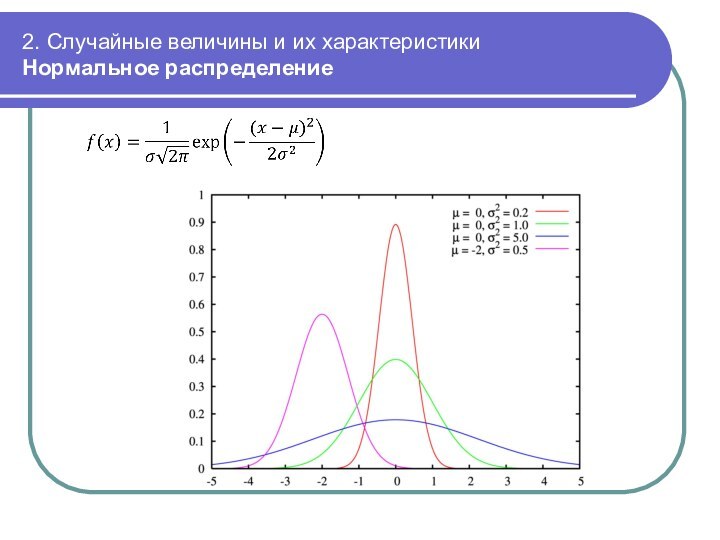
Нормальное распределение
Слайд 38
2. Случайные величины и их характеристики
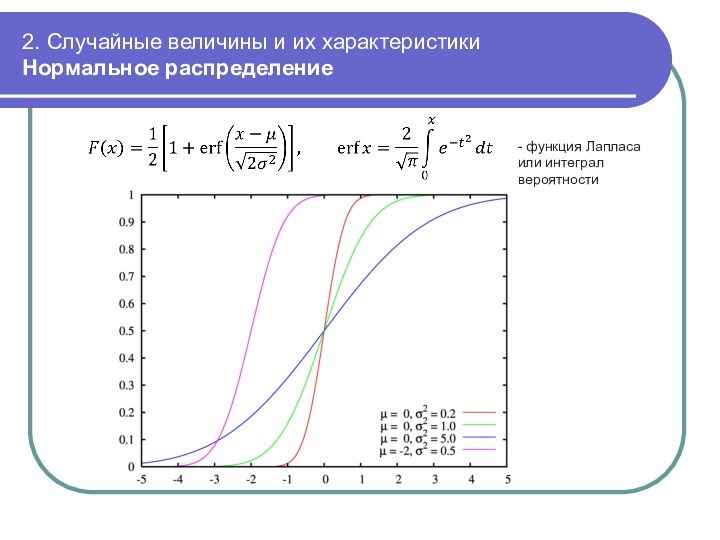
Нормальное распределение
-
функция Лапласа или интеграл вероятности
Слайд 39
2. Случайные величины и их характеристики
Понятие случайного процесса
0
t
t1
t2
Слайд 40
2. Случайные величины и их характеристики
Основные задачи статистики
Предмет
математической статистики – разработка методов регистрации, описания и анализа
статистических экспериментальных данных, получаемых в результате наблюдения массовых случайных явлений.
Основные задачи математической статистики:
Задача определения закона распределения случайной величины (или системы случайных величин) по статистическим данным
Задача проверки правдоподобия гипотез
Задача нахождения неизвестных параметров распределения
«There are three kinds of lies: lies, damned lies, and statistics.»
Приписывается премьер-министру Великобритании Бенджамину Дизраэли.
Слайд 41
2. Случайные величины и их характеристики
Генерация псевдослучайных последовательностей
Источники
настоящих последовательностей случайных чисел – случайные природные процессы: оптические
квантовые эффекты (отражение фотонов от полупрозрачного зеркала), радиоактивный распад, дробовой шум в радиоэлектронных приборах за счет дискретности носителей тока, детектирование космического излучения и т.п.).
Компьютер – детерминированная система. С его помощью можно генерировать только псевдослучайные последовательности.
Слайд 42
2. Случайные величины и их характеристики
Генерация псевдослучайных последовательностей
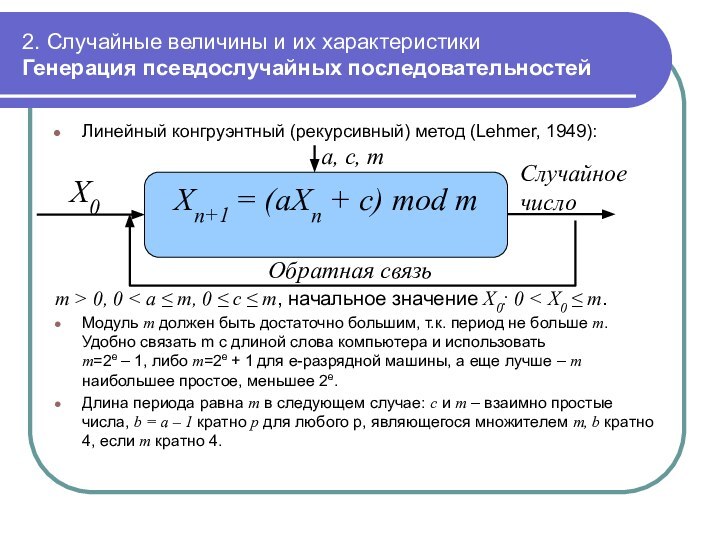
Линейный
конгруэнтный (рекурсивный) метод (Lehmer, 1949):
m > 0, 0
a ≤ m, 0 ≤ c ≤ m, начальное значение X0: 0 < X0 ≤ m.
Модуль m должен быть достаточно большим, т.к. период не больше m. Удобно связать m с длиной слова компьютера и использовать
m=2e – 1, либо m=2e + 1 для e-разрядной машины, а еще лучше – m наибольшее простое, меньшее 2e.
Длина периода равна m в следующем случае: c и m – взаимно простые числа, b = a – 1 кратно p для любого p, являющегося множителем m, b кратно 4, если m кратно 4.
Xn+1 = (aXn + c) mod m
X0
Случайное число
Обратная связь
a, c, m
Слайд 43
2. Случайные величины и их характеристики
Генерация псевдослучайных последовательностей
Генератор
MS FORTRAN: m = 231-1, c=0, a=48271
Xn+1 = 48271Xn
mod (231-1)
Генератор Парка-Миллера: m = 231-1, c=0, a=75
Xn+1 = 75Xn mod (231-1)
Нелинейные генераторы:
Xn+1 = (aXn3 + bXn2 + cXn +d)mod m
Суперпозиция нескольких конгруэнтных генераторов посредством нелинейной функции.
Слайд 44
2. Случайные величины и их характеристики
Генерация псевдослучайных последовательностей
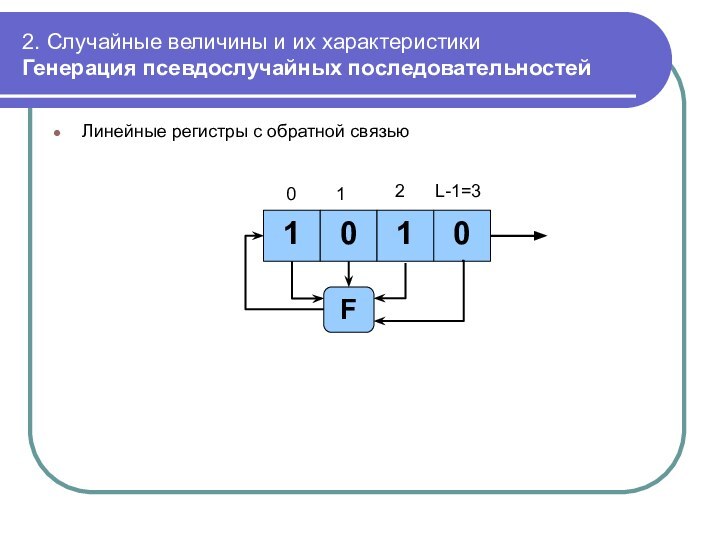
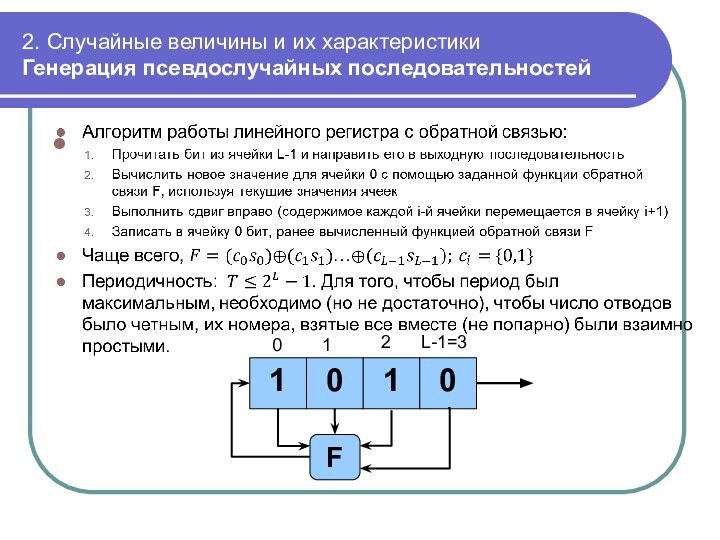
Линейные
регистры с обратной связью
1
0
1
0
0
1
2
L-1=3
F
Слайд 45
2. Случайные величины и их характеристики
Генерация псевдослучайных последовательностей
1
0
1
0
0
1
2
L-1=3
F
Слайд 46
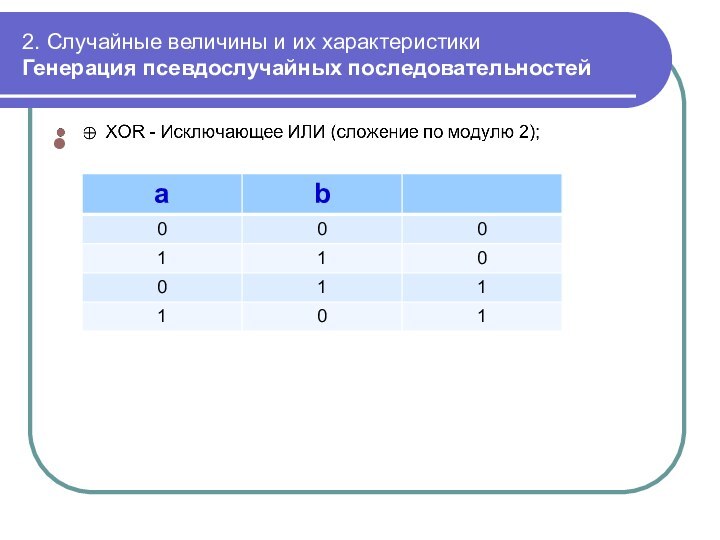
2. Случайные величины и их характеристики
Генерация псевдослучайных последовательностей
Слайд 47
2. Случайные величины и их характеристики
Генерация псевдослучайных последовательностей
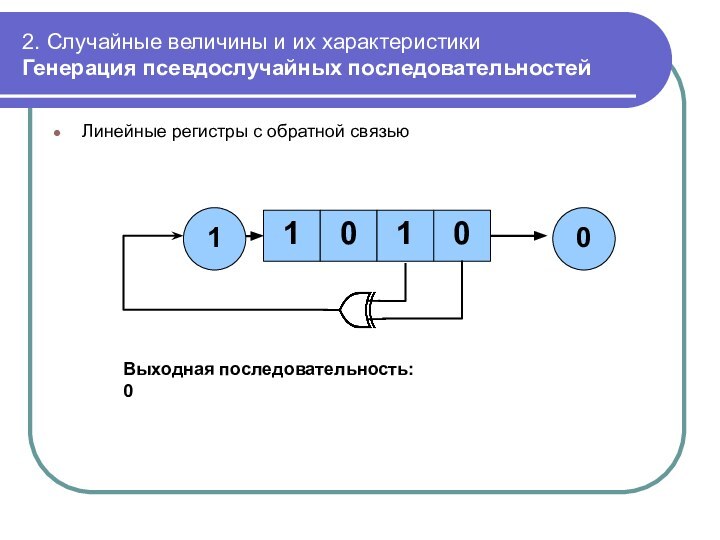
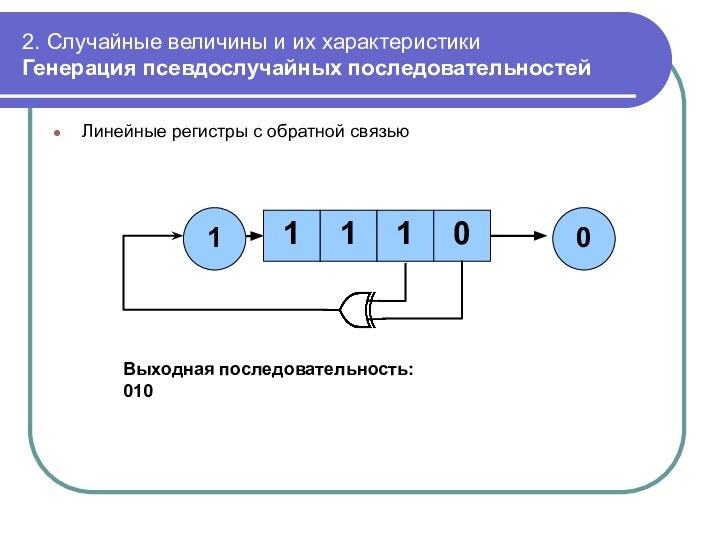
Линейные
регистры с обратной связью
1
0
1
0
0
1
Выходная последовательность:
0
Слайд 48
2. Случайные величины и их характеристики
Генерация псевдослучайных последовательностей
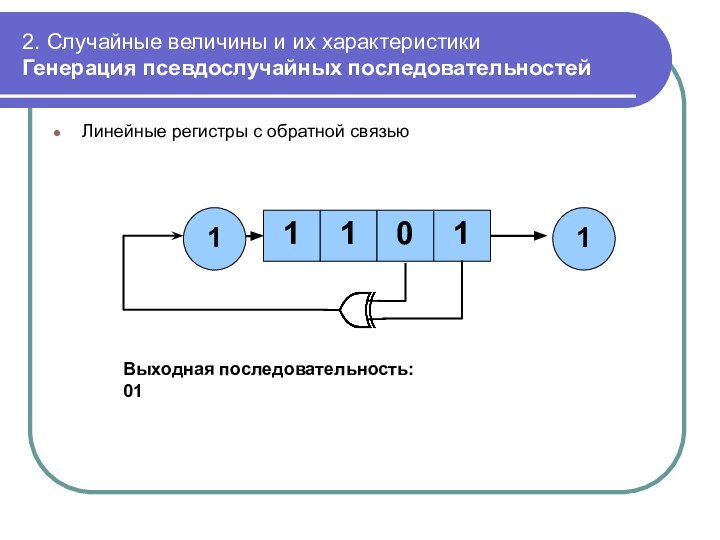
Линейные
регистры с обратной связью
1
1
0
1
1
1
Выходная последовательность:
01
Слайд 49
2. Случайные величины и их характеристики
Генерация псевдослучайных последовательностей
Линейные
регистры с обратной связью
1
1
1
0
0
1
Выходная последовательность:
010
Слайд 50
2. Случайные величины и их характеристики
Генерация псевдослучайных последовательностей
Линейные
регистры с обратной связью
1
1
1
1
1
0
Выходная последовательность:
0101
Слайд 51
2. Случайные величины и их характеристики
Генерация псевдослучайных последовательностей
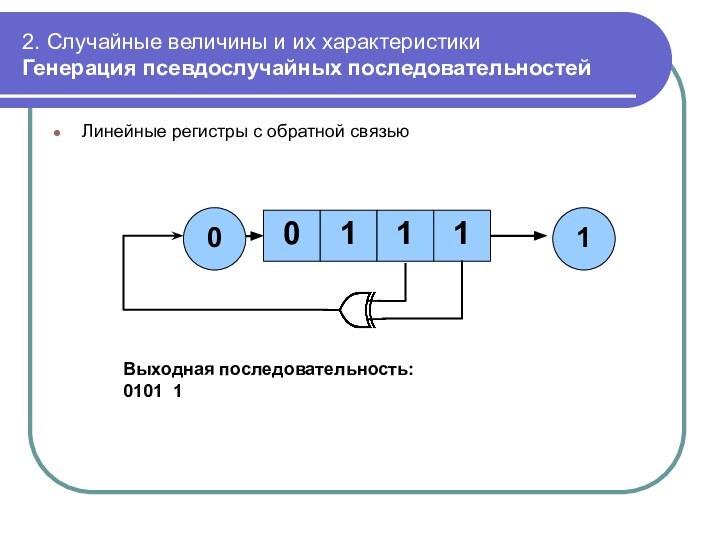
Линейные
регистры с обратной связью
0
1
1
1
1
0
Выходная последовательность:
0101 1
Слайд 52
2. Случайные величины и их характеристики
Генерация псевдослучайных последовательностей
Линейные
регистры с обратной связью
0
0
1
1
1
0
Выходная последовательность:
0101 11
Слайд 53
2. Случайные величины и их характеристики
Генерация псевдослучайных последовательностей
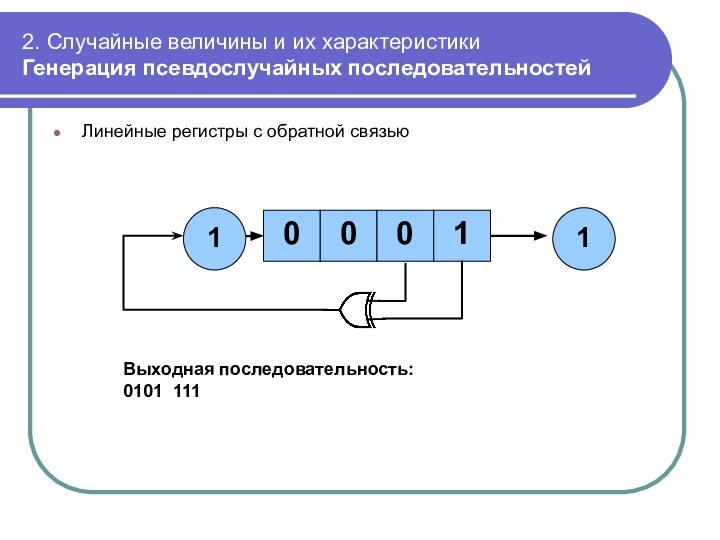
Линейные
регистры с обратной связью
0
0
0
1
1
1
Выходная последовательность:
0101 111
Слайд 54
2. Случайные величины и их характеристики
Генерация псевдослучайных последовательностей
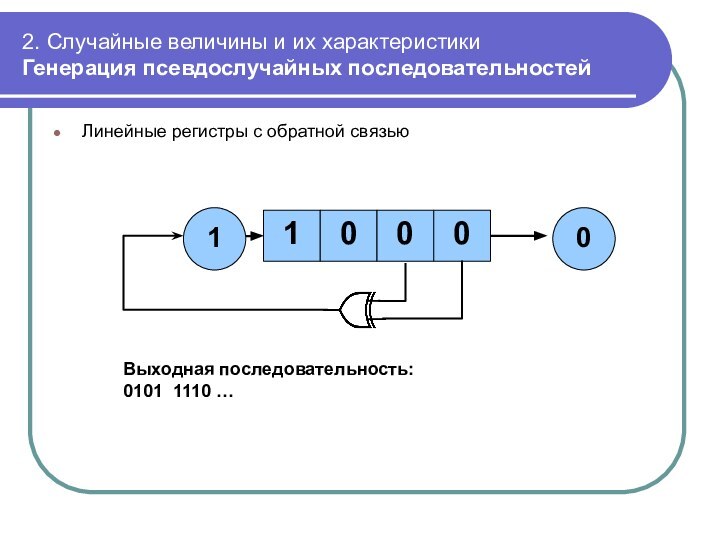
Линейные
регистры с обратной связью
1
0
0
0
0
1
Выходная последовательность:
0101 1110 …
Слайд 55
2. Случайные величины и их характеристики
Генерация псевдослучайных последовательностей
Недостатки
генераторов псевдослучайных чисел:
Конечный период
Последовательные значения не являются независимыми.
Некоторые биты
«менее случайны», чем другие.
Неравномерное одномерное распределение.
Обратимость.
Слайд 56
2. Случайные величины и их характеристики
Генерация псевдослучайных последовательностей
Основные
критерии криптостойкости:
Нет аналитической зависимости между последовательно сгенерированными числами
Зная предыдущие
числа, нельзя найти следующее (атака из прошлого)
Зная последующие числа, нельзя восстановить предшествующие (атака из будущего)
Вероятность появления любого числа в последовательности одинакова