Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему Выполнила работу: студентка группы ГТ-11,Бикназарова А.А.

Содержание

2. Определение комплексного числа Комплексные числа называются
3. Мнимая единица Мнимая единица — число, квадраткоторого
4. Пример:
5. Равные комплексные числаСравнение: x + yi =
6. Комплексная плоскостьРассмотрим координатную плоскость ипоставим в соответствие
7. Ось абсцисс –вещественная ось, а ось
9. Комплексно-сопряженные Комплексное число
11. Пример №1:Найдите число, сопряжённое ккомплексному числу (1 + 2i)(3 – 4i).Решение:Имеем Следовательно, Ответ. 11 – 2i.
12. Пример №2:Вычислите :Решение:Имеем Ответ. i.
13. Алгебраическая формаЗапись комплексного числа в виде
14. Сложение комплексных чиселСуммой двух комплексных чисел z1
15. Пример: Пусть , Тогда:
16. Вычитание комплексных чиселz = (x+yi) - (c+di)
17. Пример: Пусть
18. Произведение комплексных чиселПроизведением комплексных чисел z 1=
19. Пример: Пусть , Тогда:
20. Деление комплексных чисел Деление комплексных чиселопределяется, как домножениечислителя на выражение, сопряженноезнаменателю.Результат определен для всех
21. Пример: Пусть
22. Тригонометрическая форма Если вещественную
23. Пример Записать число
24. Произведение и частное Арифметические действия над комплексными числами,
25. Видно, что в тригонометрической форме операции
26. Первая формула Муавра В частности, если все эти
27. ПримерВычислить если Рисунок
28. Как было найдено в предыдущем примере, данное
29. Аналогичная формула применима также и при вычислении
31. Показательная форма Показательная форма записи
32. Показательная и тригонометрическиефункции в
33. Пусть комплексное число втригонометрической форме
34. Так же, как и
35. Скачать презентацию
36. Похожие презентации

Определение комплексного числа Комплексные числа называются числа вида: z = x + i y, где x и y - действительные числа.

Главная
Разное
Выполнила работу: студентка группы ГТ-11,Бикназарова А.А.

Выполнила работу: студентка группы ГТ-11, Бикназарова А.А. Множество комплексных чисел

Определение комплексного числа Комплексные числа называются числа вида: z =

Мнимая единица Мнимая единица — число, квадраткоторого равен −1. Таким образом

Равные комплексные числаСравнение: x + yi = c + di означает, что

Комплексная плоскостьРассмотрим координатную плоскость ипоставим в соответствие каждомукомплексному числу

Ось абсцисс –вещественная ось, а ось ординат-мнимая ось.С каждой точкой комплексной

Выполнила работу: студентка группы ГТ-11,Бикназарова А.А.

Комплексно-сопряженные Комплексное число

Пример №1:Найдите число, сопряжённое ккомплексному числу (1 + 2i)(3 – 4i).Решение:Имеем Следовательно, Ответ. 11 – 2i.

Пример №2:Вычислите :Решение:Имеем Ответ. i.

Алгебраическая формаЗапись комплексного числа в виде

Сложение комплексных чиселСуммой двух комплексных чисел z1 = x+ yi и z2

Вычитание комплексных чиселz = (x+yi) - (c+di) = (x-c) + (y-d)i. Разностью

Произведение комплексных чиселПроизведением комплексных чисел z 1= x + yi и z2

Деление комплексных чисел Деление комплексных чиселопределяется, как домножениечислителя на выражение, сопряженноезнаменателю.Результат определен для всех

Тригонометрическая форма Если вещественную x и мнимую y части

Произведение и частное Арифметические действия над комплексными числами, записанными в тригонометрической форме, производятся

Видно, что в тригонометрической форме операции умножения и деления производятся особенно

Первая формула Муавра В частности, если все эти числа равны между собой, то

Как было найдено в предыдущем примере, данное число в тригонометрической форме имеет

Аналогичная формула применима также и при вычислении корней -ой

Показательная форма Показательная форма записи комплексных чисел, тесно связанна с

Показательная и тригонометрическиефункции в области комплексных чиселсвязаны между собой

Пусть комплексное число втригонометрической форме имеет вид На

Так же, как и в тригонометрическойформе, здесь

Пример Пусть . Напишите показательную форму

Слайды презентации

Слайд 2 Определение комплексного числа
Комплексные числа называются числа

Определение комплексного числа Комплексные числа называются числа вида: z = x

вида:
z = x + i y,

где x и y - действительные числа.

Слайд 3 Мнимая единица
Мнимая единица — число, квадрат
которого равен

−1.
Таким образом i —это решение
уравнения

или
Степени i повторяются в цикле:
, , ,
, .

Слайд 4 Пример:

Слайд 5 Равные комплексные числа
Сравнение:

x + yi = c

Равные комплексные числаСравнение: x + yi = c + di означает,

+ di означает, что x = c и y

= d

(два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).

Слайд 6 Комплексная плоскость
Рассмотрим координатную плоскость и
поставим в соответствие каждому
комплексному

числу точку с
координатами

.
Тогда устанавливается взаимно
однозначное соответствие между полем
и множеством точек координатной
плоскости. Координатную плоскость в этом
случае будем называть комплексной
плоскостью.

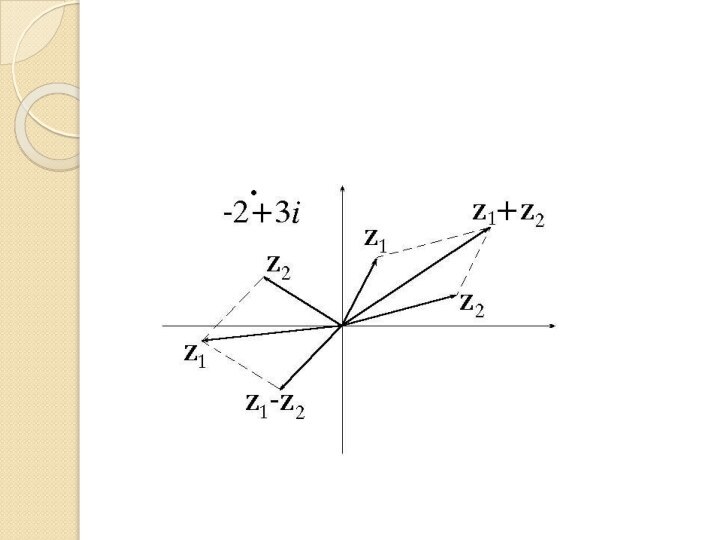
Слайд 7 Ось абсцисс –вещественная ось, а ось ординат-мнимая

Ось абсцисс –вещественная ось, а ось ординат-мнимая ось.С каждой точкой

ось.
С каждой точкой комплексной плоскости можно
связать вектор, идущий из

нуля в эту точку
(радиус-вектор). Координаты этого вектора —
вещественная и мнимая части его конца.

Радиус-вектор числа равен сумме радиус-векторов чисел и .
Аналогично с вычитанием.

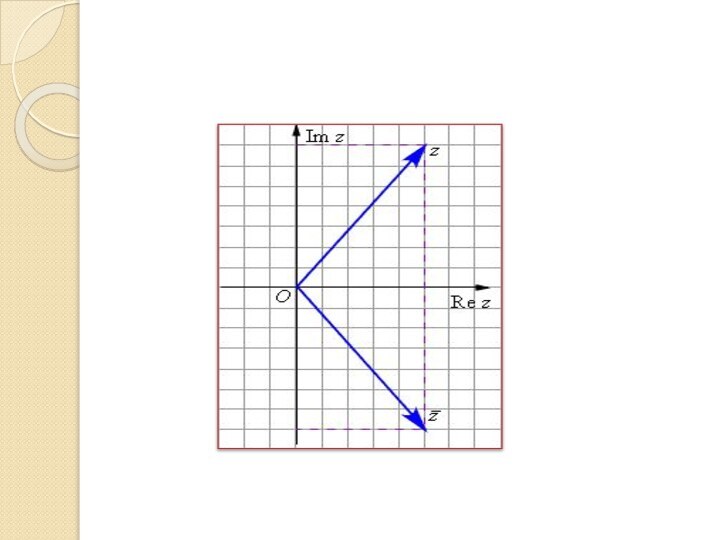
Слайд 9 Комплексно-сопряженные
Комплексное число

Комплексно-сопряженные Комплексное число z =

z =

x– iy
называется сопряженным числу
z = x+ iy.
Два комплексных числа, отличающиеся
лишь знаком комплексной
части , называются комплексно-
сопряженными .

Слайд 11 Пример №1:
Найдите число, сопряжённое к
комплексному числу (1 + 2i)(3 – 4i).
Решение:
Имеем
Следовательно,

Ответ. 11 – 2i.

Слайд 12 Пример №2:
Вычислите :

Решение:
Имеем
Ответ. i.

Слайд 13 Алгебраическая форма
Запись комплексного числа в виде

z = x+ iy
называется алгебраической формой
комплексного числа.
Число называют вещественной
(реальной) частью комплексного числа
и обозначают .
Число называют мнимой частью
комплексного числа
и обозначают .

Слайд 14 Сложение комплексных чисел
Суммой двух комплексных чисел z1 =

Сложение комплексных чиселСуммой двух комплексных чисел z1 = x+ yi и

x+ yi и z2 = c + di называется

комплексное число
z = (x+c) + (y+d)i.

Слайд 15 Пример:
Пусть

,
Тогда:

Слайд 16 Вычитание комплексных чисел
z = (x+yi) - (c+di) =

Вычитание комплексных чиселz = (x+yi) - (c+di) = (x-c) + (y-d)i.

(x-c) + (y-d)i.
Разностью двух комплексных чисел z1= a

+ bi и z2= с + di называется комплексное число х + уi, которое в сумме с вычитаемым дает уменьшаемое.

Слайд 17 Пример:
Пусть

,

Тогда:

Слайд 18 Произведение комплексных чисел
Произведением комплексных чисел
z 1= x

Произведение комплексных чиселПроизведением комплексных чисел z 1= x + yi и

+ yi и z2 = c + di
называется

комплексное число
z = (xc-yd) + (xd + yc)i,
z1z2 = (x+ yi)(c + di) = (xc - yd) + (xd + yc)i.

Слайд 19 Пример:
Пусть

,
Тогда:

Слайд 20 Деление комплексных чисел
Деление комплексных чисел
определяется, как

домножение
числителя на выражение, сопряженное
знаменателю.

Результат определен для всех

Слайд 21 Пример:
Пусть

,

Тогда:

Слайд 22 Тригонометрическая форма
Если вещественную x

Тригонометрическая форма Если вещественную x и мнимую y части комплексного

и мнимую y части комплексного числа выразить через модуль

r = | z | и аргумент
(x = rcos φ, y = rsin φ), то всякое комплексное число z, кроме нуля, можно записать в тригонометрической форме
z = r(cos φ + isin φ).

Слайд 23 Пример
Записать число

в
тригонометрической форме.
Найдём

модуль этого числа:
Аргумент данного числа находится из системы

Значит, один из аргументов числа
равен

Получаем:

Ответ.

Слайд 24 Произведение и частное
Арифметические действия над комплексными числами, записанными

Произведение и частное Арифметические действия над комплексными числами, записанными в тригонометрической форме,

в тригонометрической форме, производятся следующим образом. Пусть z1 =

r1(cos φ1 + i sin φ1) и z2 = r2(cos φ2 + i sin φ2). Имеем:

Слайд 25 Видно, что в тригонометрической форме операции умножения

Видно, что в тригонометрической форме операции умножения и деления производятся

и деления производятся особенно просто: для того, чтобы перемножить

(разделить) два комплексных числа, нужно перемножить (разделить) их модули и сложить (вычесть) их аргументы.
Отсюда следует, что для того чтобы перемножить n комплексных чисел, нужно перемножить их модули и сложить аргументы: если φ1, φ2, ..., φn – аргументы чисел z1, z2, ..., zn, то

Слайд 26 Первая формула Муавра
В частности, если все эти числа

Первая формула Муавра В частности, если все эти числа равны между собой,

равны между собой, то получим формулу, позволяющую возводить комплексное

число в любую натуральную степень.
Первая формула Муавра:

Где r — модуль, а — аргумент комплексного числа.

Слайд 27 Пример
Вычислить если
Рисунок

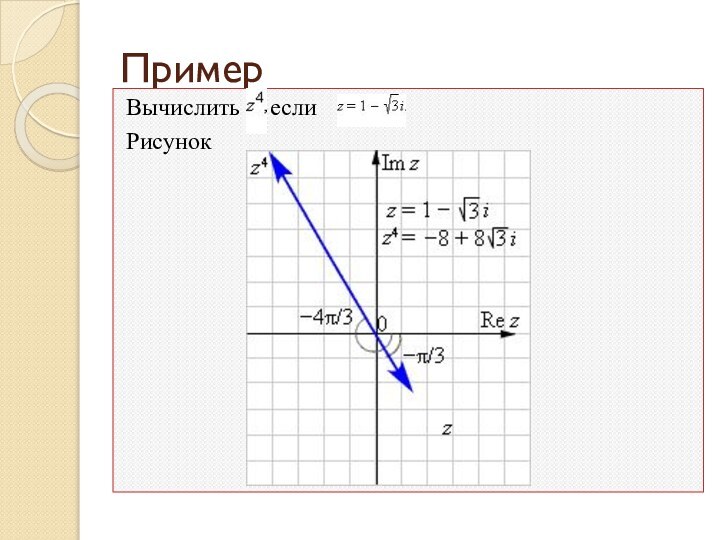
Слайд 28 Как было найдено в предыдущем примере, данное число

Как было найдено в предыдущем примере, данное число в тригонометрической форме

в тригонометрической форме имеет вид

По первой формуле Муавра получаем:

Ответ.

Слайд 29 Аналогичная формула применима также и при вычислении корней

Аналогичная формула применима также и при вычислении корней -ой степени

-ой степени из ненулевого комплексного числа:

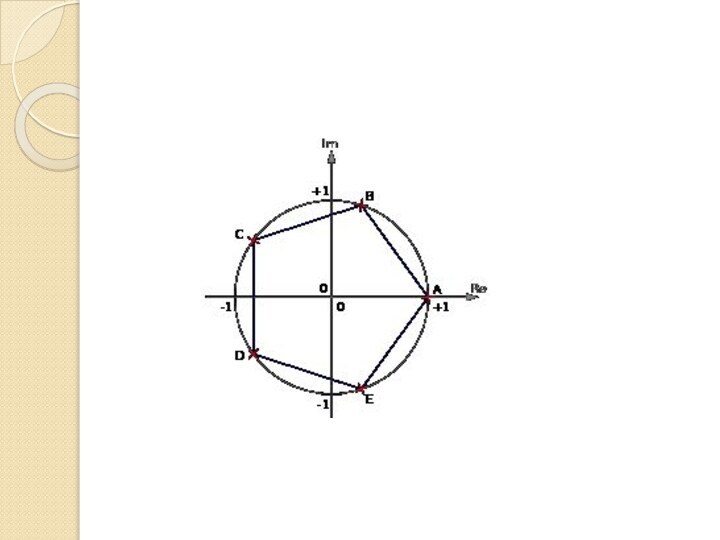
Отметим, что корни -й степени из ненулевого комплексного числа всегда существуют, и их количество равно . На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного -угольника, вписанного в окружность радиуса с центром в начале координат (см. рисунок).