нахождением:
Угла между прямыми
Угла между прямой и плоскостью
Угла между двумя плоскостями
Расстояния от точки до прямой
Расстояния от точки до плоскости
Расстояния между двумя прямыми
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


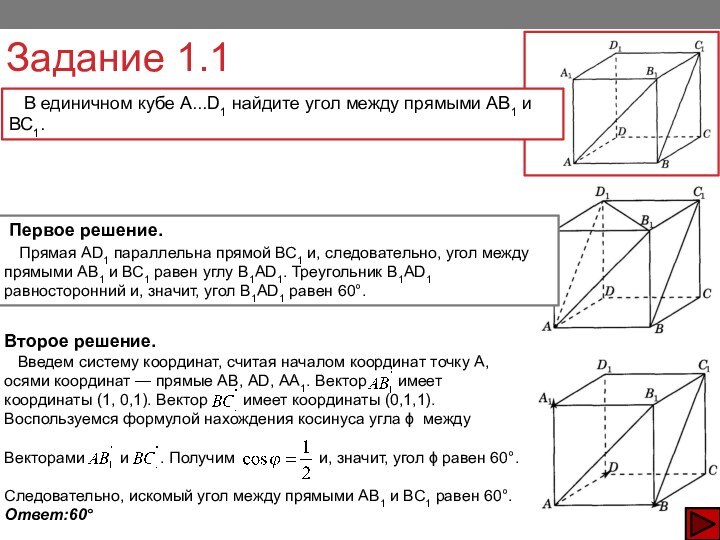


















Второе решение.
Введем систему координат, считая началом координат точку А, осями координат — прямые АВ, AD, АА1. Вектор имеет координаты (1, 0,1). Вектор имеет координаты (0,1,1). Воспользуемся формулой нахождения косинуса угла между
Векторами и . Получим и, значит, угол равен 60°.
Следовательно, искомый угол между прямыми АВ1 и ВС1 равен 60°.
Ответ:60°
Второе решение.
Введем систему координат, считая началом координат точку А, осями координат — прямые АВ, AD, АА1. Вектор имеет координаты (0, -1,1). Вектор имеет координаты (-1,1,1). Скалярное произведение этих векторов равно нулю и, значит, искомый угол между прямыми DA1 и BD1, равен 90°.
Ответ: 90°
Первое решение.
Обозначим D и F1 соответственно середины ребер АС и А1В1.Прямые DC1 и DF1 будут соответственно параллельны AD1 и CE1. Следовательно, угол между прямыми AD1 и CE1 будет равен углу C1DF1.
Треугольник C1DF1 равнобедренный, , .
Используя теорему косинусов, получаем
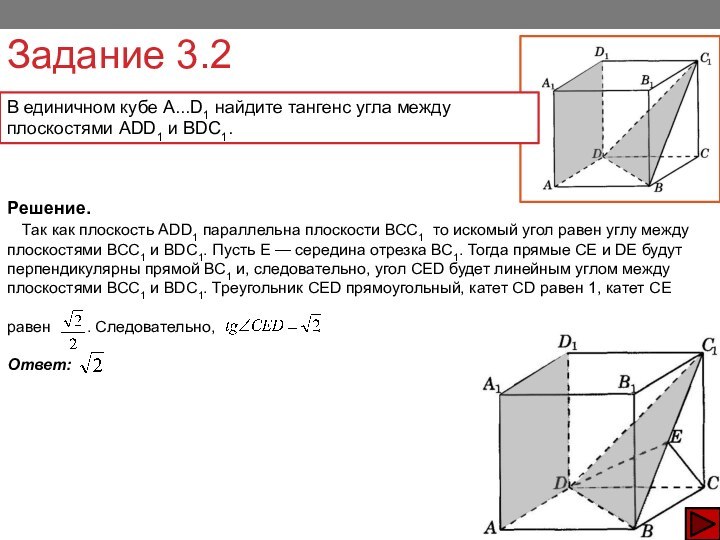
Решение.
Пусть О — центр нижнего основания призмы. Прямая ВО параллельна AF. Так как плоскости ABC и ВСС1 перпендикулярны, то искомым углом будет угол ОВС. Так как треугольник ОВС равносторонний, то этот угол будет равен 60°.
Ответ: 60°
Решение.
Так как прямые ВВ1 и СС1 параллельны, то искомый угол будет равен углу между прямой ВВ1 и плоскостью BDE1. Прямая BD, через которую проходит плоскость BDE1, перпендикулярна плоскости АВВ1 и, значит, плоскость BDE1 перпендикулярна плоскости АВВ1. Следовательно, искомый угол будет равен углу А1ВВ1; т. е. равен 45°.
Ответ: 45°
Решение.
Через вершину S проведем прямую, параллельную прямой АВ, и отложим на ней отрезок SF, равный отрезку АВ. В тетраэдре SBCF все ребра равны 1 и плоскость BCF параллельна плоскости SAD. Перпендикуляр ЕH, опущенный из точки Е на плоскость BCF,
равен половине высоты тетраэдра, т. e равен . Угол между прямой BE и плоскостью SAD
равен углу ЕВН, синус которого равен .
Ответ:
Первое решение.
Так как плоскость FCC1 параллельна плоскости DEE1, то искомый угол равен углу между плоскостями AFF1 и FCC1. Так как плоскости AFF1 и FCQ перпендикулярны плоскости ABC, то соответствующим линейным углом будет угол AFC, который равен 60°.
Второе решение.
Так как плоскость AFF1 параллельна плоскости BEE1, то искомый угол равен углу между плоскостями ВЕЕ1 и DEE1. Так как плоскости ВЕЕ1 и DEE1 перпендикулярны плоскости ABC, то соответствующим линейным углом будет угол BED, который равен 60°
Ответ: 60°
Решение:
Пусть DE—линия пересечения данных плоскостей, F — середина отрезка DE, G — середина отрезка А1С1. Угол GFB1 является линейным углом между данными плоскостями.
В треугольнике GFB1 имеем: По теореме косинусов
находим
Ответ:
Решение.
Так как прямая D1F1 перпендикулярна плоскости AFF1, то отрезок AF1 будет искомым перпендикуляром, опущенным из точки А на прямую D1F1. Его длина равна
Ответ:
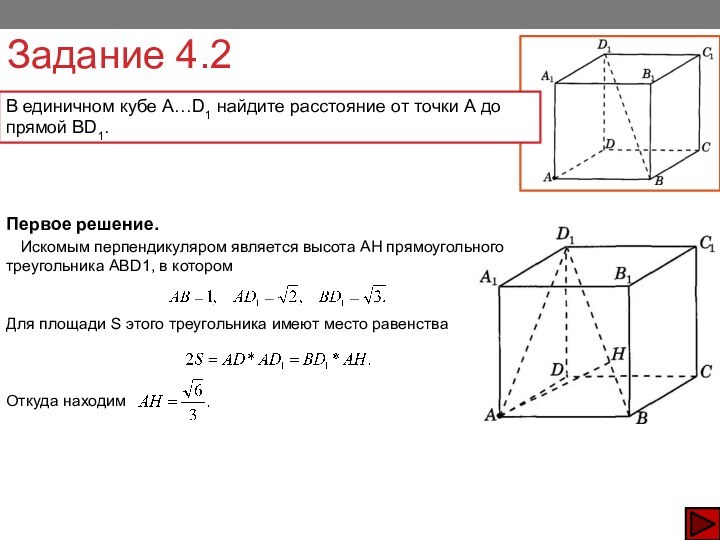
Третье решение.
Искомым перпендикуляром является высота АН прямоугольного треугольника ABD1; в котором
Откуда и, следовательно,
Ответ:
Решение:
Искомое расстояние от точки F до прямой BG равно высоте FH треугольника FBG, в
котором По теореме Пифагора находим
Ответ:
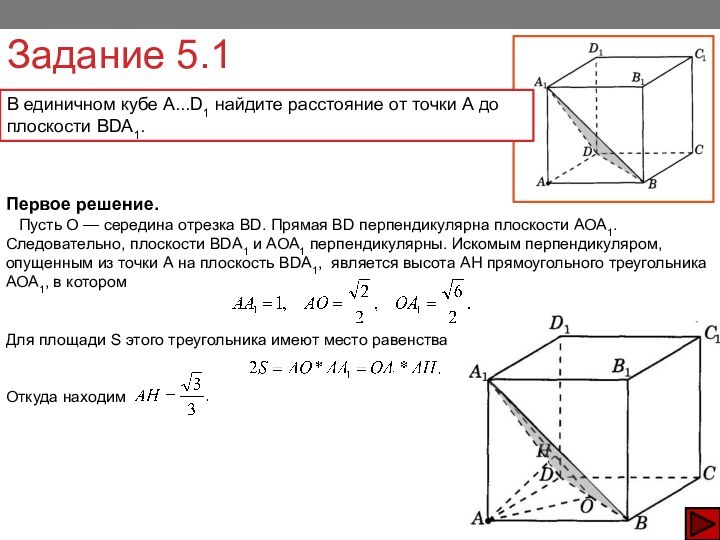
Третье решение.
Пусть О — середина отрезка BD. Прямая BD перпендикулярна плоскости АОА1. Следовательно, плоскости BDA1 и АОА1 перпендикулярны. Искомым перпендикуляром, опущенным из точки А на плоскость BDA1, является высота АН прямоугольного треугольника АОА1 в котором
Откуда и, следовательно,
Ответ:
В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите расстояние от точки А до плоскости SBC.
Первое решение.
Пусть О и О1 — центры оснований призмы. Прямая АО1 параллельна плоскости BFE1 и, следовательно, расстояние от точки А до плоскости BFE1 равно расстоянию от прямой АО1 до плоскости BFE1 . Плоскость AOO1 перпендикулярна плоскости BFE1 и, следовательно, расстояние от прямой А01 до плоскости BFE1 равно расстоянию от прямой AO1 до линии пересечения GG1 плоскостей АОО1 и BFE1. Треугольник А001 прямоугольный, АО = ОО1 = 1, GG1 — его средняя линия. Следовательно, расстояние между прямыми АО1 и GG1 равно
половине высоты ОН треугольника АОО1 т. е. равно
Решение.
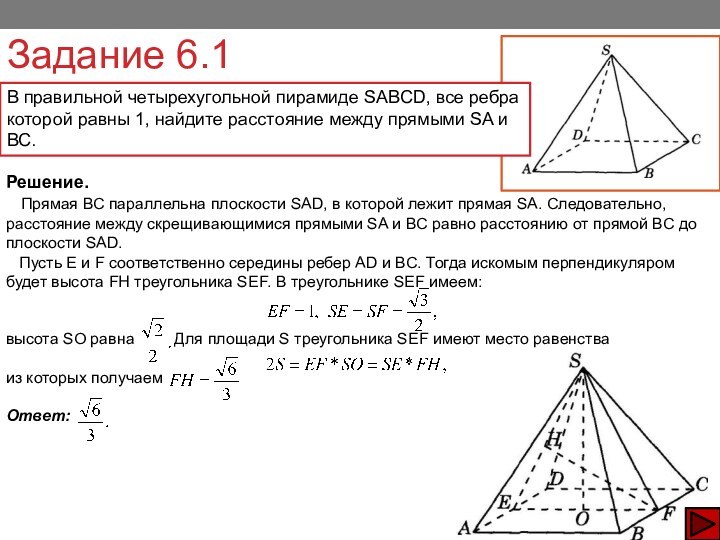
Прямая ВС параллельна плоскости SAD, в которой лежит прямая SA. Следовательно, расстояние между скрещивающимися прямыми SA и ВС равно расстоянию от прямой ВС до плоскости SAD.
Пусть Е и F соответственно середины ребер AD и ВС. Тогда искомым перпендикуляром будет высота FH треугольника SEF. В треугольнике SEF имеем:
высота SO равна Для площади S треугольника SEF имеют место равенства
из которых получаем
Ответ:
Задание 6.3
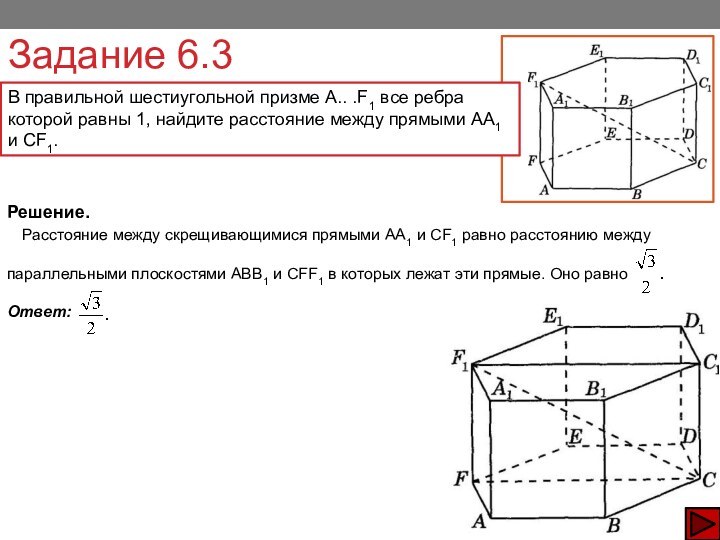
Решение.
Расстояние между скрещивающимися прямыми АA1 и CF1 равно расстоянию между
параллельными плоскостями АВВ1 и СFF1 в которых лежат эти прямые. Оно равно
Ответ: