- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Урок алгебры в 9 классе. Построение графика квадратичной ункции
Содержание
- 2. Построение графика квадратичной функции
- 3. Функция (от латинского) – исполнение,
- 4. Знать: алгоритм построения графика квадратичной функции;
- 5. Вариант №11.Не строя график функции y=x²+4x+3, найти
- 6. Вариант № 2.1. Найдите координаты точки
- 7. Ответы: вариант 11. Г2. А3. Б вариант 21. Б2. Г3. А
- 8. Преобразование графика квадратичной функции.
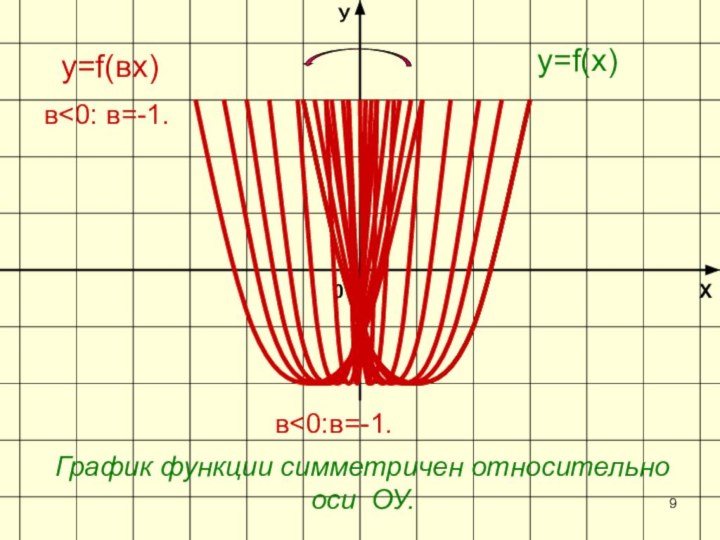
- 9. ХУ0y=f(вх)y=f(х)в
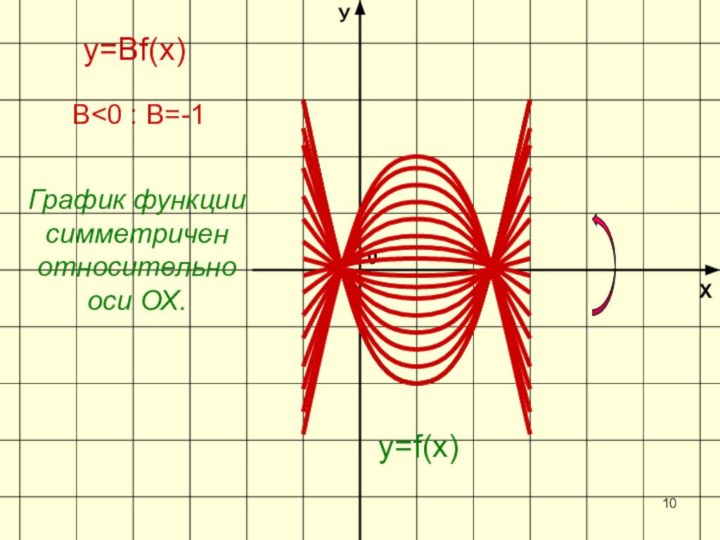
- 10. ХУ0y=f(х)y=Вf(х)В
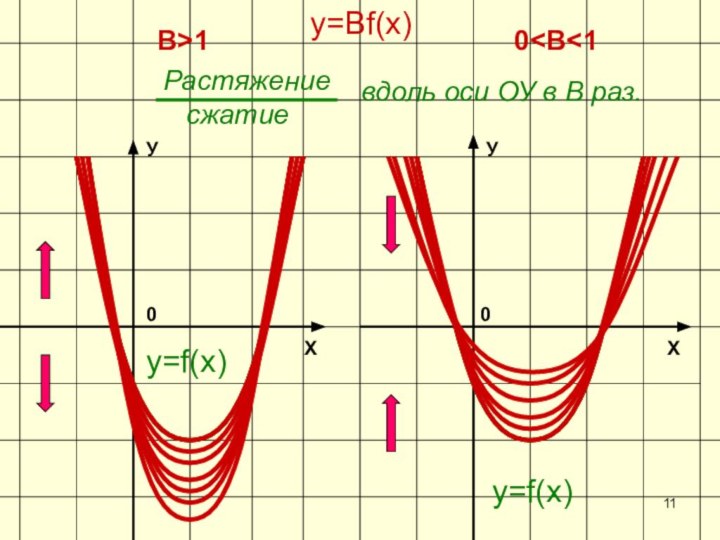
- 11. ХУ0y=f(х)ХУ0y=f(х)y=Вf(х)В>10
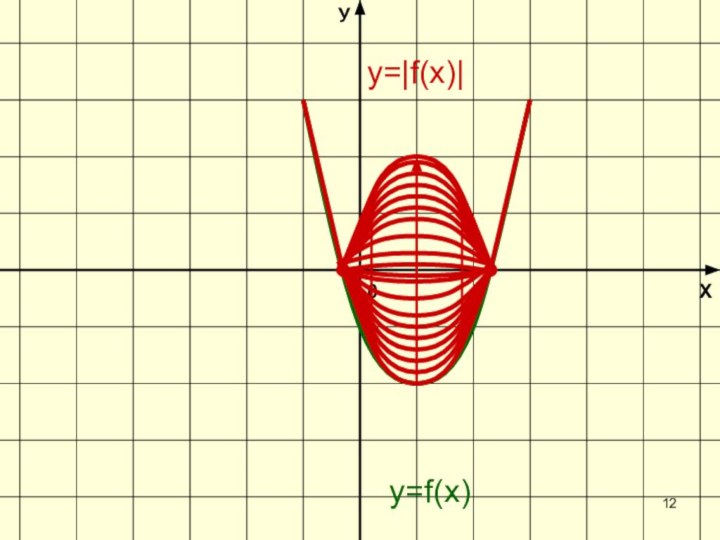
- 12. ХУ0y=f(х)y=|f(х)|
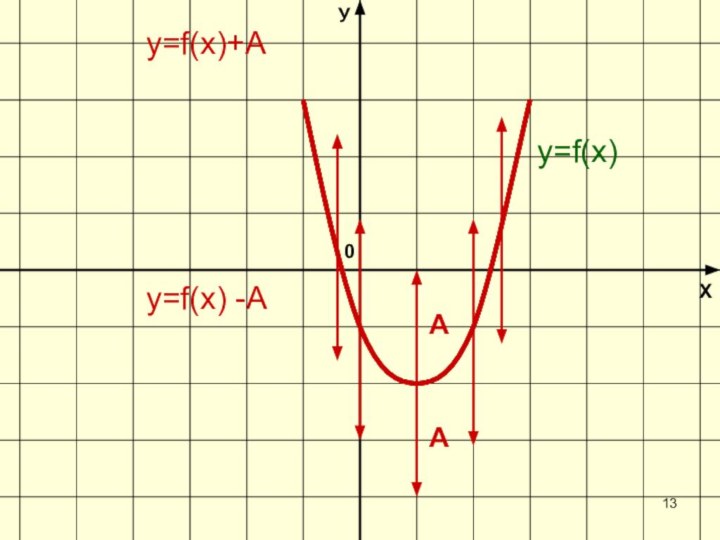
- 13. ХУ0y=f(х) -Аy=f(х)+Аy=f(х)
- 14. Можно показать ,что любую квадратичную
- 15. Функция у=ах2+вх+с
- 16. Рассмотрим несколько примеров:Y=x2Y=(x- 1)2Y=(x+2)2Y=(x-1)2+3Y=(x+2)2-
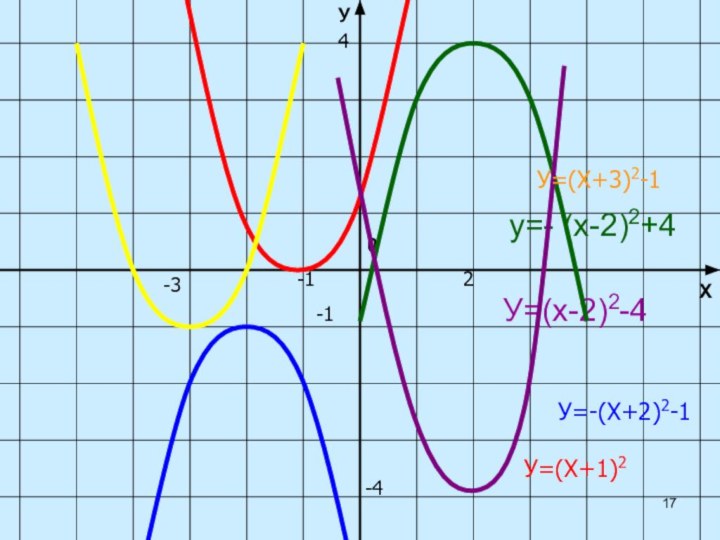
- 17. ХУ0У=(х-2)2-4y=- (х-2)2+4-12-44-3-1У=(Х+3)2-1У=-(Х+2)2-1У=(Х+1)2
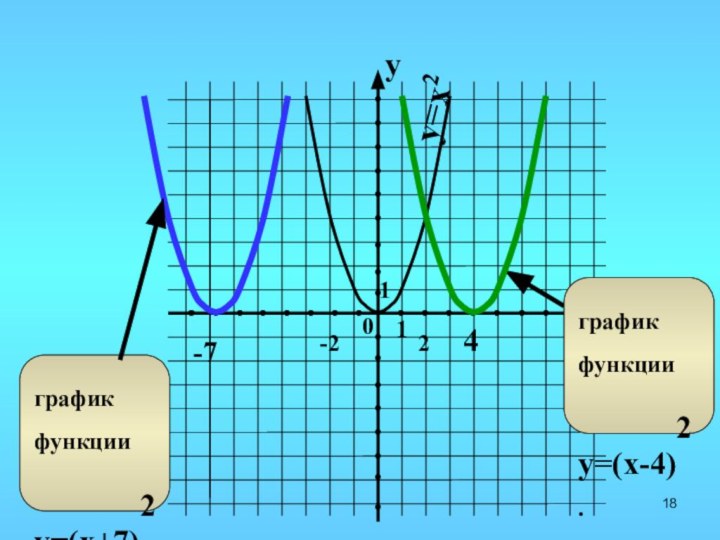
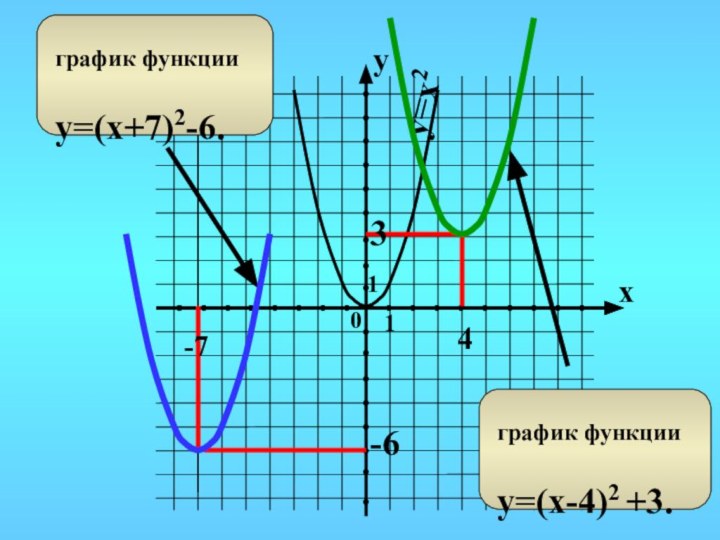
- 18. y=x24-7
- 19. y=x24-63-7
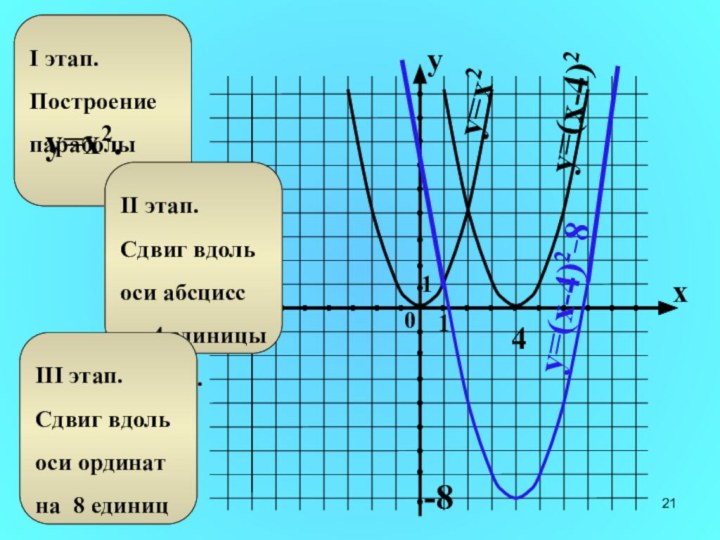
- 21. y=x24-8y=(x-4)2
- 22. Функция и живопись, что между ними общего? The Code of Da Vinchi
- 23. Построение графика квадратичной функцииЗадача. Построить график функции
- 24. Рассмотрим построение графика в случае отрицательного дискриминанта.Задача.
- 25. Схема построения графика квадратичной функции y=ax2+bx+c:1. Построить
- 26. Скачать презентацию
- 27. Похожие презентации

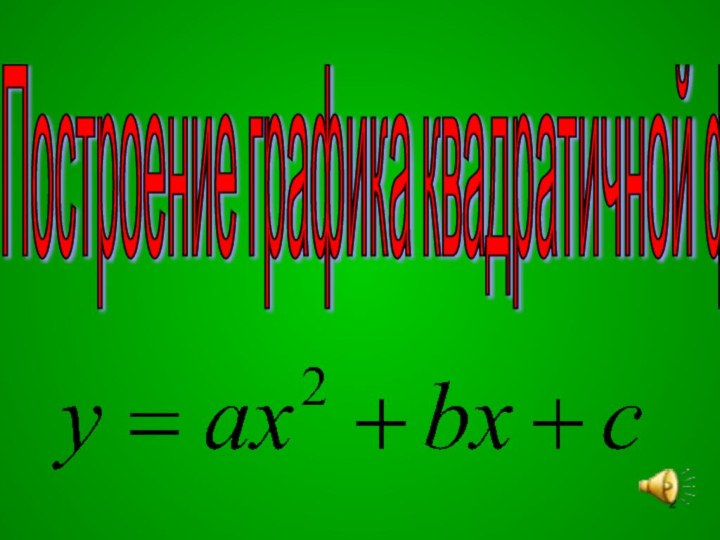











Слайд 4
Знать: алгоритм построения графика квадратичной функции;
Уметь: строить
график любой квадратичной функции, определять основные свойства функции по
графику.
Слайд 5
Вариант №1
1.Не строя график функции y=x²+4x+3, найти y
при x=1.
А. 2; Б.-4;
В. 3; Г. 8.2. Принадлежит ли точка М (1;-6) параболе y=-3x²+4x-7?
А. Да; Б.Нет; В. Не знаю.
3. По рисунку определите промежутки убывания функции.
4
-3
А. y<4; Б. x≥ -3; В. x<-3; Г. y≥4.
Тестовое задание.
Слайд 6
Вариант № 2.
1. Найдите координаты точки пересечения графика
функции y=x²-3x+5 с осью Оy.
А. (5; -4);
Б. (0; 5); В.(5; 0); Г. Другой ответ. 2. По рисунку определите при каких значениях x функция y=ax²+bx+c принимает положительные значения?
А. -2 ≤ x ≤ 6; Б. x> -2; В. x ≤ 6; Г. x < -2 и x > 6.
3. Записать уравнение параболы, полученной сдвигом параболыy=2x² вдоль оси Ox 1,5 единиц вправо и последующим сдвигом вдоль оси Oy на 3,5 единиц вверх.
А.y=2(x-1,5)²+3,5; Б.y=2(x+1,5)²+3,5; В.y=2(x-1,5)²-3,5;
Г.y=2(x+1,5)²-3,5.
Тестовое задание.
2
6
Слайд 14
Можно показать ,что любую квадратичную
функцию
у =ax2+вх +с с помощью выделения полного квадрата
можнозаписать в виде у=a(x-x0)2 +y0 , где х0= - b/(2a) ,
y0= y(x0)= - (b2-4ac)/(4a)
Графиком функции у=a(x-x0)2 +y0 является парабола,
получаемая сдвигом параболы Y=ax2 :
вдоль оси абсцисс вправо на x0,если x0 > 0,влево на |x0⏐,если х0 <0.
вдоль оси ординат вверх на y0 ,если y0> 0, вниз на⏐y0 ⏐,если
y0 < 0.
Слайд 15
Функция у=ах2+вх+с
принимает наименьшее или наибольшее значение в точке х0= -
в /2а, которая является абсциссой вершины параболы.Значение функции в точке х0 можно найти по формуле у0=у(х0).
Если а>0, то функция имеет наименьшее значение, а если
а<0, то функция имеет наибольшее значение.
Слайд 16
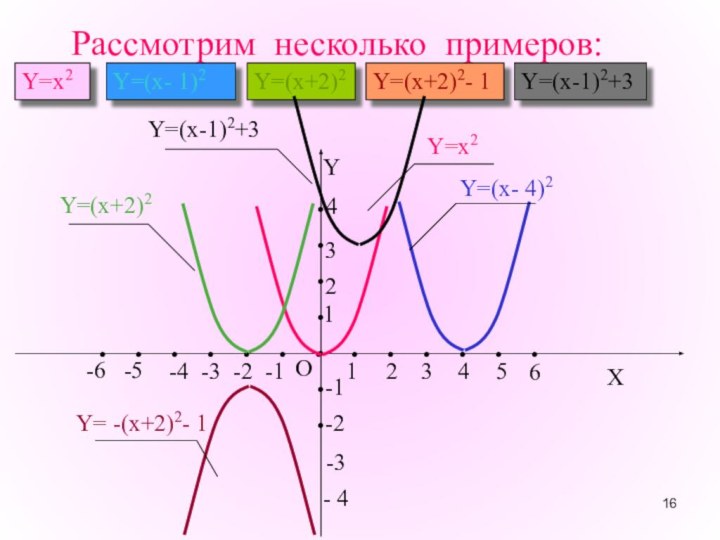
Рассмотрим несколько примеров:
Y=x2
Y=(x- 1)2
Y=(x+2)2
Y=(x-1)2+3
Y=(x+2)2- 1
.
. . . . . . . . .
. . .. . . . . . .
Y=x2
Y=(x- 4)2
Y=(x+2)2
Y= -(x+2)2- 1
Y=(x-1)2+3
Слайд 23
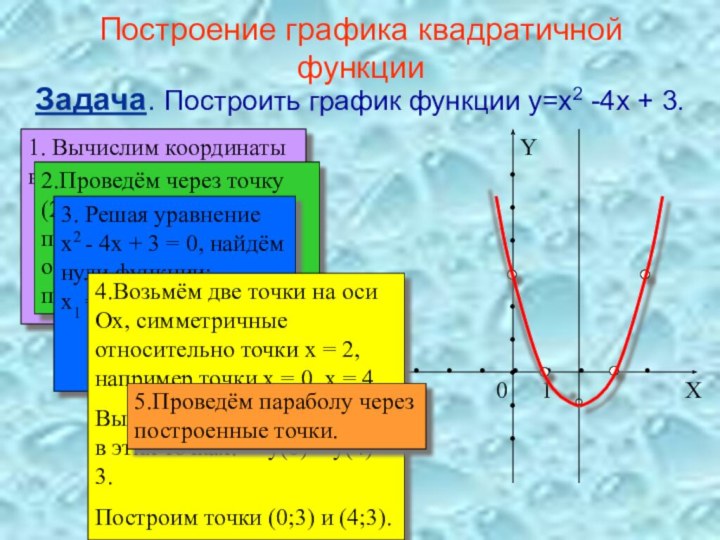
Построение графика квадратичной функции
Задача. Построить график функции y=x2
-4x + 3.
1. Вычислим координаты вершины параболы:
x0 = -
(- 4/2)=2y0 = 22 - 4*2 + 3 = -1.
Построим точку (2;-1)
1
2.Проведём через точку (2;-1) прямую, параллельную оси ординат - ось симметрии параболы.
3. Решая уравнение x2 - 4x + 3 = 0, найдём нули функции: x1 = 1, x2 = 3.
Построим точки (1;0) и (3;0).
4.Возьмём две точки на оси Оx, симметричные относительно точки x = 2, например точки x = 0, x = 4.
Вычислим значение функции в этих точках: y(0) = y(4) = 3.
Построим точки (0;3) и (4;3).
5.Проведём параболу через построенные точки.
Слайд 24
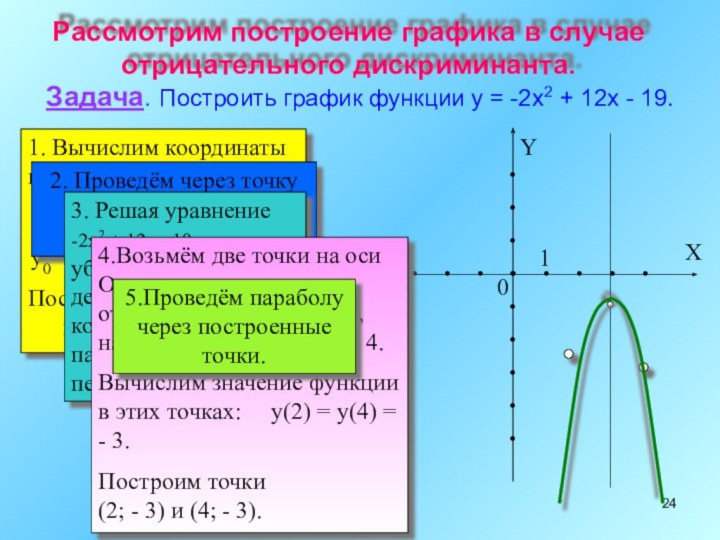
Рассмотрим построение графика в случае отрицательного дискриминанта.
Задача. Построить
график функции y = -2x2 + 12x - 19.
1.
Вычислим координаты вершины параболы:x0 = - (12/(-4)) =3
y0 = - 2*32 + 12*3 -19 = -1.
Построим точку (3;-1) - вершину параболы.
2. Проведём через точку (3;-1) ось симметрии параболы.
3. Решая уравнение -2x2 + 12x - 19, убеждаемся, что действительных корней нет, и поэтому парабола не пересекает ось Оx.
4.Возьмём две точки на оси Оx, симметричные относительно точки x = 3, например точки x = 2, x = 4.
Вычислим значение функции в этих точках: y(2) = y(4) = - 3.
Построим точки (2; - 3) и (4; - 3).
5.Проведём параболу через построенные точки.
Слайд 25
Схема построения графика
квадратичной функции y=ax2+bx+c:
1. Построить вершину параболы
(х0,у0), вычислив х0 ,у0 по
формулам х0= - (b/(2*a))
y0= y(x0). 2. Провести ось симметрии параболы.
3. Найти нули функции , если они есть и построить на оси абсцисс соответствующие точки параболы .
4. Построить две какие - нибудь точки параболы, симметричные относительно ее оси. (Например точки с абсциссам х = 0 и х = х0 ). Для точности построения можно найти еще несколько точек параболы.
5. Провести через построенные точки параболу.
.





























