Презентация на тему по подготовке к ОГЭ и ЕГЭ Решение уравнений и систем уравнений с параметрами в среде Geogebra

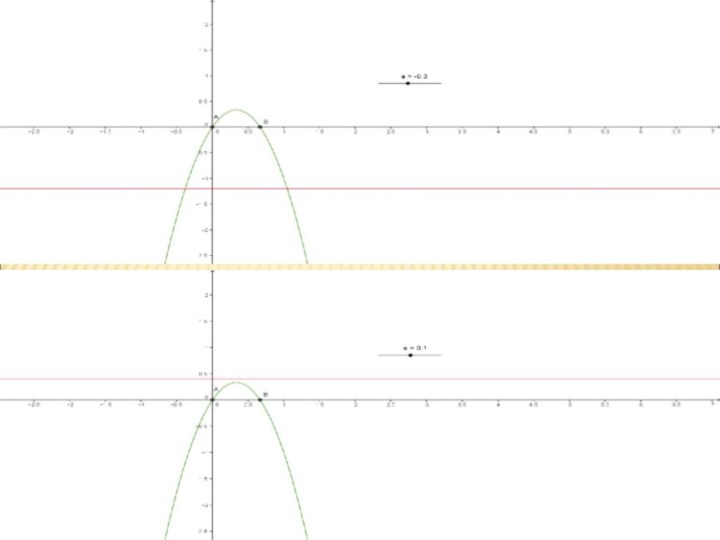
и систем уравнений с параметрами очень удобен и нагляден

графический метод решения, особенно с использованием среды GeoGebra.
На уроках математики при изучении уравнений с параметрами использование динамической математики развивает зрительное и пространственное мышление учеников.
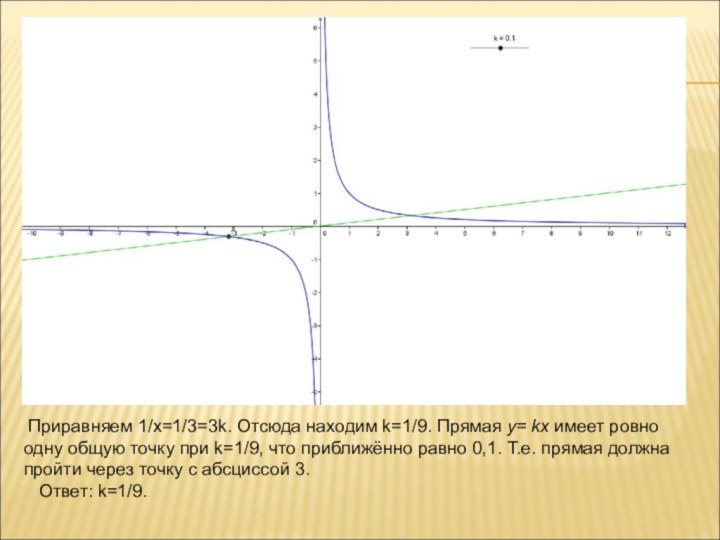
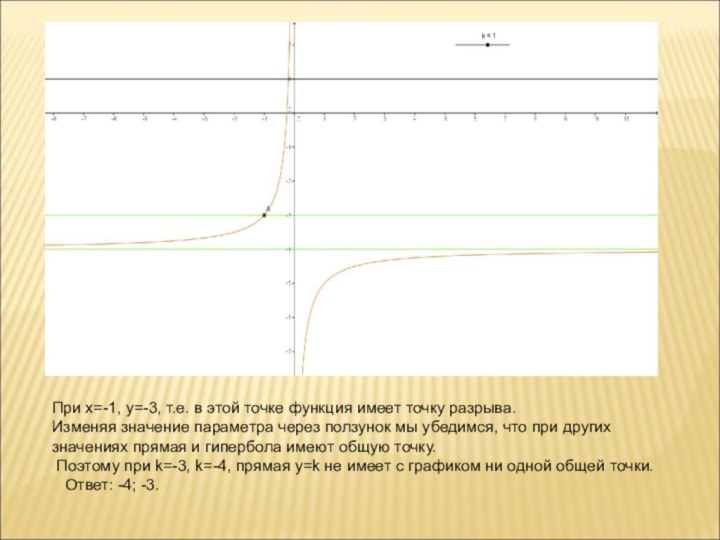
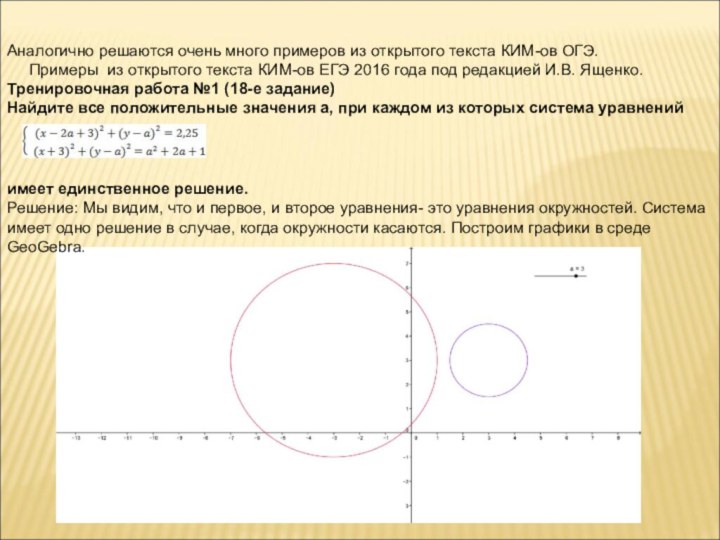
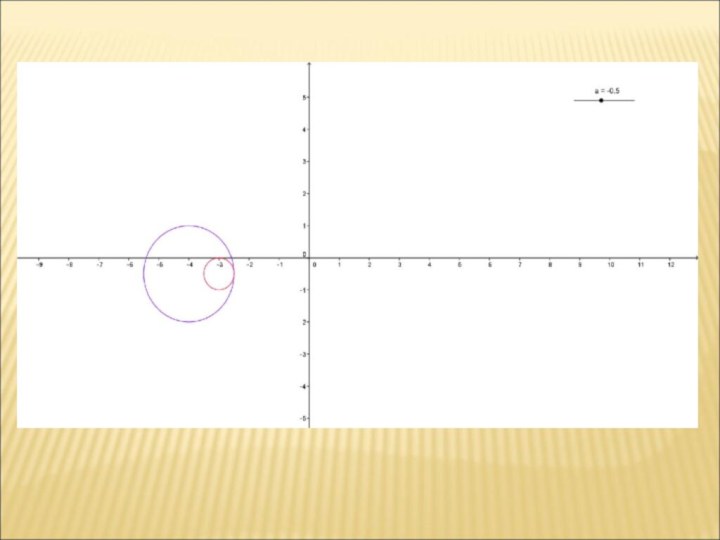
А для подготовки учащихся к ОГЭ (23-е задание части 2) и ЕГЭ (18-е задание части 2) можно использовать графический метод решения.
Рассмотрим примеры из открытого текста КИМ-ов ОГЭ 2016 года под редакцией И.В. Ященко.

и определите, при каких значениях k прямая y= kx

имеет с графиком ровно одну общую точку.
Решение: Преобразуем выражение при условии, что x≠3. Построим график:

kx имеет ровно одну общую точку при k=1/9, что

приближённо равно 0,1. Т.е. прямая должна пройти через точку c абсциссой 3.
Ответ: k=1/9.

функции
и определите, при каких значениях k

прямая y=k не имеет с графиком общих точек.
Решение: Преобразуем выражение
, при условии, что x≠-1.
Построим график:

имеет точку разрыва.
Изменяя значение параметра через ползунок мы убедимся,

что при других значениях прямая и гипербола имеют общую точку.
Поэтому при k=-3, k=-4, прямая y=k не имеет с графиком ни одной общей точки.
Ответ: -4; -3.

определите, при каких значениях k прямая y=kx имеет с

графиком ровно одну общую точку.
Решение: Преобразуем выражение

при условии, что х≠ -2. Построим график:

она проходит через точку (-2;-5) или если уравнение
имеет

один корень. Дискриминант уравнения

равен

. Получаем, что k=-2, k=2. Подставив вместо х=-2, получим k=2.5.
Ответ: 2,5; -2; 2.

КИМ-ов ОГЭ.
Примеры из открытого текста КИМ-ов

ЕГЭ 2016 года под редакцией И.В. Ященко.
Тренировочная работа №1 (18-е задание)
Найдите все положительные значения a, при каждом из которых система уравнений

имеет единственное решение.
Решение: Мы видим, что и первое, и второе уравнения- это уравнения окружностей. Система имеет одно решение в случае, когда окружности касаются. Построим графики в среде GeoGebra.

значениях параметра окружности либо пересекаются, либо не пересекаются, либо

касаются. К условию нашей задачи соответствует только одно решение: а=2,5.
Ответ: а=2,5.
ТР №7. Найдите все значения а, при каждом из которых уравнение

не имеет корней.
Решение: Преобразовав уравнение, получим, что

Найдём дискриминант квадратного уравнения и он должен быть меньше нуля: 4-48а<0, а>1/12
Построим параболу и прямую через строку ввода. Изменяя ползунок а, увидим решение. При а>1/12, они не пересекаются, т.е. данное уравнение не имеет корней. Ответ: а>1/12

из которых уравнение
не имеет корней.
Решение: Преобразовав уравнение,

получим, что

Графически:
Построим параболу и прямую через строку ввода. Изменяя ползунок а, увидим решение.
Аналитически:
Найдём дискриминант квадратного уравнения и он должен быть меньше нуля: 9+40а<0, а<-9/40.
При а<-9/40 данное уравнение не имеет корней.
Ответ: а<-9/40.

ЕГЭ- 2016.