ставится в соответствие единственный элемент из множества У, то
говорят, что на множестве Х задана функция у=f(x).
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть
















1. Она определена на симметричном относительно нуля промежутке
2. Выполняется условие
f(-x)=-f(x)
График нечетной функции проходит симметрично относительно начала координат.
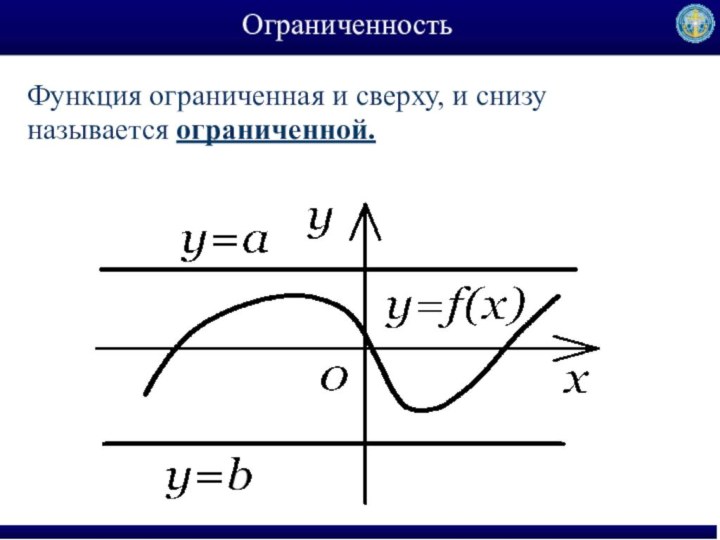
Функцию y=f(x)y=f(x) называют ограниченной сверху на множестве Х⊂D(f), если существует такое число а, что для любых хϵХ выполняется неравенство f(x) < a.