- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре на тему: Тригонометрические функции
Содержание
- 2. 1. Вычислите2. Сопоставьте графики функций и формулы их задающие.
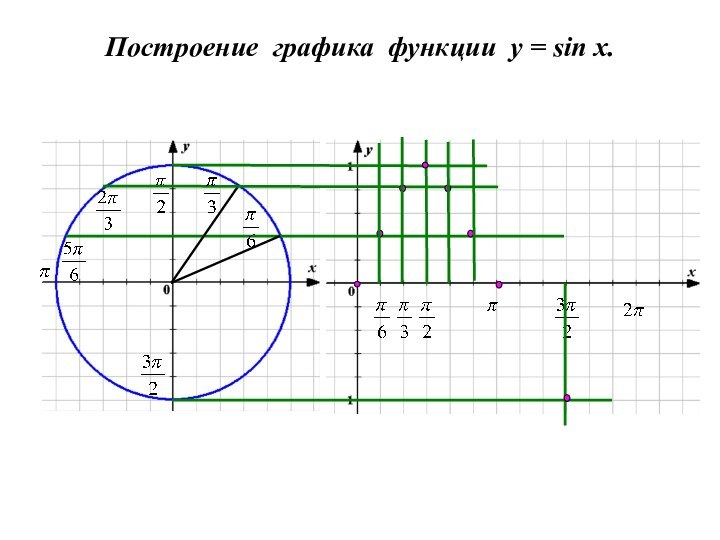
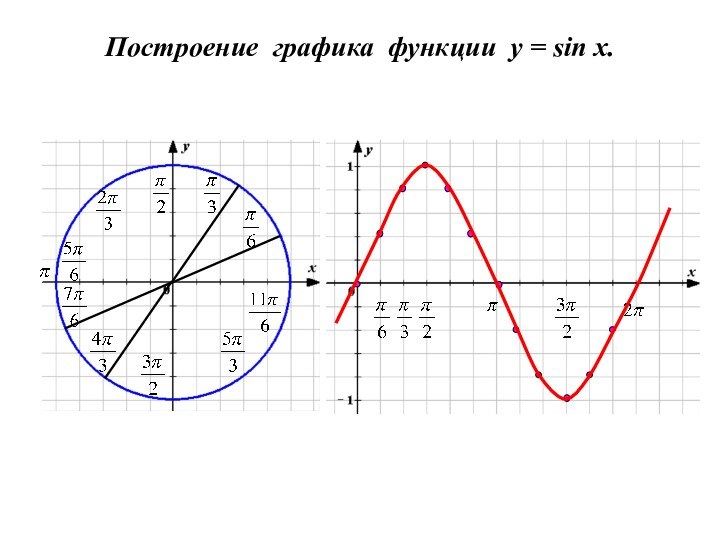
- 3. Построение графика функции y = sin x.
- 4. Построение графика функции y = sin x.
- 5. Построение графика функции y = sin x.
- 6. Функция у = sin x.3. Функция у
- 7. Функция y=sin x, график и свойства.1)D(y)= 2)E(y)=
- 8. Синусоида
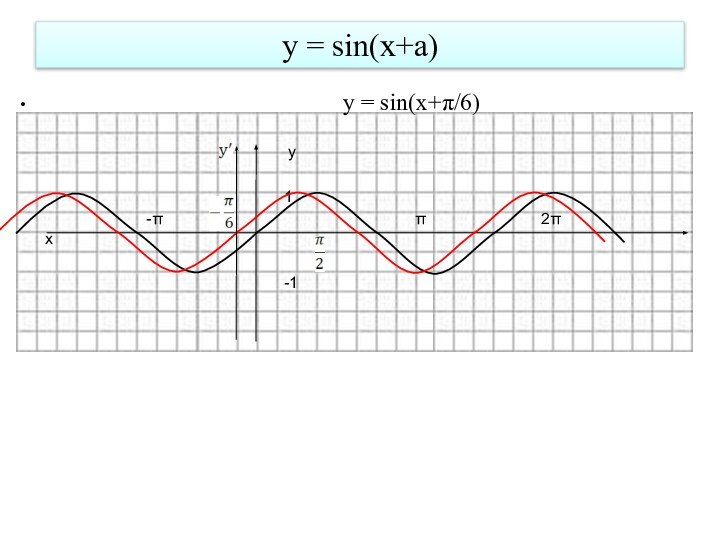
- 9. у = sin(x+a)
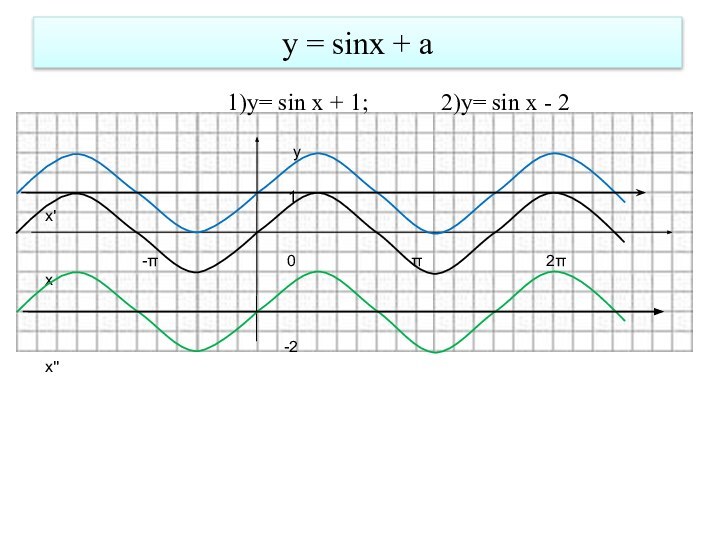
- 10. у = sinx + a
- 11. Построение графиков y=sin(x+m)+n1)y= sin x ;
- 12. Построение графика функции y = cos x.График
- 13. Функция у = соs x.3. Функция у
- 14. Функция y = cos x, её свойства
- 15. y= cos x
- 16. Построение графиков y = cos(x+m)+n
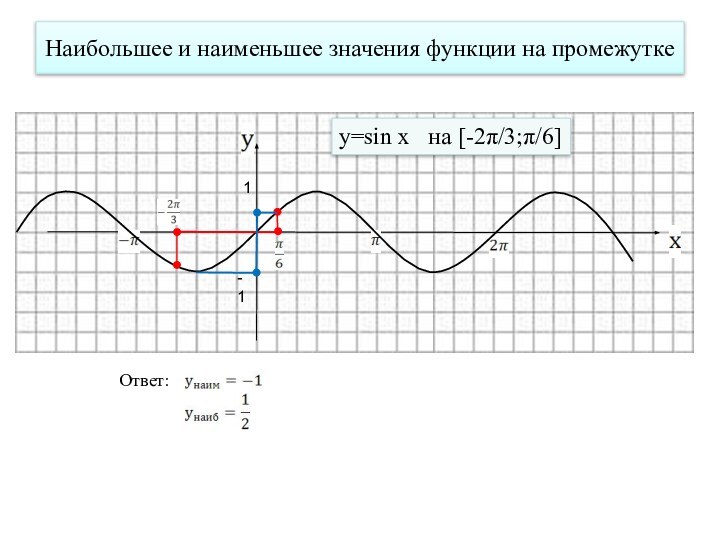
- 17. Наибольшее и наименьшее значения функции на промежутке
- 18. Скачать презентацию
- 19. Похожие презентации









![Презентация по алгебре на тему: Тригонометрические функции -ππ1-1ух-3π/23π/2y = cos x на (π/3;2π/3]Ответ:](/img/tmb/6/515262/5f03bf75a8e9ada28b2f540409ef8597-720x.jpg)
Слайд 6
Функция у = sin x.
3. Функция у =
sin α нечетная, т.к. sin (- α) = -
sin α1. Областью определения функции является множество
всех действительных чисел ( R )
2. Областью изменений (Областью значений) - [ - 1; 1 ].
Функция периодическая, с главным периодом 2π.
sin ( α + 2π ) = sin α.
5. Функция непрерывная
6. Возрастает: [ - π/2; π/2 ].
Убывает: [ π/2; 3π/2 ].
+
+
+
-
-
-
Слайд 7
Функция y=sin x, график и свойства.
1)D(y)=
2)E(y)=
3)
4)sin(-x)=-sin x
5)Возрастает
наУбывает на
6)Периодичная
Слайд 11
Построение графиков y=sin(x+m)+n
1)y= sin x ; 2)y=
sin(x+π/6); 3)y= sin(x-π/3); 4)y= sinx+1;
5)y= sinx-3/2y
1
-π 0 π 2π 3π x
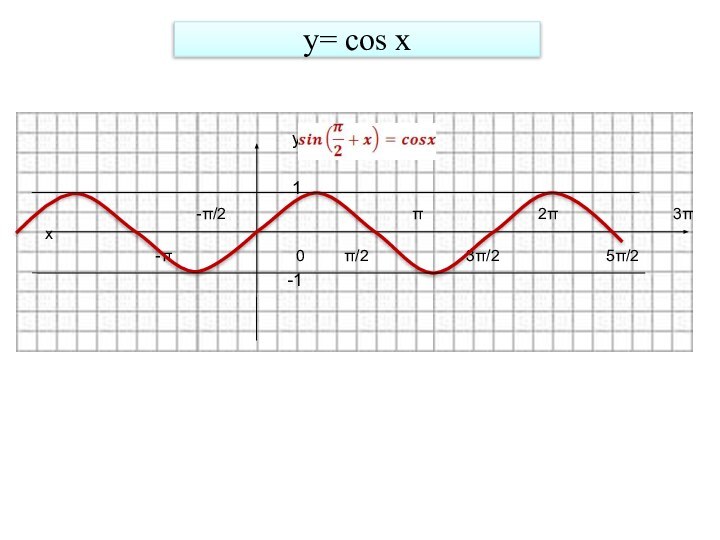
Слайд 12
Построение графика функции y = cos x.
График функции
у = cos x получается переносом
графика функции у =
sin x влево на π/2.Sin (x + π/2) = sin x cos π/2 + sin π/2 cos x = cos x
Слайд 13
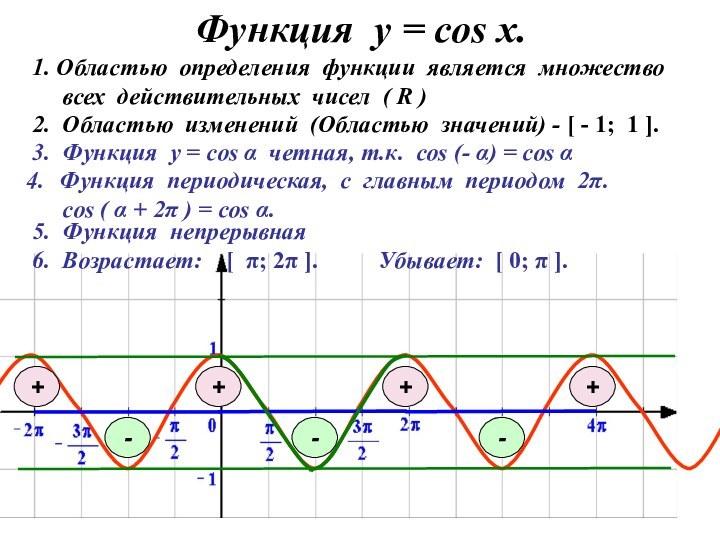
Функция у = соs x.
3. Функция у =
cos α четная, т.к. cos (- α) = cos
α1. Областью определения функции является множество
всех действительных чисел ( R )
2. Областью изменений (Областью значений) - [ - 1; 1 ].
Функция периодическая, с главным периодом 2π.
cos ( α + 2π ) = cos α.
5. Функция непрерывная
6. Возрастает: [ π; 2π ].
Убывает: [ 0; π ].
-
-
-
+
+
+
+
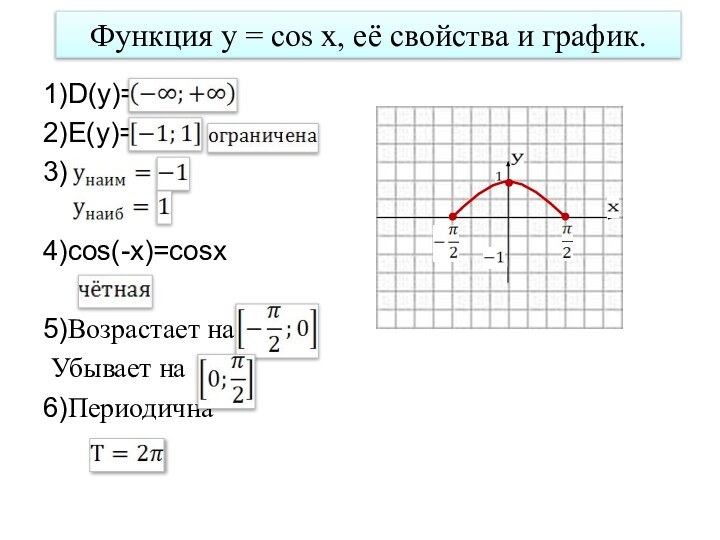
Слайд 14 Функция y = cos x, её свойства и
график.
1)D(y)=
2)E(y)=
3)
4)cos(-x)=cosx
5)Возрастает на
Убывает на
6)Периодична





























