арксинус и арккосинус числа.
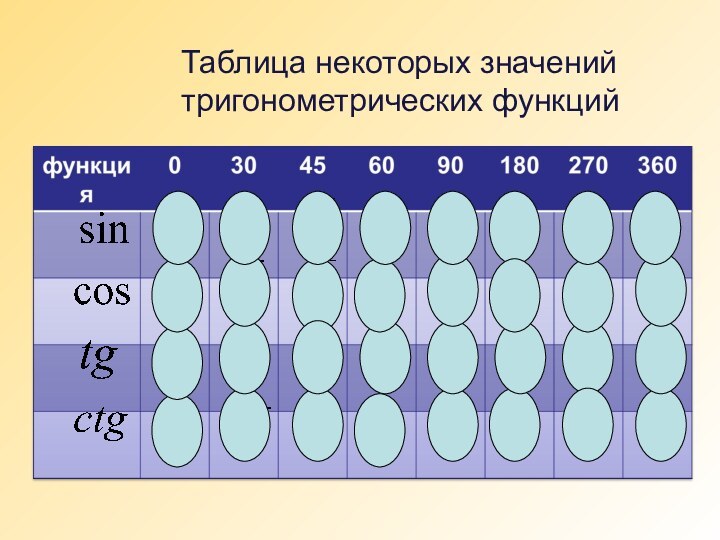
Научить вычислять их значения по таблице.
Развивать
мышление, память, вычислительные навыки, навыки самоконтроля и взаимоконтроля.Воспитывать ответственность, самостоятельность, трудолюбие.
Совершенствовать навыки устного счета





















![Презентация по алгебре и начало анализа на тему Арксинус и арккосинус(10 класс) Свойства функции y = arcsin x 1)Область определения: отрезок [-1; 1]; 2)Область](/img/tmb/6/552060/9b9c3e2f000e569e323cb6ff481e0d6a-720x.jpg)


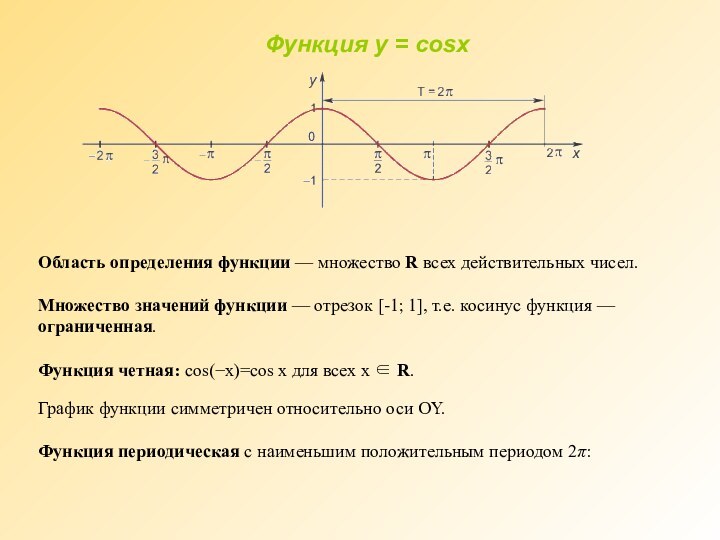
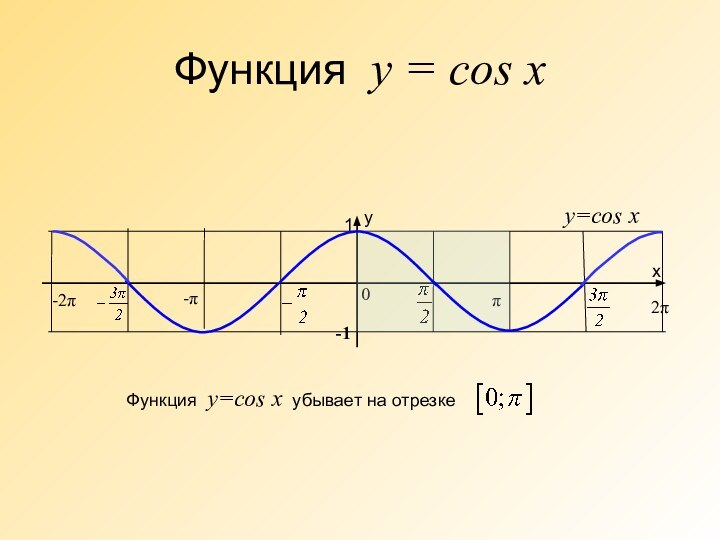
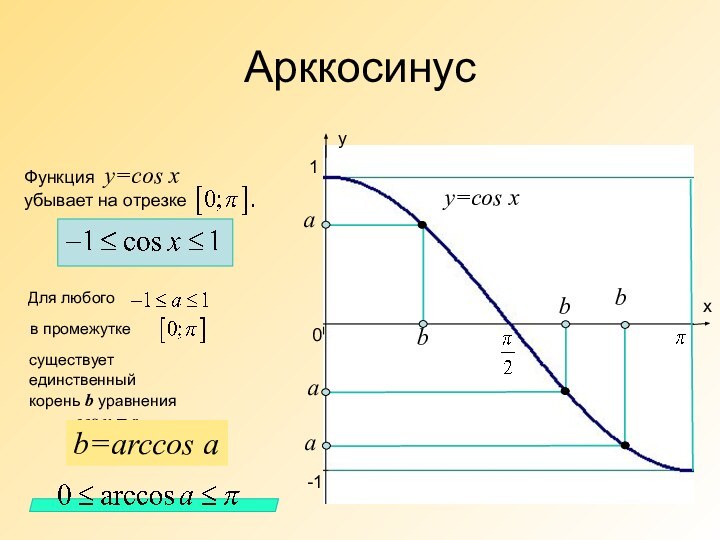

![Презентация по алгебре и начало анализа на тему Арксинус и арккосинус(10 класс) у=arccos x1)Область определения: отрезок [-1; 1]; 2)Область значений: отрезок 3)Функция у =](/img/tmb/6/552060/a736cdb23f7f6622e8491b1715e561e2-720x.jpg)
![Презентация по алгебре и начало анализа на тему Арксинус и арккосинус(10 класс) 2)Область изменения:отрезок[0;π]3)Функция y = arccosx четная:](/img/tmb/6/552060/25e18a8443d4e2b31ba01a48918b3d2a-720x.jpg)