Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему к уроку алгебры в 8 классе по теме Квадратные уравнения

Содержание

№526(а, г)
Проверка домашнего задания Уравнения Решение квадратных уравнений по формуле Р.ДЕКАРТ1596-1650Р.ДЕКАРТ1596-1650И. НЬЮТОН 1643-1727Ф. ВИЕТ1540 -1603 Уравнение общего видаа≠0 Формула корней квадратного уравнения: Рассмотрим три случая: D>0D=0D 1.Если дискриминант больше нуля, т.е. D>0, Формула корней: 2. Если дискриминант равен нулю, т. е. 3. Если дискриминант отрицательный, т.е D Уравнения ВЫВОД:1. Решение квадратных уравнений по формуле корней ВЫВОД:2.Вычислить дискриминант и сравнить его с нулем. ВЫВОД:3. Если D>0 или D=0, то воспользоваться формулой корней.4. Если D САМОСТОЯТЕЛЬНАЯ РАБОТА 1 ВАРИАНТ 2 ВАРИАНТ ПРОВЕРИМ САМОСТОЯТЕЛЬНУЮ РАБОТУ 1 ВАРИАНТ 2 ВАРИАНТ ТЕПЕРЬ ОЦЕНИМ СВОЮ РАБОТУВыполнено одно задание – отметка «3»;Выполнено два задания Домашнее задание:Пункт 21,№ 533, №536, №554(а) Имеет ли корни уравнение Имеет два корня, так как дискриминант положительный
Слайды презентации

Слайд 2

№526(а, г)

№526(а, г)

Слайд 3 Уравнения

Уравнения

Слайд 4 Решение квадратных уравнений по формуле


Решение квадратных уравнений по формуле

Слайд 5 Р.ДЕКАРТ
1596-1650
Р.ДЕКАРТ
1596-1650
И. НЬЮТОН
1643-1727
Ф. ВИЕТ
1540 -1603

Р.ДЕКАРТ1596-1650Р.ДЕКАРТ1596-1650И. НЬЮТОН 1643-1727Ф. ВИЕТ1540 -1603

Слайд 6 Уравнение общего вида

а≠0

Уравнение общего видаа≠0

Слайд 7 Формула корней квадратного уравнения:

Формула корней квадратного уравнения:

Слайд 8

Слайд 9 Рассмотрим три случая:
D>0
D=0
D

Рассмотрим три случая: D>0D=0D

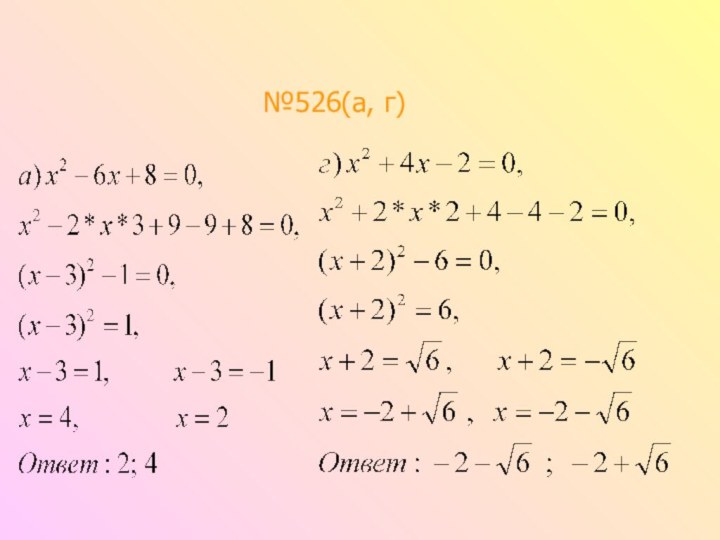
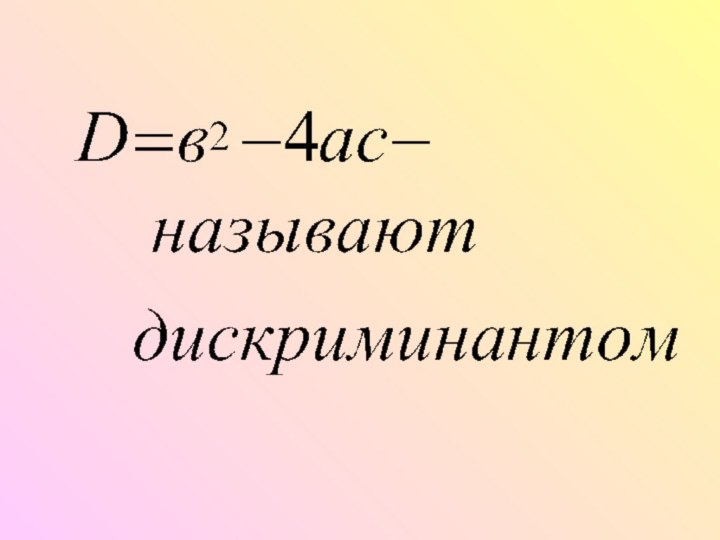
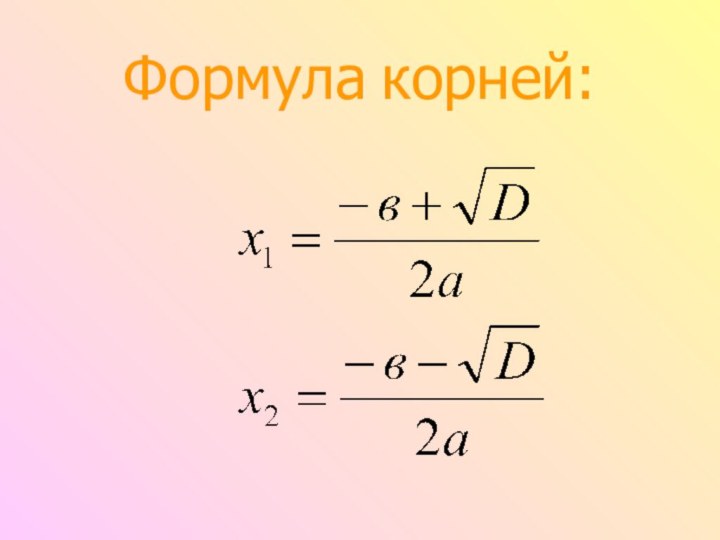
Слайд 10 1.Если дискриминант больше нуля, т.е. D>0,

1.Если дискриминант больше нуля, т.е. D>0, то

то уравнение имеет два различных

корня, которые можно найти по формулам:

Слайд 11 Формула корней:

Формула корней:

Слайд 12 2. Если дискриминант равен нулю, т. е. D=0,

2. Если дискриминант равен нулю, т. е. D=0,

то в этом случае уравнение имеет единственный корень:




Слайд 13 3. Если дискриминант отрицательный, т.е D

3. Если дискриминант отрицательный, т.е D

корней не имеет.

Слайд 14 Уравнения

Уравнения

Слайд 15 ВЫВОД:
1. Решение квадратных

ВЫВОД:1. Решение квадратных уравнений по формуле корней – это

уравнений
по формуле корней – это
общий способ

решения, но иногда быстрее подобрать корни.

Слайд 16 ВЫВОД:
2.Вычислить дискриминант и
сравнить его с нулем.


ВЫВОД:2.Вычислить дискриминант и сравнить его с нулем.

Слайд 17 ВЫВОД:
3. Если D>0 или D=0, то воспользоваться формулой

ВЫВОД:3. Если D>0 или D=0, то воспользоваться формулой корней.4. Если D

корней.

4. Если D

Слайд 18 САМОСТОЯТЕЛЬНАЯ РАБОТА 1 ВАРИАНТ

САМОСТОЯТЕЛЬНАЯ РАБОТА 1 ВАРИАНТ 2 ВАРИАНТ

2 ВАРИАНТ

Слайд 19 ПРОВЕРИМ САМОСТОЯТЕЛЬНУЮ РАБОТУ

ПРОВЕРИМ САМОСТОЯТЕЛЬНУЮ РАБОТУ

Слайд 20 1 ВАРИАНТ 2 ВАРИАНТ

1 ВАРИАНТ 2 ВАРИАНТ

Слайд 21 ТЕПЕРЬ ОЦЕНИМ СВОЮ РАБОТУ
Выполнено одно задание –

ТЕПЕРЬ ОЦЕНИМ СВОЮ РАБОТУВыполнено одно задание – отметка «3»;Выполнено два

отметка «3»;
Выполнено два задания – отметка «3»;
Выполнено три задания

– отметка «4»;
Выполнено четыре задания –
отметка «5».

Слайд 22 Домашнее задание:

Пункт 21,
№ 533, №536, №554(а)

Домашнее задание:Пункт 21,№ 533, №536, №554(а)

Слайд 23 Имеет ли корни уравнение

Имеет ли корни уравнение
  • Имя файла: prezentatsiya-k-uroku-algebry-v-8-klasse-po-teme-kvadratnye-uravneniya.pptx
  • Количество просмотров: 162
  • Количество скачиваний: 0
- Предыдущая Открытое занятие на тему: Да здравствует вежливость и доброта 6 класс
Следующая - Открытый урок по русскому языку Изложение

Похожие презентации

Свойства функций непрерывных на отрезке Свойства функций непрерывных на отрезке 159
Ребусы. Алгебра Ребусы. Алгебра 243
Презентация по математики Взаимное расположение сферы и касательной(11 класс) Презентация по математики Взаимное расположение сферы и касательной(11 класс) 190
Презентация по алгебре на тему: Задачи на движение (7-9 классы) Презентация по алгебре на тему: Задачи на движение (7-9 классы) 163
Сумма n членов прогрессии Сумма n членов прогрессии 170
Задачи на движение Задачи на движение 161
Теория вероятности к экзамену Теория вероятности к экзамену 198
Презентация по Алгебре 7 класс Презентация по Алгебре 7 класс 148
Урок по математике на тему История математики 8 класс Урок по математике на тему История математики 8 класс 177
Презентация по алгебре на тему Степенная функция Презентация по алгебре на тему Степенная функция 150
Функция y=cos x Функция y=cos x 248
Техника дифференцирования. Производная сложной функции Техника дифференцирования. Производная сложной функции 136
Презентация по алгебре 9 класс на тему Арифметическая прогрессия Презентация по алгебре 9 класс на тему Арифметическая прогрессия 148
Презентация по математике на тему Повторение материала за 7 класс Презентация по математике на тему Повторение материала за 7 класс 168
Дидактическая игра Точно в цель на тему Поворот точки вокруг начала координат -3 Дидактическая игра Точно в цель на тему Поворот точки вокруг начала координат -3 131
Презентация к уроку Разложение многочленов на множители с помощью формул сокращенного умножения. (к учебнику А.Г. Мордковича) Презентация к уроку Разложение многочленов на множители с помощью формул сокращенного умножения. (к учебнику А.Г. Мордковича) 167
Презентация по алгебре на тему Применение интеграла Презентация по алгебре на тему Применение интеграла 165
Координатная плоскость Координатная плоскость 129
Нестандартные методы решения неравенст Нестандартные методы решения неравенст 158
Введение понятия множества Введение понятия множества 154
Задачи и упражнения на готовых чертежах Определение и признак параллелограмма Задачи и упражнения на готовых чертежах Определение и признак параллелограмма 216
Презентация по алгебре на тему Метод рационализации при решении логарифмических неравенств Презентация по алгебре на тему Метод рационализации при решении логарифмических неравенств 158
Тригонометрические уравнения. Отбор корней. Алгебра. 10 класс Тригонометрические уравнения. Отбор корней. Алгебра. 10 класс 162
Показательная функция, ее свойства и применение.Показательная функция, ее свойства и применение. Показательная функция, ее свойства и применение.Показательная функция, ее свойства и применение. 191
Применение производной функции Применение производной функции 138
Степень с натуральным показателем Степень с натуральным показателем 138
Разложение на простые множители Разложение на простые множители 171
Численные методы решения уравнений Численные методы решения уравнений 188
Презентация математической игры Кто хочет стать отличником? Презентация математической игры Кто хочет стать отличником? 187
Свойства дифференциала Свойства дифференциала 157