- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике в 7 классе Открытые и закрытые промежутки для проведения эксперимента с числами Нити и бусины
Содержание
- 2. ЗадачаПрофессор истории, изучая старинные документы, обнаружил, что
- 3. ПроблемаКак определить количество натуральных чисел, входящих в промежуток?
- 4. Эксперимент «Нити и бусины»На нить прикрепили бусины.
- 5. 1 группа. Исследование нити с бусинами с
- 6. 2 группа. Исследование нити с бусинами на
- 7. 3 группа. Исследование замкнутой нити с бусинами.
- 8. Сколько столбов?Для того, чтобы перегородить опасный участок,
- 9. Задачи 1 группыЗадача 1. Из куска ткани
- 10. Задача 2.Имеются много брёвен длиной 4 м
- 11. Сколько флажков?Обозначим скрепки точками: скрепок – 7,
- 12. Задачи 2 группы.1.Сколько столбов нужно установить на
- 13. Задача 2. Есть часы, которые в 3
- 14. Задачи 3 группы.Задача 1.Велосипедисты отправились в поход.
- 15. Задача 2.Сколько стоек нужно для ограждения земельного
- 16. Задача 3.На колесе длиной 1,5 м нужно
- 17. Вернёмся к нашей задаче.Решение.Задание на количество чисел
- 18. Промежутки и целые числа Сколько целых чисел
- 19. Разрезаем верёвкуНа верёвке отмечены поперечные линии синего,
- 20. Задачи для размышлений в группахРешите задачу с
- 21. Линии на воздушном шареНа поверхности воздушного шара
- 22. Скачать презентацию
- 23. Похожие презентации
ЗадачаПрофессор истории, изучая старинные документы, обнаружил, что в одном из документов утеряны некоторые листы. Номер последней пронумерованной страницы – 98, а следующая часть начинается со страницы 131. Сколько листов утеряно?




















Слайд 4
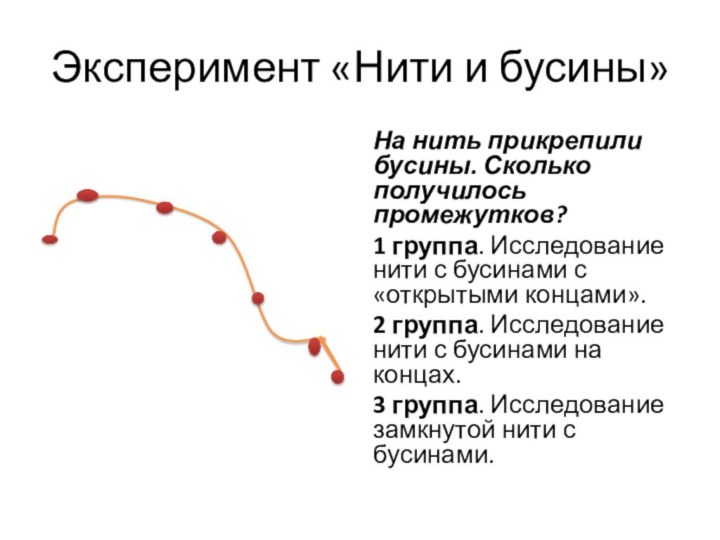
Эксперимент «Нити и бусины»
На нить прикрепили бусины. Сколько
получилось промежутков?
1 группа. Исследование нити с бусинами с «открытыми
концами».2 группа. Исследование нити с бусинами на концах.
3 группа. Исследование замкнутой нити с бусинами.
Слайд 5 1 группа. Исследование нити с бусинами с «открытыми
концами».
Цель: определить связь между количеством бусин на нити и
промежутков.Задача: вывести формулу связи количества бусин и промежутков.
Ход исследования.
На нити размещать несколько бусин и подсчитывать количество промежутков. Результаты заносим в таблицу.
Вывод: количество бусин на 1 меньше, чем промежутков.
Формула: Б + 1 = П.
Слайд 6
2 группа. Исследование нити с бусинами на концах.
Цель:
определить связь между количеством бусин на нити и промежутков.
Задача:
вывести формулу связи количества бусин и промежутков.Ход исследования.
На нити разместить несколько бусин и подсчитывать количество промежутков. Результаты заносим в таблицу.
Вывод: количество бусин на 1 больше, чем промежутков.
Формула: Б - 1 = П.
Слайд 7
3 группа. Исследование замкнутой нити с бусинами.
Цель: определить
связь между количеством бусин на нити и промежутков.
Задача: вывести
формулу связи количества бусин и промежутков.Ход исследования.
На нити разместить несколько бусин и подсчитывать количество промежутков. Результаты заносим в таблицу.
Вывод: количество бусин равно числу промежутков.
Формула: Б = П.
Слайд 8
Сколько столбов?
Для того, чтобы перегородить опасный участок, необходимо
поставить ограждение из готовых блоков длиной 18 м. Длина
каждого блока 3 м. Сколько столбов нужно поставить для такого забора?Какого типа эта задача?
Посмотрим на ограждение сверху: это отрезок, а столбы – точки.
18:3=6 (промежутков)
6+1=7 (столбов)
Слайд 9
Задачи 1 группы
Задача 1. Из куска ткани 12
м решили сшить 4 костюма. На 1 костюм расходуется
3 м. Сколько разрезов ткани произведено?Решение.
12:3 = 4 (отрезка)
4-1 = 3 (разреза)
Слайд 10
Задача 2.
Имеются много брёвен длиной 4 м и
5 м одинаковой толщины. Бревно перепиливается за 1 минуту.
Надо напилить 20 метровых чурбаков. Какие брёвна пилить быстрее?Решение.
Из 4-хметровых брёвен - 15 распилов,
из 5-метровых – 16 распилов.
Ответ: 4-х метровые пилить быстрее.
Слайд 11
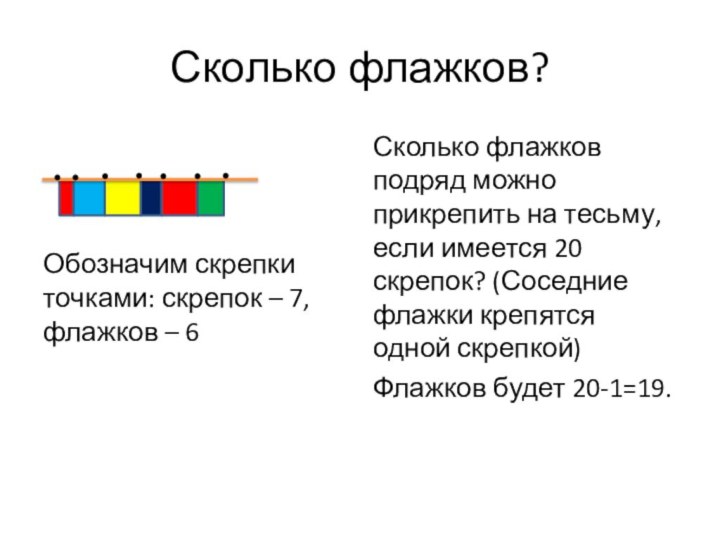
Сколько флажков?
Обозначим скрепки точками: скрепок – 7, флажков
– 6
Сколько флажков подряд можно прикрепить на тесьму, если
имеется 20 скрепок? (Соседние флажки крепятся одной скрепкой)Флажков будет 20-1=19.
Слайд 12
Задачи 2 группы.
1.Сколько столбов нужно установить на расстоянии
2 км, если между столбами 50 м?
Решение.
2000 :
50 = 40 (промежутков)40+1=41 (столб)
Ответ: 41 столб.
Слайд 13 Задача 2. Есть часы, которые в 3 часа
бьют в течение 8 с. Сколько секунд будут бить
часы в 6 часов?8:2=4 (с)
5 х 4= 20 (с).
Ответ: 20 с будут бить часы в 6 часов.
Слайд 14
Задачи 3 группы.
Задача 1.
Велосипедисты отправились в поход. Каждые
сутки они останавливались на ночлег в каком-нибудь селении. Через
5 дней они вернулись домой. Сколько раз ночевали велосипедисты в чужих селениях?
Слайд 15
Задача 2.
Сколько стоек нужно для ограждения земельного участка
прямоугольной формы, размером 120 на 60 м, если между
столбами 3 м?Решение.
Р = (120+60)х2=360 (м)
360:3=120 (промежутков)
Ответ: 120 стоек.
Слайд 16
Задача 3.
На колесе длиной 1,5 м нужно установить
спицы на расстоянии 3 см друг от друга. Сколько
спиц необходимо?50
Слайд 17
Вернёмся к нашей задаче.
Решение.
Задание на количество чисел в
открытом промежутке.
131 – 98 = 33
33 – 1
= 32 (страницы)32 : 2 = 16 (листов)
Ответ: 16 листов утеряно.
Слайд 18
Промежутки и целые числа
Сколько целых чисел между числами
– 16 и 12?
Решение.
12 – (- 16) – 1
= 27 чисел (28 единичных промежутков и 27 чисел).2. Сколько решений имеет неравенство
16 ≤ х ≤ 12?
28 единичных промежутков, 28 + 1 число.
Слайд 19
Разрезаем верёвку
На верёвке отмечены поперечные линии синего, розового
и фиолетового цветов. Если разрезать верёвку по синим линиям,
то получится 5 кусков, если по розовым – 7 кусков, по фиолетовым – 11 кусков. Сколько получится кусков верёвки, если её разрезать по всем линиям? (Разрезы не совпадают)Решение.
Разрезов меньше, чем кусков на 1. Складываем все разрезы:
4 + 6 + 10 = 20 (разрезов)
20 + 1 = 21 (кусок)
Ответ: 21 кусок получится.
Слайд 20
Задачи для размышлений в группах
Решите задачу с цветными
линиями на верёвке для случая, когда линии одного цвета
находятся на одинаковом расстоянии друг от друга и разрезы могут совпадать. Длина верёвки – 385 см.Решение.
385 = 5х7х11 (5, 7 и 11 – простые числа); куски при наложении совпадут, если:
НОК(5;7)=35 – кусков нужно для совпадения или
НОК(7;11)=77 – кусков нужно для совпадения или
НОК(5;11)=55 – кусков нужно для совпадения.
Такого количества кусков нет по условию задачи.
Совпадений нет.
Ответ: 21 кусок получится.
Слайд 21
Линии на воздушном шаре
На поверхности воздушного шара проведены
10 линий, проходящих через 2 точки, и 20 линий,
параллельных друг другу. На сколько частей разделилась поверхность воздушного шара?Решение.
Линии, проходящие через 2 точки, разделят шар на 10 частей.
20 параллельных линий разделит шар на 20+1 часть.
10х21=210 частей получится.





























