- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре Квадратные уравнения (8 класс)
Содержание
- 2. Если ты услышишь, что кто-то не любит
- 3. Уравнение вида ах2 + вх +с =
- 4. 1. 2. 3. 4. 5. 6. 7. ФОРМУЛЫ
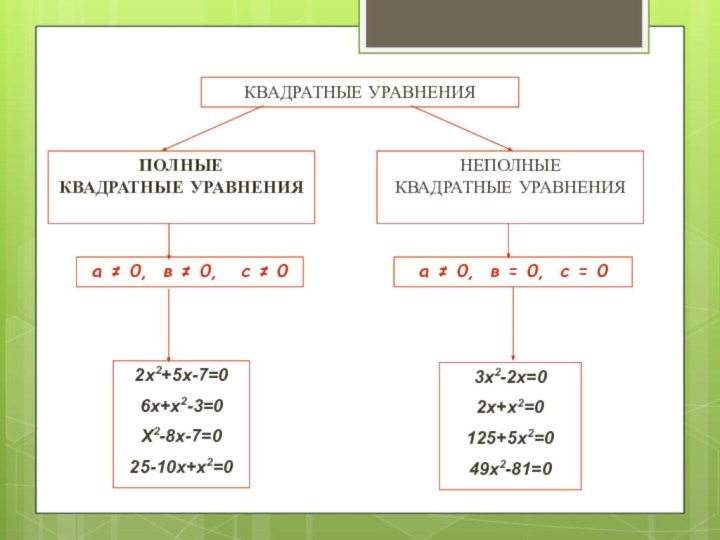
- 5. ПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯНЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯКВАДРАТНЫЕ УРАВНЕНИЯа ≠
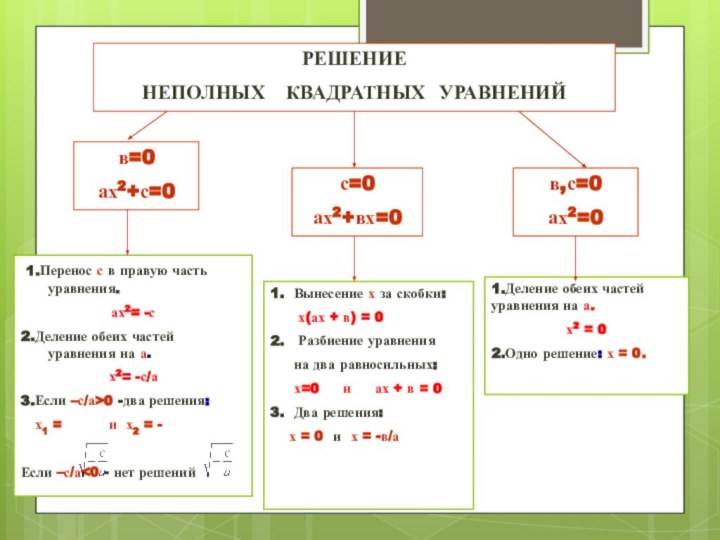
- 6. РЕШЕНИЕ НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙв=0ах2+с=0с=0ах2+вх=0в,с=0ах2=0 1.Перенос с
- 7. СПОСОБЫ РЕШЕНИЯ ПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙВыделение квадрата двучлена.Формула: D = b2- 4ac, x1,2=Теорема Виета.
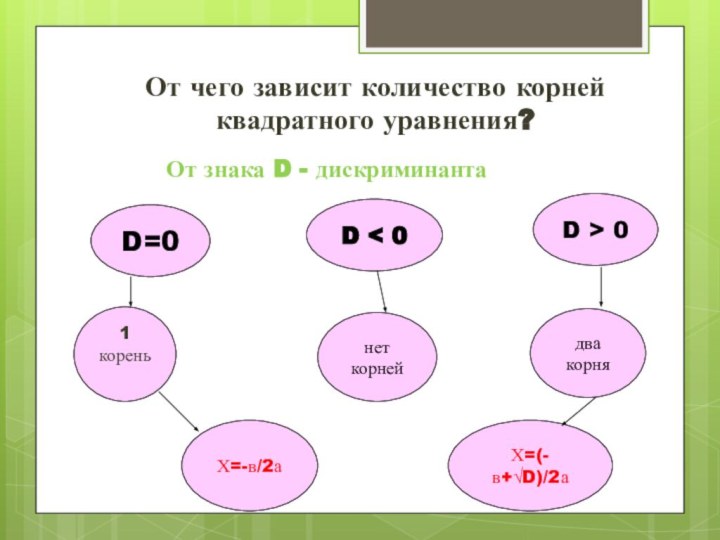
- 8. От чего зависит количество корней квадратного уравнения?От знака D - дискриминанта
- 9. Впервые квадратное уравнение сумели решить
- 10. Метод извлечения квадратного корня с
- 11. Аль – Хорезми — арабский учёный, который
- 12. БХАСКАРА (1114—1185, обычно называемый Бхаскарой
- 13. 1). Если а + в +с =
- 14. Скачать презентацию
- 15. Похожие презентации
Если ты услышишь, что кто-то не любит математику, не верь. Её нельзя не любить - её можно только не знать.











Слайд 3
Уравнение вида ах2 + вх +с = 0,
где х –переменная,
а, в и с
некоторые числа,причем а ≠ 0 .
ОПРЕДЕЛЕНИЕ:
Квадратным уравнением называется
Слайд 5
ПОЛНЫЕ
КВАДРАТНЫЕ УРАВНЕНИЯ
НЕПОЛНЫЕ
КВАДРАТНЫЕ УРАВНЕНИЯ
КВАДРАТНЫЕ УРАВНЕНИЯ
а ≠ 0, в ≠
0, с ≠ 0
а ≠ 0, в =
0, с = 02х2+5х-7=0
6х+х2-3=0
Х2-8х-7=0
25-10х+х2=0
3х2-2х=0
2х+х2=0
125+5х2=0
49х2-81=0
Слайд 6
РЕШЕНИЕ
НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙ
в=0
ах2+с=0
с=0
ах2+вх=0
в,с=0
ах2=0
1.Перенос с в
правую часть уравнения.
ах2= -с
2.Деление обеих частей уравнения на а.
х2=
-с/а3.Если –с/а>0 -два решения:
х1 = и х2 = -
Если –с/а<0 - нет решений
1. Вынесение х за скобки:
х(ах + в) = 0
2. Разбиение уравнения
на два равносильных:
х=0 и ах + в = 0
3. Два решения:
х = 0 и х = -в/а
1.Деление обеих частей уравнения на а.
х2 = 0
2.Одно решение: х = 0.
Слайд 7
СПОСОБЫ РЕШЕНИЯ
ПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙ
Выделение квадрата двучлена.
Формула: D
= b2- 4ac, x1,2=
Теорема Виета.
Слайд 9 Впервые квадратное уравнение сумели решить математики
Древнего Египта. В одном из математических папирусов содержится задача:
«Найти стороны поля, имеющего форму прямоугольника,
если его площадь 12, а – длины равны ширине».
«Длина поля равна 4», – указано в папирусе.
история квадратных уравнений
Слайд 10 Метод извлечения квадратного корня с помощью
формулы квадрата суммы двух чисел получил название
«тянь-юань»
(буквально
– «небесный элемент») – так китайцы обозначали неизвестную величину
Математика в девяти книгах (начало)
Слайд 11
Аль – Хорезми —
арабский учёный, который
в 825 г. написал книгу
«Книга о восстановлении и противопоставлении».
Это был первый в мире учебник алгебры. Он также дал шесть видов квадратных уравнений и для каждого из шести уравнений в словесной форме сформулировал особое правило его решения.
Слайд 12
БХАСКАРА
(1114—1185,
обычно называемый Бхаскарой II,
чтобы отличить его от другого индийского учёного Бхаскары I)
—крупнейший индийский математик и астроном XII века.
Бхаскара получал отрицательные корни уравнений,
хотя и сомневался в их значимости. Ему принадлежит один из самых ранних проектов вечного двигателя.
Слайд 13 1). Если а + в +с = 0,
то х1 = 1; х2 = с/а
2).Если
а + с = в , то х1 = -1; и х2 = - с/а(свойства коэффициентов квадратных уравнений)
ТАЙНЫ КОРНЕЙ КВАДРАТНЫХ УРАВНЕНИЙ