- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Построение графика квадратичной функции (8 класс)
Содержание
- 2. повторение
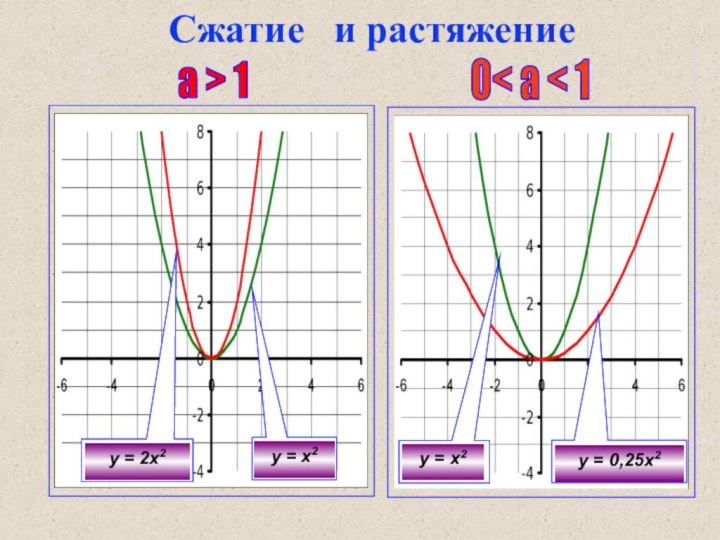
- 3. а > 10< а < 1у =
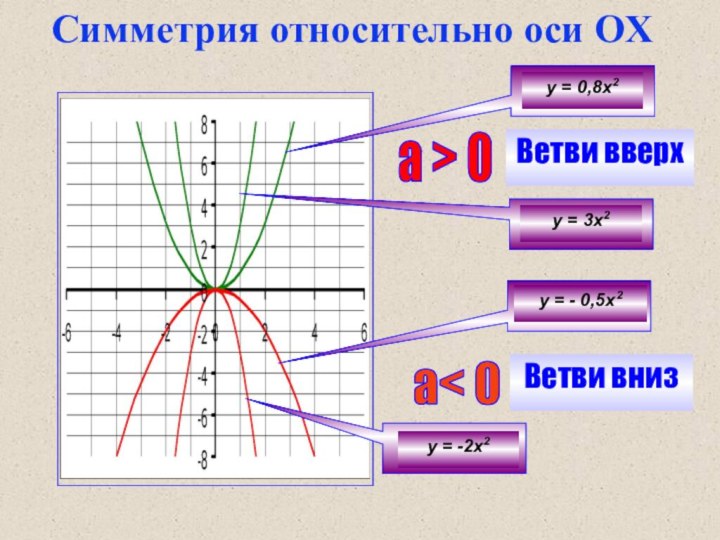
- 4. Ветви вверха > 0а< 0Ветви внизу =
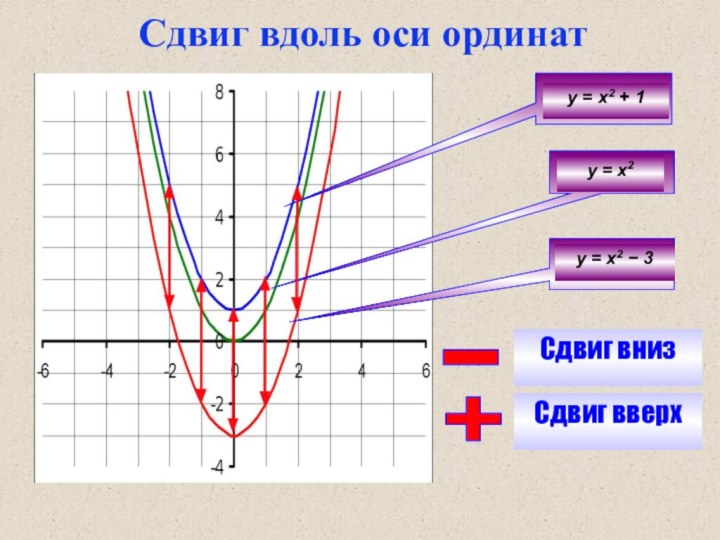
- 5. у = х2у = х2 3у = х2 + 1Сдвиг вниз-Сдвиг вверх+Сдвиг вдоль оси ординат
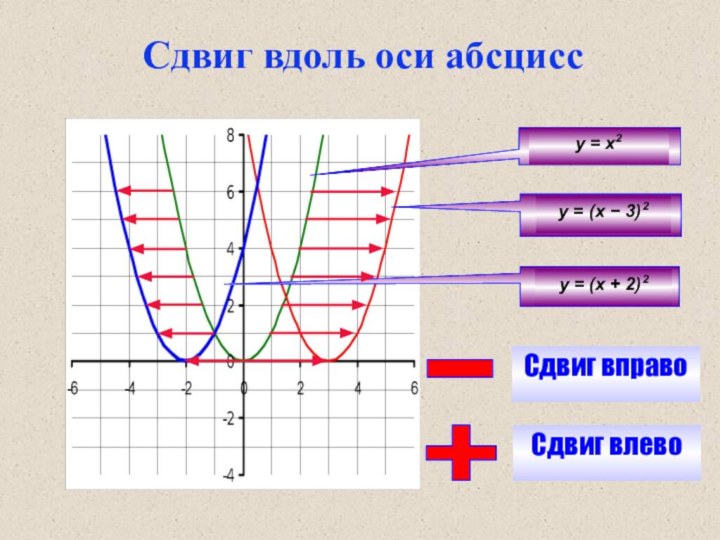
- 6. у = х2у = (х 3)2у = (х + 2)2Сдвиг вправо-Сдвиг влево+Сдвиг вдоль оси абсцисс
- 7. у = а(х - m)2 + nу
- 8. Квадратичной функцией называется функция, которую можно задать
- 9. Графиком квадратичной функции является парабола, ветви которой
- 10. Чтобы построить график функции надо:1. Описать функцию:
- 11. Чтобы построить график функции надо:2. Найти координаты
- 12. Чтобы построить график функции надо:3. Заполнить таблицу
- 13. Чтобы построить график функции надо:4. Построить график
- 14. Построить в тетради график функции у = -2х²+8х-3
- 15. Постройте график функции у = -2х²+8х-3
- 16. Проверьте себя. у = -2х²+8х-3 - квадратичная
- 17. Рассмотрим свойства этой квадратичной функции. Область
- 18. В классе:№ 22.1 (а, б) – 22.4
- 19. Скачать презентацию
- 20. Похожие презентации









Слайд 4
Ветви вверх
а > 0
а< 0
Ветви вниз
у = -
0,5х2
у = -2х2
у = 3х2
у =
0,8х2 Симметрия относительно оси OX
Слайд 7
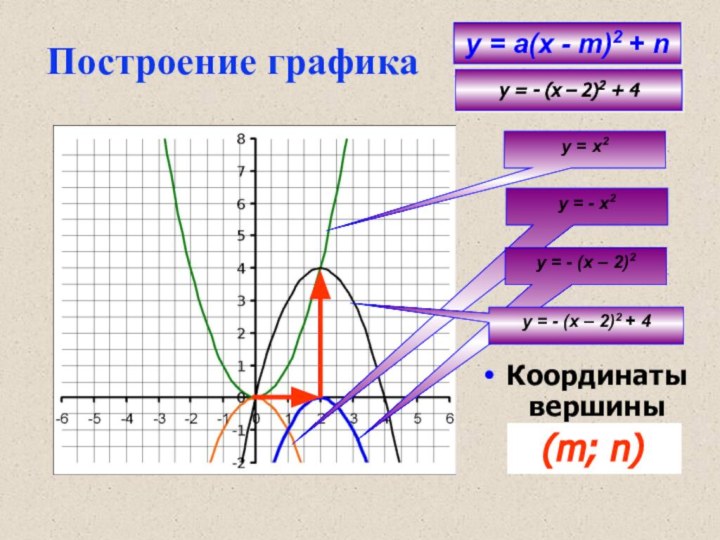
у = а(х - m)2 + n
у =
х2
у = - х2
у = - (х – 2)2
у
= - (х – 2)2 + 4у = - (х – 2)2 + 4
Построение графика
Координаты вершины
…
(2; 4)
(m; n)
Слайд 8 Квадратичной функцией называется функция, которую можно задать формулой
вида y=ax²+bx+c, где х - независимая переменная, a,
b и с -некоторые числа (причём а≠0).Например: у = 5х²+6х+3,
у = -7х²+8х-2,
у = 0,8х²+5,
у = ¾х²-8х,
у = -12х²
- квадратичные функции
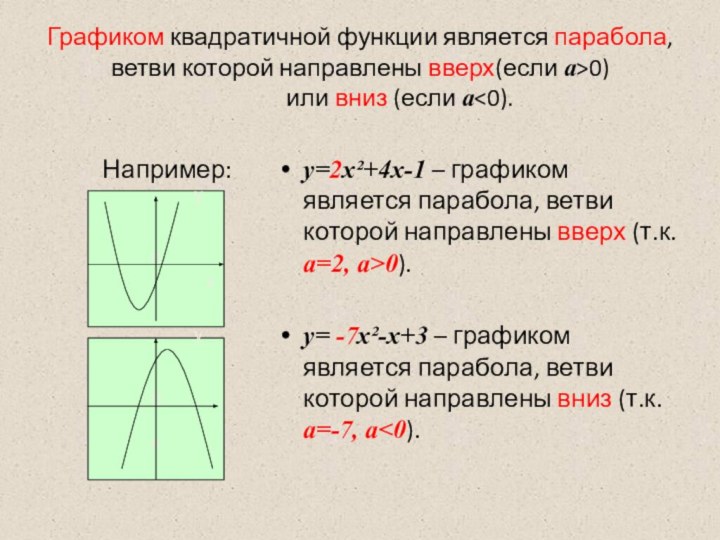
Слайд 9 Графиком квадратичной функции является парабола, ветви которой направлены
вверх(если а>0)
или вниз (если а<0). Например:
у=2х²+4х-1 – графиком является парабола, ветви которой направлены вверх (т.к. а=2, а>0).
у= -7х²-х+3 – графиком является парабола, ветви которой направлены вниз (т.к. а=-7, а<0).
у
0
х
у
0
х
Слайд 10
Чтобы построить график функции надо:
1. Описать функцию:
название
функции,
что является графиком функции,
куда направлены ветви параболы.
Пример: у =
х²-2х-3 – квадратичная функция, графиком является парабола, ветви которой направлены вверх (т.к. а=1, а>0)
Слайд 11
Чтобы построить график функции надо:
2. Найти координаты вершины
параболы А(m;n) по формулам:
;или n = у(m) т.е. подставить найденное значение абсциссы m в формулу, которой задана функция и вычислить значение.
Прямая x=m является осью симметрии параболы.
Пример: у = х²-2х-3 (а = 1; b = -2; с = -3) Найдём координаты вершины параболы
n = 1²-2·1-3 = -4
А(1;-4) – вершина параболы.
х=1 – ось симметрии параболы.
Слайд 12
Чтобы построить график функции надо:
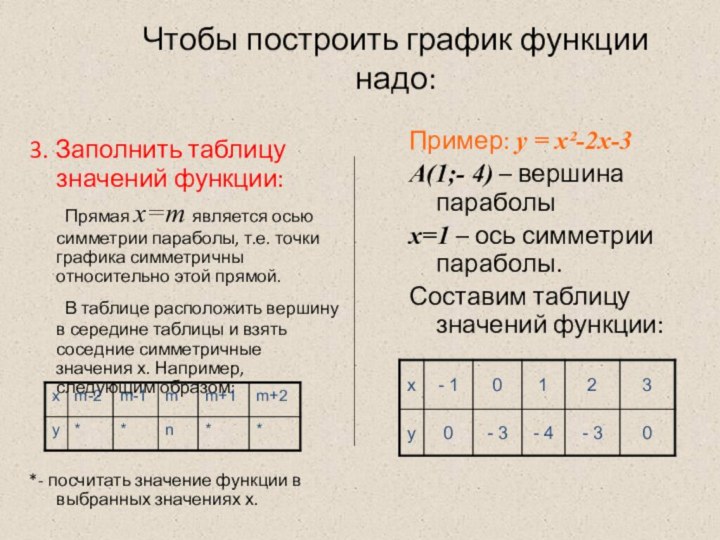
3. Заполнить таблицу значений
функции:
Прямая x=m является осью симметрии параболы, т.е. точки
графика симметричны относительно этой прямой.В таблице расположить вершину в середине таблицы и взять соседние симметричные значения х. Например, следующим образом:
*- посчитать значение функции в выбранных значениях х.
Пример: у = х²-2х-3
А(1;- 4) – вершина параболы
х=1 – ось симметрии параболы.
Составим таблицу значений функции:
Слайд 13
Чтобы построить график функции надо:
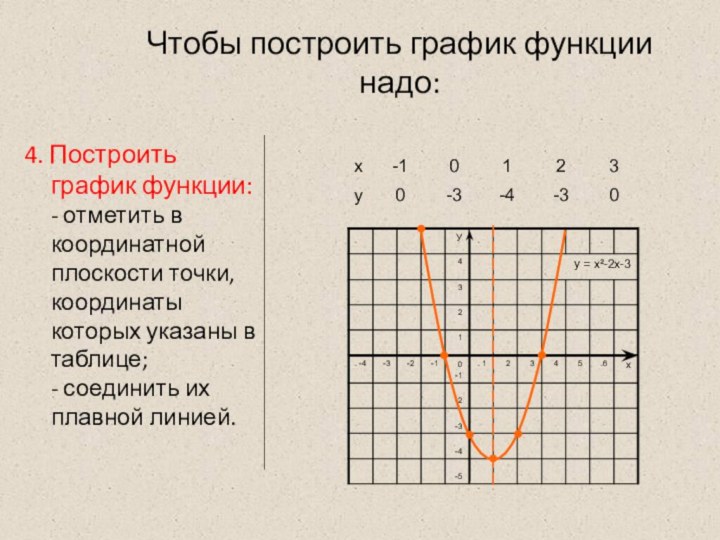
4. Построить график функции:
-
отметить в координатной плоскости точки, координаты которых указаны в таблице; - соединить их плавной линией.Слайд 15 Постройте график функции у = -2х²+8х-3 План построения
графика квадратичной функции:
1. Описать функцию:
название функции;
что является
графиком функции;куда направлены ветви параболы
2. Найти координаты вершины параболы А(m;n)
по формулам:
или n = у(m)
3. Заполнить таблицу значений функции.
4. Построить график функции:
отметить в координатной плоскости точки, координаты которых указаны в таблице;
соединить их плавной линией.
Слайд 16
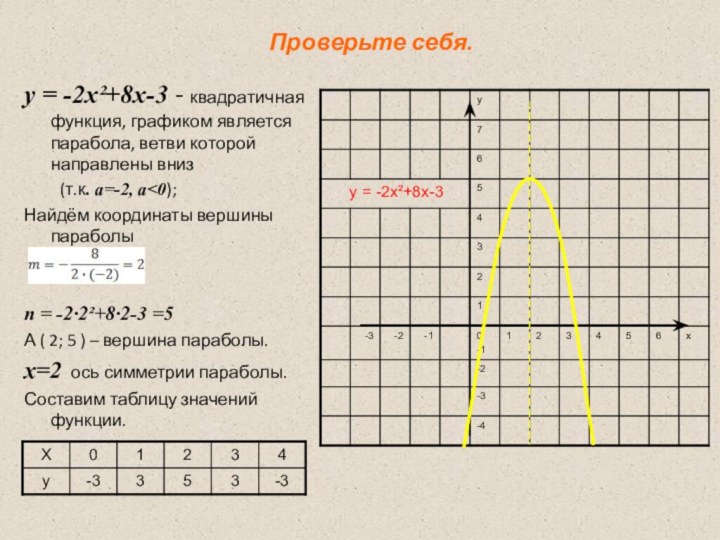
Проверьте себя.
у = -2х²+8х-3 - квадратичная функция,
графиком является парабола, ветви которой направлены вниз
(т.к. а=-2,
а<0);Найдём координаты вершины параболы
n = -2·2²+8·2-3 =5
А ( 2; 5 ) – вершина параболы.
х=2 ось симметрии параболы.
Составим таблицу значений функции.
Слайд 17
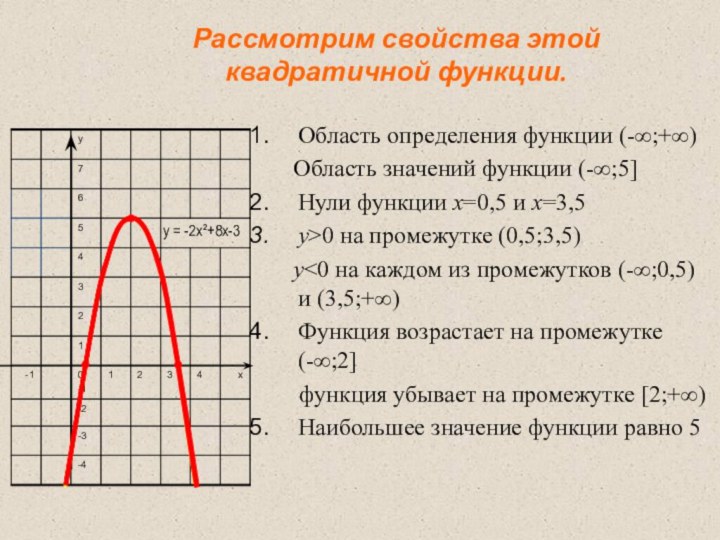
Рассмотрим свойства этой квадратичной функции.
Область определения функции
(-∞;+∞)
Область значений функции (-∞;5]
Нули функции х=0,5 и х=3,5
у>0 на
промежутке (0,5;3,5) y<0 на каждом из промежутков (-∞;0,5) и (3,5;+∞)
Функция возрастает на промежутке (-∞;2]
функция убывает на промежутке [2;+∞)
Наибольшее значение функции равно 5





























