Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Исследовательская работа по теме: Квадратные уравнения

Содержание

Цель: Изучить устные приёмы эффективного решения квадратных уравнений.
Исследовательская работа по теме: «Квадратные уравнения».Муниципальное общеобразовательное учреждение«Средняя общеобразовательная школа №2 п. Цель: Изучить устные приёмы эффективного решения квадратных уравнений. Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные 1 корень: x = 02корня, если: а и с имеют разные знакиНет D >0D =0D Теоремы Приёмы устного решения квадратного уравнения 1) 2 ) приём «коэффициентов»3) приём «переброски» Приём «Коэффициентов»:1) Если а+в+с=0, то 2) Если в = а + с, Приёмы устного решения решения квадратныхуравнений , тоНапример:Если Приём №1 приём №2Если b = a + c, тоПриём №2Например: Решаем устно Его корни 10 и 1, и делим на 2. Ответ: 5;Приём №3 5) Например, 4)Например:Например: 7)6)Например:Например: Квадратные уравнения с большими коэффициентами1.2.3.4. По праву достойна в стихах быть воспета свойствах корней теорема Виета. Что Выводы: данные приёмы решения заслуживают внимания, поскольку они не отражены
Слайды презентации

Слайд 2
Цель:


Изучить устные
приёмы эффективного
решения квадратных

Цель: Изучить устные приёмы эффективного решения квадратных уравнений.

уравнений.

Слайд 3 Квадратные уравнения – это фундамент, на котором покоится

Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры.

величественное здание алгебры. Квадратные уравнения находят широкое применение при

решении тригонометрических,
показательных , иррациональных уравнений и неравенств.
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения.
Однако имеются и другие приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения.


Приобретать знания - храбрость Приумножать их - мудрость А умело применять великое искусство

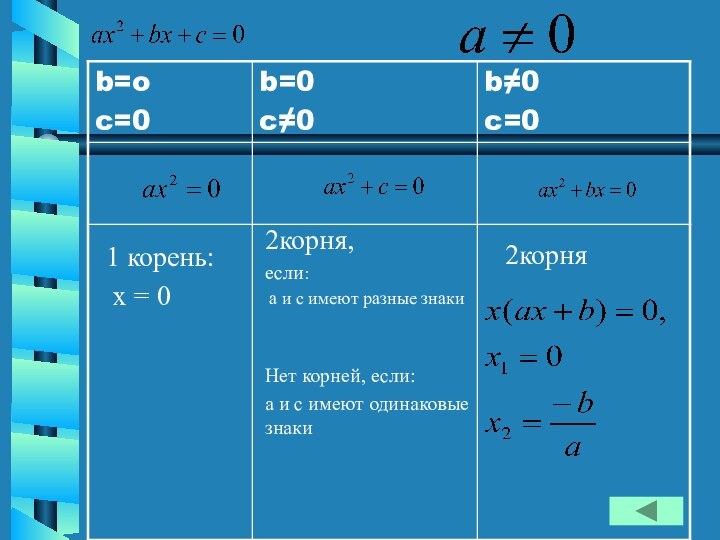
Слайд 4
1 корень:
x = 0

2корня,
если:
а и

1 корень: x = 02корня, если: а и с имеют разные

с имеют разные знаки


Нет корней, если:
а и с имеют

одинаковые знаки



2корня


Слайд 5 D >0
D =0
D

D >0D =0D

Слайд 6 Теоремы


Теоремы

Слайд 7 Приёмы устного решения квадратного уравнения
1) 2 )

Приёмы устного решения квадратного уравнения 1) 2 ) приём «коэффициентов»3) приём «переброски»

приём «коэффициентов»
3) приём «переброски»

Слайд 8
Приём «Коэффициентов»:
1) Если а+в+с=0, то
2) Если в

Приём «Коэффициентов»:1) Если а+в+с=0, то 2) Если в = а +

= а + с, то
3) Если
Используя приёмы 1)

-3) можно придумывать
уравнения с рациональными корнями.

, то приём «Переброски»

Слайд 9 Приёмы устного решения решения квадратных
уравнений


Приёмы устного решения решения квадратныхуравнений , тоНапример:Если Приём №1


, то

Например:



Если
Приём №1

Слайд 10
приём №2
Если b = a + c,

приём №2Если b = a + c, тоПриём №2Например:

то
Приём №2

Например:

Слайд 11 Решаем устно
Его корни 10 и 1,

Решаем устно Его корни 10 и 1, и делим на 2. Ответ: 5;Приём №3

и делим на 2.
Ответ: 5;
Приём №3

Слайд 12 5)

Например,

4)
Например:
Например:

5) Например, 4)Например:Например:

Слайд 13 7)



6)


Например:
Например:

7)6)Например:Например:

Слайд 14
Квадратные уравнения с большими коэффициентами


1.
2.
3.




4.

Квадратные уравнения с большими коэффициентами1.2.3.4.

Слайд 15
По праву достойна в стихах быть воспета свойствах

По праву достойна в стихах быть воспета свойствах корней теорема Виета.

корней теорема Виета.
Что лучше, скажи, постоянства такого:
Умножишь ты

корни – и дробь уж готова?
В числителе с , в знаменателе а.
А сумма корней тоже дроби равна.
Хоть с минусом дробь, что за беда.
В числителе в, в знаменателе а.

Это интересно

  • Имя файла: issledovatelskaya-rabota-po-teme-kvadratnye-uravneniya.pptx
  • Количество просмотров: 69
  • Количество скачиваний: 0
- Предыдущая Гендерная педагогика как эффективный путь социализации и повышения качества обучения и развития учащихся
Следующая - Презентация: Памятники Парка Победы

Похожие презентации

Презентация по математике на темуТеория вероятности,статистика, комбинаторика (9 класс) Презентация по математике на темуТеория вероятности,статистика, комбинаторика (9 класс) 164
Шаблоны презентаций Математика - 18 Шаблоны презентаций Математика - 18 151
ЦОР по теории вероятностей ЦОР по теории вероятностей 253
Математические диктанты по теме Квадратные уравнения Математические диктанты по теме Квадратные уравнения 278
Урок-презентация для 7 класса по теме: Уравнения Урок-презентация для 7 класса по теме: Уравнения 189
Комбинаторика Комбинаторика 144
Производная функции Производная функции 149
Презентация по математике на тему Системы рациональных уравнений (11 класс) Презентация по математике на тему Системы рациональных уравнений (11 класс) 189
Определение параллельных прямых Определение параллельных прямых 148
Презентация по алгебре на тему Простейшие тригонометрические уравнения (10 класс) Презентация по алгебре на тему Простейшие тригонометрические уравнения (10 класс) 163
Ох уж эти показательные… Решение показательных уравнений и неравенств Ох уж эти показательные… Решение показательных уравнений и неравенств 185
Урок алгебры в 9 классе Урок алгебры в 9 классе 142
Презентация Чертежи к задачам (треугольники) Презентация Чертежи к задачам (треугольники) 149
Презентация по алгебре :Открытый урок по теме: Арифметическая и геометрическая прогрессии.(9 класс) Презентация по алгебре :Открытый урок по теме: Арифметическая и геометрическая прогрессии.(9 класс) 186
Тригонометрические формулы (10 класс) Тригонометрические формулы (10 класс) 322
Презентация по математики Внеклассное мероприятие Математический лабиринт (10 класс) Презентация по математики Внеклассное мероприятие Математический лабиринт (10 класс) 213
Основы тригонометрии Основы тригонометрии 199
Презентация по математике на тему Лидер 21 века Презентация по математике на тему Лидер 21 века 189
Презентация по математике на тему Решение логарифмических уравнений Презентация по математике на тему Решение логарифмических уравнений 133
Определение квадратного уравнения. Неполные квадратные уравнения Определение квадратного уравнения. Неполные квадратные уравнения 144
Презентация по математике на тему Решение тригонометрических уравнений с отбором корней Презентация по математике на тему Решение тригонометрических уравнений с отбором корней 174
Презентация по алгебре на темуСвязь между коэффициентами и корнями квадратного уравнения(8класс) Презентация по алгебре на темуСвязь между коэффициентами и корнями квадратного уравнения(8класс) 202
Методы решения иррациональных уравнений Методы решения иррациональных уравнений 229
Производная сложной функции Производная сложной функции 134
Теорема об отрезках пересекающихся хорд Теорема об отрезках пересекающихся хорд 234
Арифметическая и геометрическая прогрессии Повторение Арифметическая и геометрическая прогрессии Повторение 83
8 класс Квадратные уравнения 8 класс Квадратные уравнения 165
Презентация к уроку алгебры в 11 классе на тему Свойства логарифма Презентация к уроку алгебры в 11 классе на тему Свойства логарифма 185
Презентация по алгебре на тему Арксинус Презентация по алгебре на тему Арксинус 163
Презентация по алгебре Корень n-ой степени Презентация по алгебре Корень n-ой степени 175