Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по алгебре на тему Классификация квадратных уравнений и уравнений, приводимых к квадратным

Содержание

Квадратное уравнениеКвадратным называют алгебраическое уравнение 2-ой степени, т.е. уравнение вида ax²+bx+c=0, где а≠0. (1)
Классификация квадратных уравнений и уравнений, приводимых к квадратным учитель математики Квадратное уравнениеКвадратным называют алгебраическое уравнение 2-ой степени, т.е. уравнение вида ax²+bx+c=0, где а≠0. 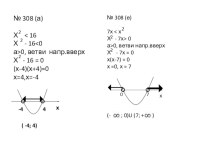(1) с помощью дискриминанта с помощью теоремы Виета графический способ разложение на множителипо РешениеРешим квадратное уравнение x²-5x+4=0С помощью дискриминантаD=b²-4ac D=5²-4*4*1=9 Решение Решим с помощью теоремы Виета: Решение Решим уравнение x²-5x+4=0 . Графическим способом.у4ух01y= x2 -5x+4y =0 РешениеРешим уравнение разложением на множители: Решение Решим это уравнение по коэффициентам: Если a+b+c=0, то РешениеРешим уравнение выделением квадратадвучлена: Уравнения приводящиеся к квадратнымБиквадратныеСимметричныеОднородные Возвратные или обобщенно-симметрическиеЛогарифмическиеПоказательныеТригонометрические Уравнения приводящиеся к квадратным 1.Биквадратное уравнение сводится к квадратному заменой x² переменной y. Уравнения приводящиеся к квадратным3.Уравнение сводится к квадратному уравнению заменой Уравнения приводящиеся к квадратным4.Вообще, замена Уравнения приводящиеся к квадратным 6. Уравнение «симметричное» относительно Основные способы решения уравнений приводящихся к квадратным уравнениям Замена переменной Разложением на Решение квадратных уравнений и приводящихся к ним. x4+ 4 x2 –21 Решение квадратных уравнений и приводящихся к ним. Однородное уравнение относительно Решение квадратных уравнений и приводящихся к ним. ОДЗ: Пусть Решение квадратных уравнений и приводящихся к ним.t2 – 6t + 1 = Решение квадратных уравнений и приводящихся к ним.Ответ: х = 0, 1 а2 . ОДЗ:≠Ответ:Решение квадратных уравнений и приводящихся к ним. С П А С И Б О З А В Н
Слайды презентации

Слайд 2 Квадратное уравнение
Квадратным называют алгебраическое уравнение 2-ой степени, т.е.

Квадратное уравнениеКвадратным называют алгебраическое уравнение 2-ой степени, т.е. уравнение вида ax²+bx+c=0, где а≠0. (1)

уравнение вида
 
ax²+bx+c=0, где а≠0. (1)









Слайд 3








с помощью дискриминанта
с помощью теоремы Виета

с помощью дискриминанта с помощью теоремы Виета графический способ разложение на

графический способ
разложение на множители
по коэффициентам
выделением квадрата двучлена
Основные способы

решения
квадратных уравнений

Слайд 4 Решение












Решим квадратное уравнение x²-5x+4=0
С помощью дискриминанта
D=b²-4ac
D=5²-4*4*1=9




РешениеРешим квадратное уравнение x²-5x+4=0С помощью дискриминантаD=b²-4ac D=5²-4*4*1=9


Слайд 5







Решение

Решим с помощью теоремы Виета:

Решение Решим с помощью теоремы Виета:

Слайд 6 Решение
Решим уравнение x²-5x+4=0 .

Решение Решим уравнение x²-5x+4=0 . Графическим способом.у4ух01y= x2 -5x+4y =0

Графическим способом.







у
4
у
х
0
1

y= x2 -5x+4
y =0

Слайд 7 Решение
Решим уравнение разложением на множители:








РешениеРешим уравнение разложением на множители:

Слайд 8 Решение
 Решим это уравнение по коэффициентам:

Если a+b+c=0, то

Решение Решим это уравнение по коэффициентам: Если a+b+c=0, то

Если a-b+c=0, то
 


 
 
 








Слайд 9 Решение
Решим уравнение выделением квадрата
двучлена:




РешениеРешим уравнение выделением квадратадвучлена: или

или

х=4 х=1








Слайд 10 Уравнения приводящиеся к квадратным
Биквадратные
Симметричные
Однородные
Возвратные или

Уравнения приводящиеся к квадратнымБиквадратныеСимметричныеОднородные Возвратные или обобщенно-симметрическиеЛогарифмическиеПоказательныеТригонометрические

обобщенно-симметрические
Логарифмические
Показательные
Тригонометрические









Слайд 11






Уравнения приводящиеся к квадратным
1.Биквадратное уравнение

Уравнения приводящиеся к квадратным 1.Биквадратное уравнение сводится к квадратному заменой x² переменной y.

сводится к квадратному заменой x²
переменной y.

Слайд 12 Уравнения приводящиеся к квадратным
3.Уравнение

сводится к квадратному уравнению

Уравнения приводящиеся к квадратным3.Уравнение сводится к квадратному уравнению заменой

заменой

Из уравнений
и

корни имеет только второе :








Слайд 13 Уравнения приводящиеся к квадратным
4.Вообще, замена

Уравнения приводящиеся к квадратным4.Вообще, замена – одна из

– одна из наиболее часто
встречающихся.

Например, с помощью такой замены
к квадратному уравнению (после деления обеих
частей уравнения на ) сводится уравнение вида
.
 Уравнение этого вида обычно называют возвратным
или обобщенно-симметрическим.








Слайд 14 Уравнения приводящиеся к квадратным
6. Уравнение

Уравнения приводящиеся к квадратным 6. Уравнение «симметричное» относительно ,сводится


«симметричное» относительно ,сводится к


биквадратному уравнению заменой y=x+1;
аналогично уравнение ,
«симметричное» относительно x+3, сводится к
биквадратному уравнению заменой y=x+3 .
Отметим ,что для второго уравнения годится и замена
, тогда .








Слайд 15 Основные способы решения уравнений приводящихся к квадратным уравнениям

Основные способы решения уравнений приводящихся к квадратным уравнениям Замена переменной Разложением

Замена переменной
Разложением на множители
Доведением до полного квадрата
С

помощью теоремы Безу
С помощью схемы Горнера

Слайд 16 Решение квадратных уравнений и приводящихся к ним.
x4+ 4

Решение квадратных уравнений и приводящихся к ним. x4+ 4 x2

x2 –21 = 0 – биквадратное уравнение.
Пусть x2=

t ,t ≥ 0, тогда получим уравнениеt2 – 4t-21 = 0.
По обратной теореме Виета t1= – 7, t2= 3.
t = – 7 ― не удовлетворяет условию t ≥ 0, поэтому решим уравнение:
 

 



Слайд 17 Решение квадратных уравнений и приводящихся к ним.

Однородное уравнение

Решение квадратных уравнений и приводящихся к ним. Однородное уравнение относительно

относительно и

.
Разделим обе части уравнения на и получим:

 

Пусть , тогда
Для нахождения x решаем совокупность уравнений:
1)
 


2)
 
 
 

 








Слайд 18 Решение квадратных уравнений и приводящихся к ним.



ОДЗ:

Решение квадратных уравнений и приводящихся к ним. ОДЗ: Пусть

Пусть

, тогда и уравнение примет вид



- не удовлетворяет условию t>0.


откуда
или и
Решая полученные уравнения, находим
 






Слайд 19 Решение квадратных уравнений и приводящихся к ним.
t2 –

Решение квадратных уравнений и приводящихся к ним.t2 – 6t + 1

6t + 1 = 0












Ответ: х = ±2


Слайд 20 Решение квадратных уравнений и приводящихся к ним.












Ответ: х

Решение квадратных уравнений и приводящихся к ним.Ответ: х = 0, 1

= 0, 1




а2 + а – 2 =

0

а = 1

Слайд 21










.
ОДЗ:

≠
Ответ:
Решение квадратных уравнений и приводящихся к ним.

. ОДЗ:≠Ответ:Решение квадратных уравнений и приводящихся к ним.
  • Имя файла: prezentatsiya-po-algebre-na-temu-klassifikatsiya-kvadratnyh-uravneniy-i-uravneniy-privodimyh-k-kvadratnym.pptx
  • Количество просмотров: 79
  • Количество скачиваний: 0
- Предыдущая Презентация к уроку ОДНКНР в 5 классе Моя семья-моё богатство
Следующая - Презентация творческой игры Модный показ

Похожие презентации

Всё о неравенствах Всё о неравенствах 152
ребусы и задачи ребусы и задачи 163
Презентация по алгебре на тему Уравнение прямой вида у = kх + l Презентация по алгебре на тему Уравнение прямой вида у = kх + l 191
Первый урок по алгебре 8 класс Первый урок по алгебре 8 класс 265
Геометрическая прогрессия 9 класс Геометрическая прогрессия 9 класс 193
Исследование математических моделей Исследование математических моделей 156
Теория вероятности. Решение задач. Теория вероятности. Решение задач. 174
Презентация по математике на темуСвоя игра Презентация по математике на темуСвоя игра 175
Дидактическая игра на тему ВПР Анализ диаграмм Дидактическая игра на тему ВПР Анализ диаграмм 174
Презентация к уроку алгебры на тему Графическое представление статистических данных Презентация к уроку алгебры на тему Графическое представление статистических данных 241
Урок по теме Решение линейных неравенств с одной переменной и их систем Урок по теме Решение линейных неравенств с одной переменной и их систем 188
Применение неравенств и их свойств Применение неравенств и их свойств 163
Презентация по алгебре на тему Производная 10 класс Презентация по алгебре на тему Производная 10 класс 79
Сложение и вычитание десятичных дробей Сложение и вычитание десятичных дробей 135
Урок-презентация по теме Неравенство треугольникагеометрия 7 класс Урок-презентация по теме Неравенство треугольникагеометрия 7 класс 233
Степень с целым показателем Степень с целым показателем 126
Тангенс суммы и разности аргументов презентация для 10 класса Тангенс суммы и разности аргументов презентация для 10 класса 208
Презентация по теме: Квадратные уравнения Презентация по теме: Квадратные уравнения 159
Показательная функция, решение уравнений и неравенств Показательная функция, решение уравнений и неравенств 172
Презентация по математике в 6 классе использование пропорций при построении диаграмм Презентация по математике в 6 классе использование пропорций при построении диаграмм 163
Последовательность Последовательность 143
Решение рациональных уравнений Решение рациональных уравнений 170
Подготовка к ГИА. Алгебраические выражения Подготовка к ГИА. Алгебраические выражения 192
Презентация по алгебре Умножение одночлена на многочлен (7 класс) Презентация по алгебре Умножение одночлена на многочлен (7 класс) 166
Презентация по алгебре Решение дробных- рациональных уравнений 8класс Презентация по алгебре Решение дробных- рациональных уравнений 8класс 146
Логарифм числа Логарифм числа 165
Упрощение выражений Упрощение выражений 210
Презентация Степенная функция 9 класс Презентация Степенная функция 9 класс 188
Экзаменационная работа по алгебре, 9 класс (демонстрационный вариант) Экзаменационная работа по алгебре, 9 класс (демонстрационный вариант) 190
Презентация математика 10 класс Презентация математика 10 класс 169