- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение уравнений при подготовке к ОГЭ.
Содержание
- 2. ВопросыОпределение уравнения;Корень уравнения;Что значить решить уравнение?
- 4. Сколько корней может иметь линейное уравнение
- 5. Решите устно:1. 14x=-72. 3x=03. |x|=84. |x|+9=85. 0x=06. 0x=2,37. 8. |x-6|=5 x-6=5 или x-6=-5
- 6. Квадратные уравнения:Неполные квадратные уравнения:x=0 или (ax+b)=0ax2+c=0 ax2+bx+c=0ax2+bx=0x(ax+b)=0x=-b:ax=где ас
- 8. Приведенное квадратное уравнение : x2+px+q=0Теорема Виетаx1+x2=-px1·x2=qФормула разложения
- 9. Решите устно:2x2-32=04x2 +25=0x2 -4x-5=0
- 10. Дробно – рациональные уравнения: Алгоритм решения
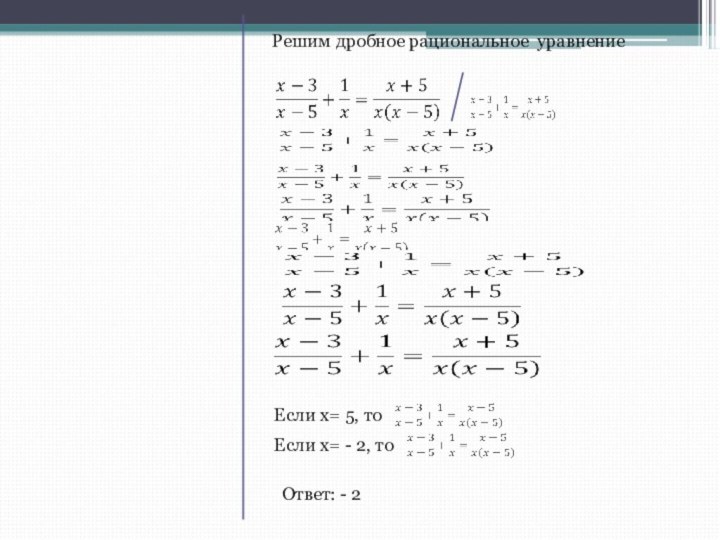
- 11. Решим дробное рациональное уравнение Если x= 5, то Если x= - 2, то Ответ: - 2
- 12. Гимнастика для глазВертикальные движения
- 13. Уравнение вида
- 14. введем новую переменную
- 15. Обратная подстановка дает: Решив их получим:Ответ:
- 16. Кубическое уравнение – алгебраическое уравнение третьей степени.
- 17. Скачать презентацию
- 18. Похожие презентации
ВопросыОпределение уравнения;Корень уравнения;Что значить решить уравнение?
















Слайд 4
Сколько корней может иметь
линейное уравнение ax=-b
?
Линейными называются уравнения
вида аx+b=0
Слайд 5
Решите устно:
1. 14x=-7
2. 3x=0
3. |x|=8
4. |x|+9=8
5. 0x=0
6. 0x=2,3
7.
8. |x-6|=5
x-6=5 или x-6=-5
Слайд 6
Квадратные уравнения:
Неполные квадратные уравнения:
x=0 или (ax+b)=0
ax2+c=0
ax2+bx+c=0
ax2+bx=0
x(ax+b)=0
x=-b:a
x=
где ас
Слайд 7
Дискриминант
Если D>0, то уравнение имеет 2 корня.
Если D=0, то уравнение имеет 1 корень.
(2 равных корня)
Если D<0, то уравнение не имеет корней.
Слайд 8
Приведенное квадратное уравнение :
x2+px+q=0
Теорема Виета
x1+x2=-p
x1·x2=q
Формула разложения квадратного
трёхчлена на множители:
аx2+bx+c=a(x-x1)(x-x2)
где x1, x2 – корни квадратного
трёхчлена
Слайд 10
Дробно – рациональные уравнения:
Алгоритм решения дробно-рационального
уравнения:
1) найти общий знаменатель дробей, входящих в уравнение;
2)
умножить обе части уравнения на общий знаменатель;3) решить получившееся целое уравнение;
4) исключить из его корней те, которые обращают в нуль общий знаменатель.
Слайд 12
Гимнастика для глаз
Вертикальные движения глаз
вверх – вниз.
Горизонтальное – вправо – влево.
Вращение глазами по
часовой стрелке и против.Закрыть глаза и представить по очереди цвета радуги как можно отчетливее.
Слайд 13
Уравнение вида
, где
а, b, c – данные числа и а отлично от нуля, а х –неизвестное, называют биквадратным уравнением.
Чтобы решить биквадратное уравнение, вводят новую переменную у = х2
Тогда исходное уравнение превращается в квадратное относительно неизвестного y.
Слайд 14
введем новую переменную
где у
0исходное уравнение примет вид:
так как то оно имеет
два корня.
Корни находим по теореме Виета
Слайд 16
Кубическое уравнение – алгебраическое уравнение третьей степени.
Общий вид кубического уравнения:
ax³+bx²+cx+d=0,
где a≠0Пример:
х³+2x²-x-2=0
x²(х+2) – (х+2)=0
(х+2)(x²-1)=0
(х+2)(х-1)(х+1)=0
х=-2; х=-1; х=1