Презентация на тему по математике Квадратные уравнения

где х –переменная,

а, в и с

некоторые числа,

причем а 0.

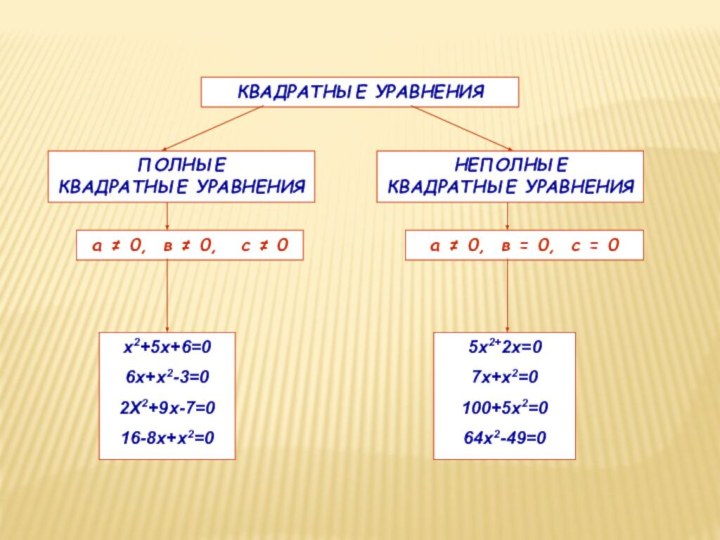
ОПРЕДЕЛЕНИЕ:

Квадратным уравнением называется

0, с ≠ 0
а ≠ 0, в =

0, с = 0

х2+5х+6=0
6х+х2-3=0
2Х2+9х-7=0
16-8х+х2=0

5х2+2х=0
7х+х2=0
100+5х2=0
64х2-49=0

скобки:
х(ах + в) = 0
2.

Разбиение уравнения
на два равносильных:
х=0 и ах + в = 0
3. Два решения:
х = 0 и х = -в/а

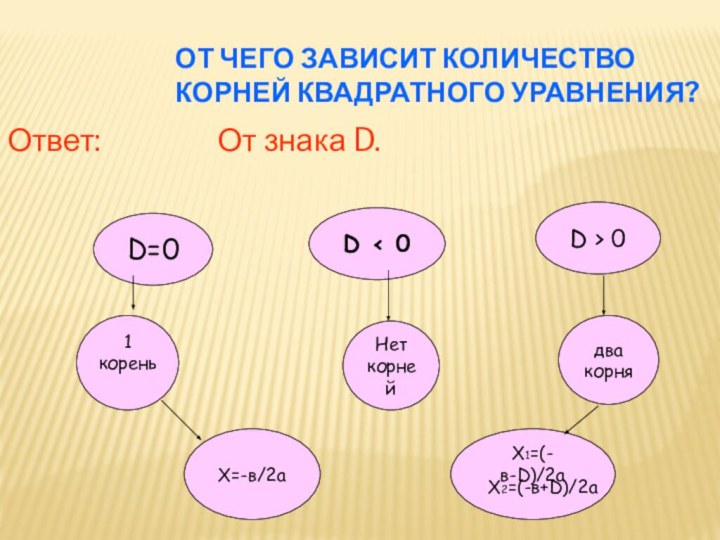
1.Деление обеих частей уравнения на а.
х2 = 0
2.Одно решение: х = 0.

б) ( х + 2)2 + ( х -3)2 = 13

2 вариант:
а) 3х + 2х2= 0
б) 9х2 – 25 = 0

3 вариант:
а) 5х2 – 3х = 0
б) 100 + 5х2 = 0

= b2- 4ac, x1,2=


Теорема Виета.

От знака

D.

Х2=(-в+D)/2а

коэффициенту, взятому с противоположным знаком, а произведение корней равно

свободному члену.
х²+px+g=0- приведенное квадратное уравнение.
П о теореме Виета: х1 + х2= -p
х1* х2= g

математика и астронома Ариабхатты.
Другой индийский ученый Брахмагупта (VII в)

изложил общее правило решения квадратных уравнений, которое практически совпадает с современным.
В Древней Индии были распространены публичные соревнования в решении трудных задач. Задачи часто облекались в стихотворную форму.
________________________________________________
Задача Бхаскары:
Обезьянок резвых стая, всласть поевши, развлекалась.
Их в квадрате часть восьмая на полянке забавлялась.
А двенадцать по лианам стали прыгать, повисая.
Сколько ж было обезьянок, ты скажи мне, в этой стае?

тогда на поляне забавлялось – .
Составим

уравнение:

+ 12 = х

Ответ: х1= 16 , х2= 48 обезьянок.