- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Вычисление площадей плоских фигур
Содержание
- 2. Цель занятияЗакрепить умения применять определённый интеграл при вычислении площадей плоских фигур
- 3. Символ введен Г. Лейбницем в 1675 г.
- 4. Смысл там, где змеи интегралаМеж цифр и
- 5. Что такое бионика?Лозунг бионики «Природа знает лучше»
- 6. Знаем:
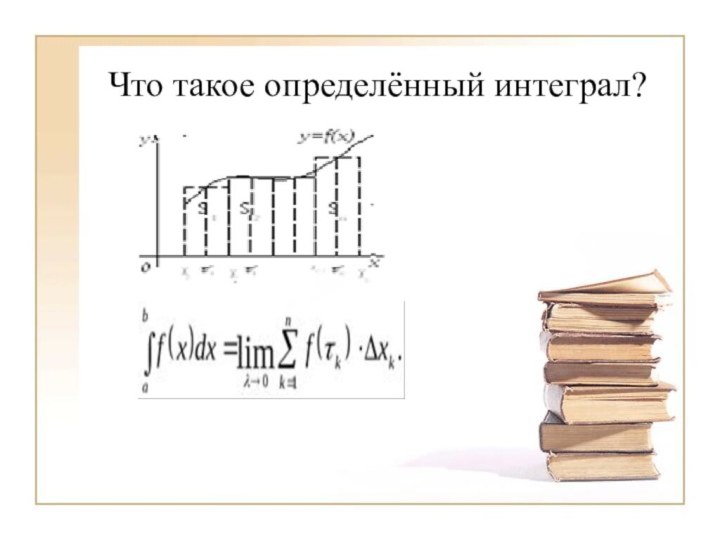
- 7. Что такое определённый интеграл?
- 8. Свойства определённого интеграла
- 9. Самостоятельная работа
- 10. ответыКритерии отметки : «3» - 4 правильных
- 11. Знаем:1.Как вычислить интеграл2. Что такое криволинейная трапеция3.
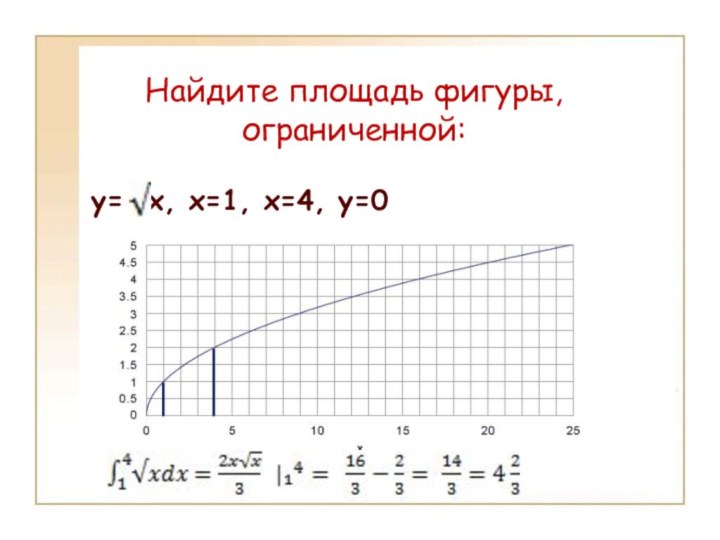
- 13. Найдите площадь фигуры, ограниченной:y= x, x=1, x=4, y=0
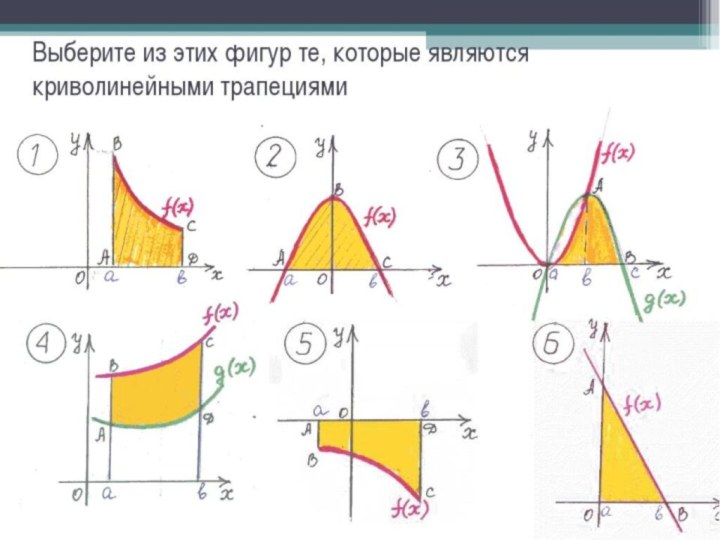
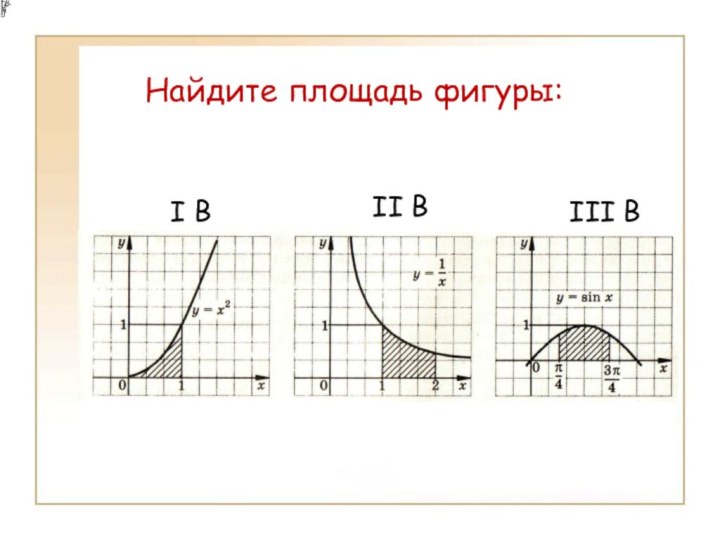
- 14. Найдите площадь фигуры:I BIII BII B
- 15. Задача 4.
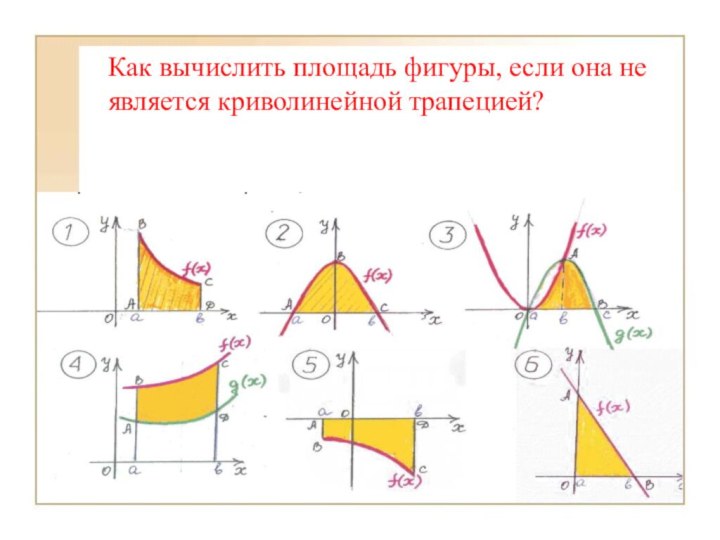
- 16. Как вычислить площадь фигуры, если она не является криволинейной трапецией?
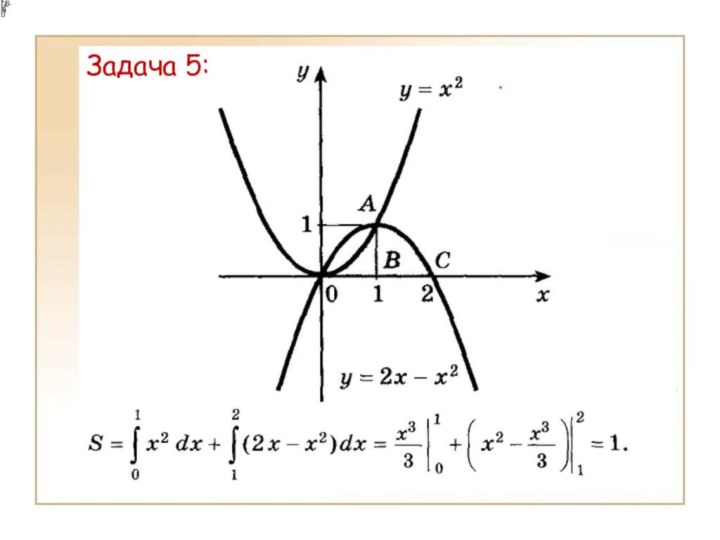
- 17. Задача 5:
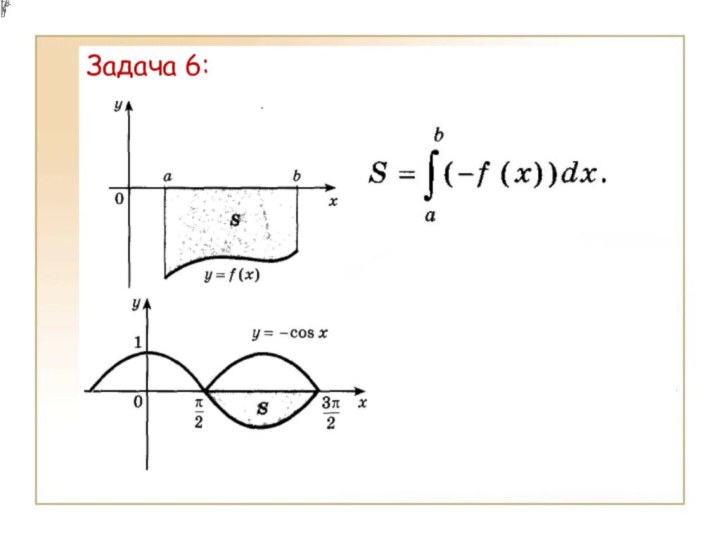
- 18. Задача 6:
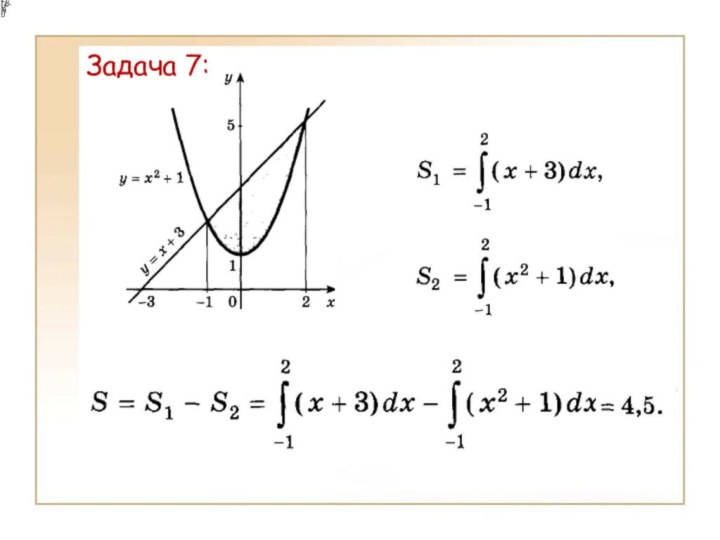
- 19. Задача 7:
- 20. Домашнее задание:Вариант 35,36 стр.215Составить свою задачу на нахождение площади плоской фигуры и решить её.
- 21. Скачать презентацию
- 22. Похожие презентации
Цель занятияЗакрепить умения применять определённый интеграл при вычислении площадей плоских фигур












Слайд 2
Цель занятия
Закрепить умения применять определённый интеграл при вычислении
площадей плоских фигур
Слайд 3 Символ введен Г. Лейбницем в 1675 г. Этот
знак является изменением латинской буквы «S» (первой буквы слова «сумма»).
Само слово «интеграл» придумал в 1690 г. Я. Бернулли. Вероятно, оно происходит от латинского «integero», которое переводится как «приводить в прежнее состояние, восстанавливать». Действительно, операция интегрирования «восстанавливает» функцию, дифференцированием которой была получена подынтегральная функция. В ходе переписки И. Бернулли и Г. Лейбниц согласились с предложением Я. Бернулли , и с 1696 г. появилось название новой ветви математики –«интегральное исчисление». Понятие «неопределенный интеграл» выделил Г. Лейбниц, а «определенный интеграл» ввел К. Фурье. Связь операций дифференцирования и интегрирования независимо друг от друга установили И. Ньютон и Г. Лейбниц»Г.Лейбниц
И.Ньютон
Слайд 4
Смысл там, где змеи интеграла
Меж цифр и букв,
меж d и f.
Там - власть, там творческие горны!
Пред
волей чисел все – рабы.И солнца путь вершат, покорны
Немым речам и ворожбы.
В. Брюсов
В.Брюсов
Слайд 10
ответы
Критерии отметки :
«3» - 4 правильных ответа
«4» - 5 правильных ответов
«5» - 6 правильных ответов
Слайд 11
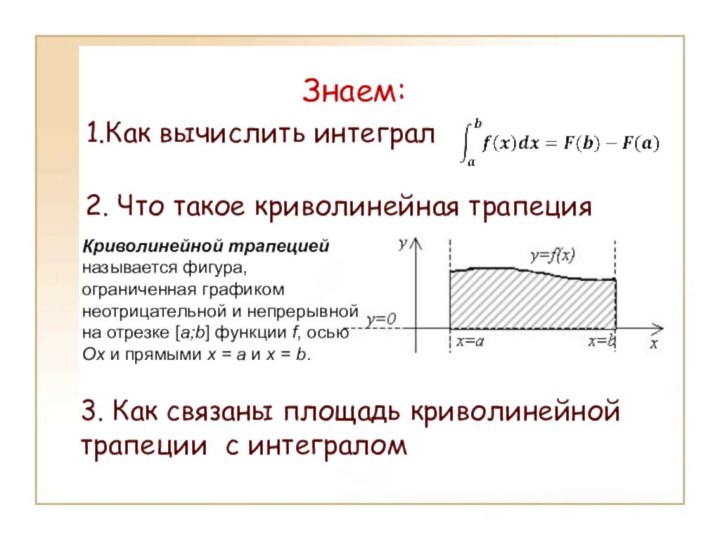
Знаем:
1.Как вычислить интеграл
2. Что такое криволинейная трапеция
3. Как
связаны площадь криволинейной
трапеции с интегралом
Криволинейной трапецией называется фигура,
ограниченная графиком неотрицательной и непрерывной на отрезке [a;b] функции f, осью Ox и прямыми x = a и x = b.





























