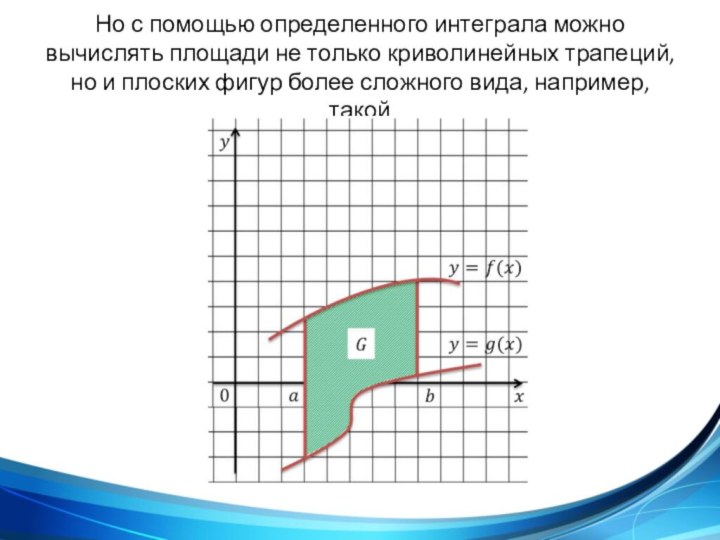
не только криволинейных трапеций, но и плоских фигур более
сложного вида, например, такойтакой
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть



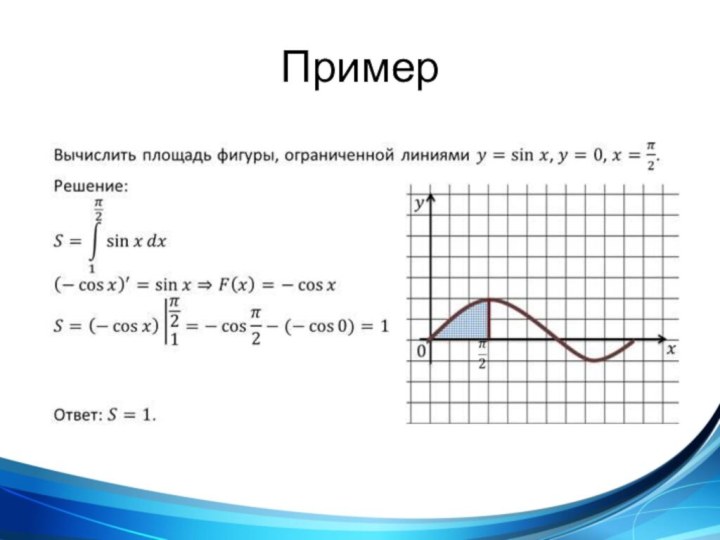
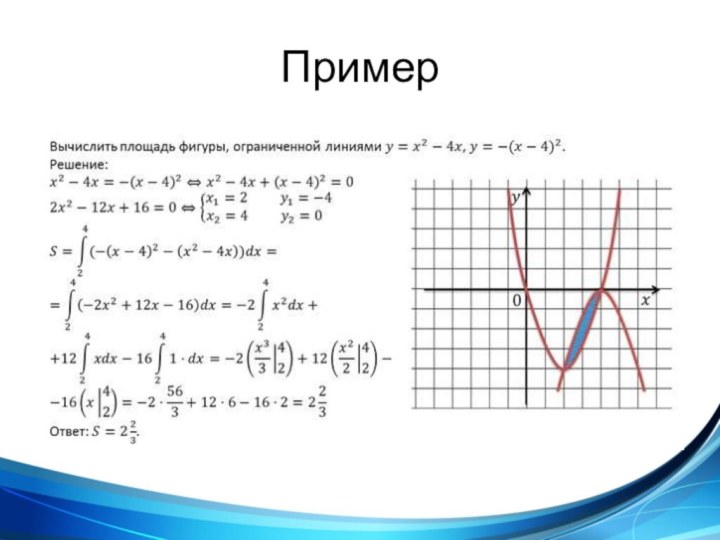
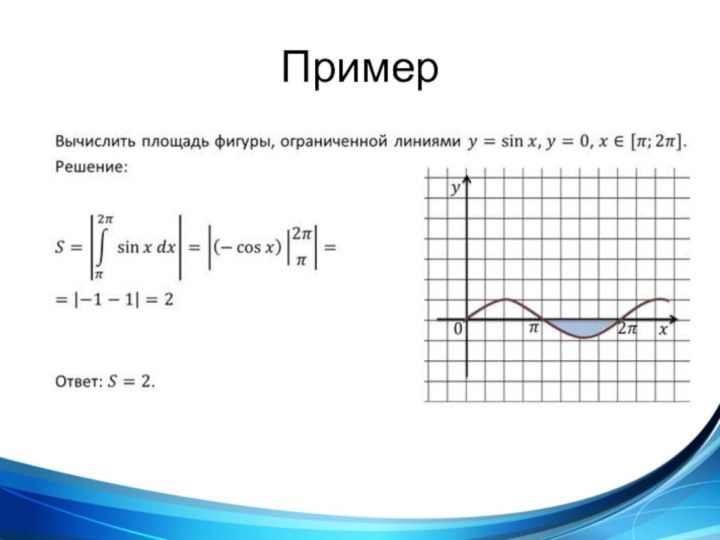
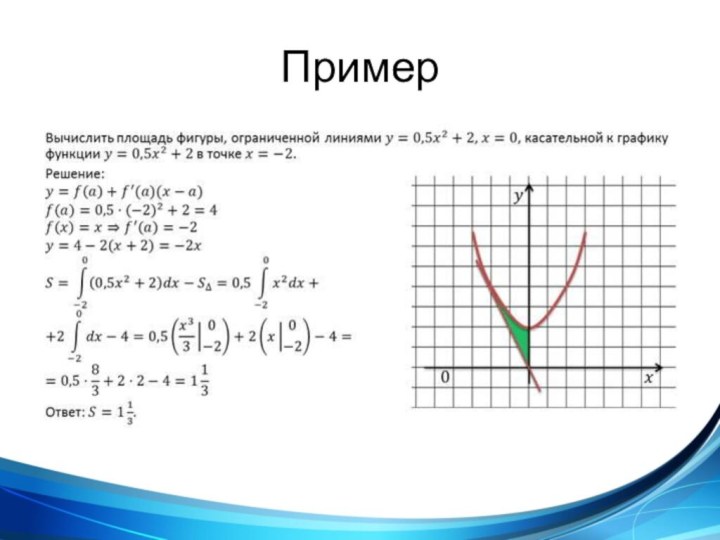
такой