Слайд 2
Цели проекта:
1. Расширить кругозор учащихся, способствовать развитию
познавательного интереса.
2. Показать школьникам общеинтеллектуальное значение математики.
3. Способствовать познанию
законов красоты и гармонии окружающего мира.
Задачи:
1. Ввести понятие «золотого сечения», «золотого треугольника», «золотого прямоугольника».
2. Определить числовое значение золотого отношения.
3. Показать деление отрезка в золотом отношении.
4. Рассказать, где встречается золотое сечение в природе, живописи,
архитектуре, показать связь золотого отношения и тела человека.
Методы исследования:
анализ литературы, сопоставление фактов, психологические опыты.
Форма проекта: индивидуальная.
Тип проекта: информационно-творческий.
Предметно-содержательная область: межпредметный.
Область исследования: математика, живопись, биология, история.
Слайд 3
Эпиграф:
«…Геометрия владеет двумя сокровищами – теоремой Пифагора и
золотым сечением, и если первое из них можно сравнить
с мерой золота, то второе – с драгоценным камнем…»
Иоганн Кеплер
Слайд 4
Золотое сечение в математике
В математике пропорцией называют равенство
двух отношений: a : b = c : d
Отрезок
прямой АВ можно разделить на две части следующими способами:
-на две равные части – АВ :АС=АВ:ВС;
-на две неравные части в любом отношении;
-таким образом, когда АВ:АС = АС:ВС.
Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.
Слайд 5
Определение:
Золотое сечение – это такое пропорциональное деление отрезка
на неравные части, при котором весь отрезок так относится
к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему
a : b = b : c или c : b = b : a
Слайд 6
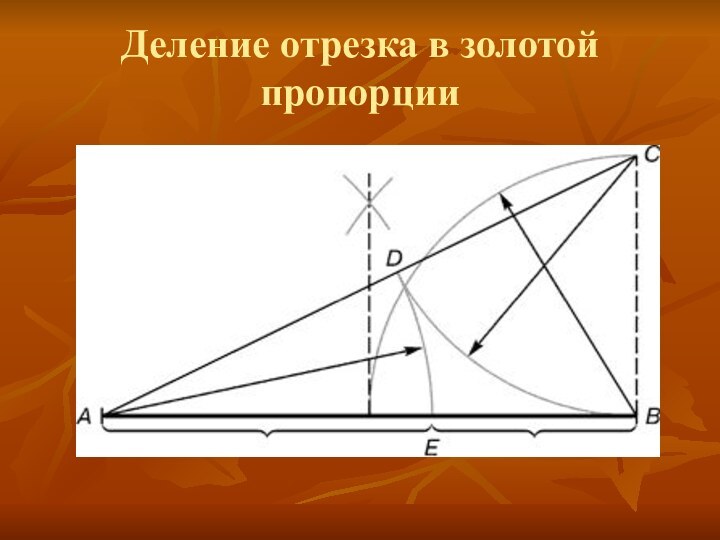
Деление отрезка в золотой пропорции
Слайд 7
Числовое значение золотого отношения
Обозначим ВЕ =х, тогда АХ
= 1-х (так как АВ примем за 1) и
по условию задачи
(1 –х) : х = х : 1.
Отсюда х2 = 1 – х или х2 + х – 1 = 0.
Решения этого уравнения:
х = 1,61803398875 или х = -1,618033...
Из двух значений корня выбираем первое, так как другое значение оказалось отрицательным.
Полученное число обозначается буквой φ.
Слайд 8
Примеры золотого сечения в математике
ПЕНТАГРАММА- правильный невыпуклый пятиугольник
Человеческое
тело можно рассматривать как пятилучевую фигуру, где лучами служат
голова, руки и ноги.
Слайд 9
Числа Фибоначчи
Последовательность чисел Фибоначчи: каждое число в этой
последовательности получается из суммы двух предыдущих чисел.
0,1,1,2,3,5,8,13,21,34,55,89,144,233,…
При делении любого
числа из последовательности на число, стоящее перед ним в ряду, результатом всегда будет величина 1,618033..
Слайд 10
Золотой треугольник
Золотым называется такой равнобедренный треугольник, основание и
боковая сторона которого находятся в золотом отношении
Слайд 11
Золотой прямоугольник
Примером золотого сечения в математике является прямоугольник,
стороны которого находятся в золотом отношении, т.е. отношение ширины
к длине дает число φ.
Этот прямоугольник обладает необычными свойствами: отрезав от него квадрат, сторона которого равна меньшей стороне прямоугольника, снова получим золотой прямоугольник. Этот процесс можно продолжать до бесконечности. Причем располагаться прямоугольники будут по логарифмической спирали,
Слайд 13
Золотое сечение в живописи
Портрет «Мона Лиза» Леонардо да
Винчи написан в соответствии с золотой пропорцией
Картина «Тайная вечеря»
может
быть представлена в виде
золотого прямоугольника.
Слайд 14
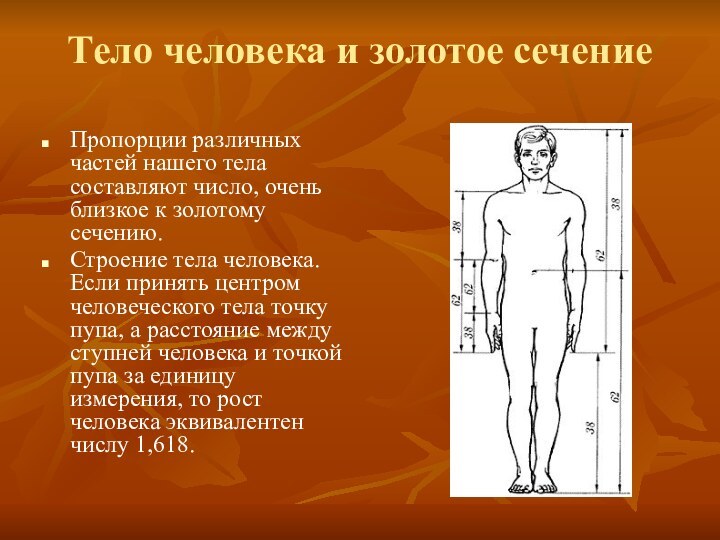
Тело человека и золотое сечение
Пропорции различных частей нашего
тела составляют число, очень близкое к золотому сечению.
Строение тела
человека. Если принять центром человеческого тела точку пупа, а расстояние между ступней человека и точкой пупа за единицу измерения, то рост человека эквивалентен числу 1,618.
Слайд 16
Черты лица
В строении черт лица человека также есть
множество примеров, приближающихся по значению к формуле золотого сечения.