- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математикеРешение задач и пути ее реализацииЗадачи на смеси и сплавы 10-11 класс
Содержание
- 2. Задача: Сколько кг воды нужно выпарить
- 3. Решение задачи:1) 100% - 90% =10%, что
- 4. Понятия:Абсолютное содержание вещества в смеси – это
- 5. Иллюстрация понятия: Предположим, что в
- 6. а) Смешали две смеси. При образовании
- 7. Пример 1:Смешали 500г 10% раствора соли и
- 8. Абсолютное содержание соли:в I растворе 500٠0,1
- 9. Общий подход к данному типу задач:
- 10. б) Отлили часть раствора (отрезали кусок сплава).Пример2:
- 11. Пример2: От куска сплава золота с серебром
- 12. Пример3: Руда содержит 40% примесей, а
- 13. Пример3: Руда содержит 40% примесей, а
- 14. Пример 4: В двух литрах водного раствора,
- 15. Пример 4: В двух литрах водного раствора,
- 16. Пример 5: Сколько литров воды нужно добавить
- 17. Пример 5: Сколько литров воды нужно добавить
- 18. Пример 6: Сколько л. воды нужно выпарить
- 19. Пример 6: Сколько л. воды нужно
- 20. Пример 7: Сплав состоящий из двух металлов
- 21. Система уравнений:Ответ: 10 кг,8кг.Пример 7: Сплав состоящий
- 22. Пример 8: Имеется лом стали двух сортов
- 23. Система уравнений:Ответ: 40тонн, 100 тонн.Пример 8: Имеется
- 24. в) Задачи на многократные переливания.Пример 1:
- 25. Пример 1: В ведре
- 26. Пример 2: В ведре находится 10
- 27. Пример 2: В ведре находится 10
- 28. Пример 3: В двух одинаковых сосудах объемом
- 29. Пример 3: В двух одинаковых сосудах объемом
- 30. Г) Более сложные задачи: Пример 1: Имеется
- 31. 250 ▪ 0,3 = 75(кг) цинка 2
- 32. Пример 2: Из 2 растворов с различным
- 33. Пример 2: Из 2
- 34. Пример 1: Арифметический старинный способ В каких
- 35. Алгебраический способ х - количество 50% кислотыу - количество 70% кислоты(х+у) - количество смесиОтвет: 1:3
- 36. Алгоритм решения задач на смеси и сплавы:1.
- 37. Тестовые задания
- 38. Скачать презентацию
- 39. Похожие презентации



































Слайд 3
Решение задачи:
1) 100% - 90% =10%, что составляет
10 кг «чистого вещества».
2) Выпарили х кг, осталось
(100 – х) кг,20% =
Уравнение:
50=100 – х
Х =50 Ответ: 50кг.
Слайд 4
Понятия:
Абсолютное содержание вещества в смеси – это количество
вещества, выраженное в обычных единицах измерения (грамм, литр и
т. д.).Относительное содержание вещества – это отношение абсолютного содержания вещества к общей массе (объему) смеси.
Часто относительное содержание вещества называют концентрацией или процентным содержанием, при этом используют различные записи относительного содержания вещества: в долях, процентах.
Слайд 5 Иллюстрация понятия: Предположим, что в сосуд, содержащий 450
г воды, добавили 50 г соли. Общая масса полученного
раствора 500гАбсолютное содержание соли 50г, относительное содержание соли
Абсолютное содержание воды 450г, относительное содержание воды .
50 г 1
500 г 10
=
=
10 %
450 г 9
500 г 10
=
= 0,9 = 90 %
450 г 9
Слайд 6
а) Смешали две смеси.
При образовании смеси
складываются абсолютные содержания. Поэтому, если известны только относительные содержания,
то нужно:1. Подсчитать абсолютные содержания;
2. Сложить абсолютные содержания, компонент.
3. Подсчитать относительные содержания компонента.
Слайд 7 Пример 1:Смешали 500г 10% раствора соли и 400г
55% раствора соли. Определите концентрацию
соли в смеси.
Слайд 8
Абсолютное содержание соли:
в I растворе 500٠0,1 =
50г.
во II растворе 400٠0,55 = 220г.
Смесь двух исходных
растворов составляет: Соль 10%
Вода 90%
500 г
Соль 55%
Вода 45%
400 г
Соль %
Вода %
Решение:
Слайд 9
Общий подход к данному типу задач:
- масса соли в I
растворе- масса соли во II растворе
- масса соли при смешивании
Процентное содержание соли в смеси:
Р1m1
100
P2m2
100
P1m1+p2m2
100
P1m1 + p2m2
100
٠100
m1 + m2
P =
p1m1 + p2m2
=
m1 + m2
p1m1 + p2m2 = p (m1 + m2)
Слайд 10
б) Отлили часть раствора (отрезали кусок сплава).
Пример2: От
куска сплава золота с серебром массой 500 г и
10% содержанием золота отрезали 20 г. Определите количество золота и серебра в отрезанном куске.Слайд 11 Пример2: От куска сплава золота с серебром массой
500 г и 10% содержанием золота отрезали 20 г.
Определите количество золота и серебра в отрезанном куске.Золото 10 %
Серебро 90 %
Золото 10 %
Серебро 90 %
отрезали
500г
20 г
1) 20 ٠0,1 = 2 г 2) 20 ٠ 0,9 = 18 г
Слайд 12 Пример3: Руда содержит 40% примесей, а выплавленный
металл 4% примесей. Сколько получится металла из 24 т
руды?Слайд 13 Пример3: Руда содержит 40% примесей, а выплавленный
металл 4% примесей. Сколько получится металла из 24 т
руды?
Чистый металл 60%
Примеси 40%
Руда 24 т
Чистый металл 96%
Примеси 4%
Металл х т
Процесс плавки
24 ٠ 0,4 = 9,6 т
24 – 9,6 = 14,4 т
Х – 0,04 х = 0,96 х
0,96 х = 14,4
Х = 15
Слайд 14 Пример 4: В двух литрах водного раствора, содержащего
60% кислоты добавили 4 литра чистой воды. Определить %
содержание кислоты в новом растворе?Слайд 15 Пример 4: В двух литрах водного раствора, содержащего
60% кислоты добавили 4 литра чистой воды. Определить %
содержание кислоты в новом растворе? Ответ можно получить по рассмотренной ранее формуле:
P =
P1V1 + P2V2 60 ٠ 2 + 0 ٠ 4 60 ٠ 2
V1 + V2 2 + 4 6
=
=
= 20%
Слайд 16 Пример 5: Сколько литров воды нужно добавить в
2 литра водного раствора, содержащего 60 % кислоты, чтобы
получить 20 % раствора кислоты?Слайд 17 Пример 5: Сколько литров воды нужно добавить в
2 литра водного раствора, содержащего 60 % кислоты, чтобы
получить 20 % раствора кислоты?
Арифметический способ:
2 ٠3 = 6 л.
6л – 2л = 4л
Алгебраический способ:
0,6 ٠ 2 = 0,2 (х + 2)
Х = 4
Слайд 18 Пример 6: Сколько л. воды нужно выпарить из
20л раствора, содержащего 80% воды, чтобы получить раствор, содержащий
75% воды?Слайд 19 Пример 6: Сколько л. воды нужно выпарить из
20л раствора, содержащего 80% воды, чтобы получить раствор, содержащий
75% воды?
Примеси в водном растворе
100% - 80% = 20%
Стало:
100% - 75% = 25%
Примеси увеличилось в
25 : 20 = 1,25 раза
20 : 1,25 = 16л
20 – 16 = 4л
Объем уменьшить в 1,25 раза
Слайд 20 Пример 7: Сплав состоящий из двух металлов весит
18 кг. После того как из него выделили 40%
первого и 25% второго, в нем первого металла осталось столько же, сколько второго. Сколько килограмм каждого металла было первоначально в сплаве?
Слайд 21
Система уравнений:
Ответ: 10 кг,8кг.
Пример 7: Сплав состоящий из
двух металлов весит 18 кг. После того как из
него выделили 40% первого и 25% второго, в нем первого металла осталось столько же, сколько второго. Сколько килограмм каждого металла было первоначально в сплаве?Слайд 22 Пример 8: Имеется лом стали двух сортов с
содержанием никеля 5% и 40%. Сколько нужно взять каждого
из этих сортов, чтобы получить 140 тонн стали с содержанием никеля 30%.
Слайд 23
Система уравнений:
Ответ: 40тонн, 100 тонн.
Пример 8: Имеется лом
стали двух сортов с содержанием никеля 5% и 40%.
Сколько нужно взять каждого из этих сортов, чтобы получить 140 тонн стали с содержанием никеля 30%.
Слайд 24
в) Задачи на многократные переливания.
Пример 1:
В ведре находится 10 литров чистого, а в
баке 20 литров 40 % раствора этого спирта. Некоторое количество спирта из ведра перелили в бак, полученную смесь перемешали и точно такое же количество перелили обратно. Эту операцию повторили несколько раз, соблюдая следующие условия: в ведро переливают такое же количество раствора, какое перед этим перелили в бак; после каждого переливания раствор тщательно перемешивают. После нескольких описанных операций в ведре оказался 70 % раствор спирта. Определите % концентрацию раствора спирта в баке.
Слайд 25
Пример 1:
В ведре находится
10 литров чистого, а в баке 20 литров 40
% раствора этого спирта. Некоторое количество спирта из ведра перелили в бак, полученную смесь перемешали и точно такое же количество перелили обратно. Эту операцию повторили несколько раз, соблюдая следующие условия: в ведро переливают такое же количество раствора, какое перед этим перелили в бак; после каждого переливания раствор тщательно перемешивают. После нескольких описанных операций в ведре оказался 70 % раствор спирта. Определите % концентрацию раствора спирта в баке.Самое важное в задаче заключается в следующем: общее количество спирта в ведре и баке после всех переливаний не изменилось.
Первоначально спирта было 10 + 8 = 18 л. спирта.
В конце процесса в ведре
10 + 8 = 18
10 ▪ 0,7 = 7 л
18 – 7 = 11 л
11 ▪ 100
20
%
=
55%
Слайд 26 Пример 2: В ведре находится 10 л чистого
спирта, а в баке 20 л 75 % раствора
спирта. Некоторое количество спирта переливают в бак, точно такое же количество смеси переливают обратно. В результате в ведре оказался 90 % раствор спирта. Сколько л спирта перелили из ведра в бак?Слайд 27 Пример 2: В ведре находится 10 л чистого
спирта, а в баке 20 л 75 % раствора
спирта. Некоторое количество спирта переливают в бак, точно такое же количество смеси переливают обратно. В результате в ведре оказался 90 % раствор спирта. Сколько л спирта перелили из ведра в бак?В баке
0,75 ٠ 20 = 15 л
спирта, а вместе
10 + 15 = 25 л.
После двух переливаний в ведре
0,9 ٠ 10 = 9 л
спирта
Доля спирта в баке
16
20
=
0,8
После двух переливаний
0,8 х л спирта
.
В баке осталось
15 + х – 0,8х = 15 + 0,2х
А в баке
25 – 9 = 16 л спирта
х – количество переливаемого раствора
Перелитый в ведро раствор содержит 0,8 х л спирта
15 + 0,2 х = 16
Х = 5
Слайд 28 Пример 3: В двух одинаковых сосудах объемом по
30 л каждый, содержится всего 30 л спирта. Первый
сосуд доливают доверху водой и полученной смесью дополняют второй сосуд, затем из второго сосуда отливают в первый 12 л новой смеси. Сколько л. Спирта было первоначально в первом сосуде, если во втором сосуде оказалось на 2 л спирта меньше, чем в первом.Слайд 29 Пример 3: В двух одинаковых сосудах объемом по
30 л каждый, содержится всего 30 л спирта. Первый
сосуд доливают доверху водой и полученной смесью дополняют второй сосуд, затем из второго сосуда отливают в первый 12 л новой смеси. Сколько л. Спирта было первоначально в первом сосуде, если во втором сосуде оказалось на 2 л спирта меньше, чем в первом.В 1 сосуде оказалось 16 л, а во 2 – 14 л спирта.
Пусть было первоначально в 1 сосуде х л, а во 2 (30 – х) л спирта.
После доливания водой первого
сосуда спирт составляет всего объема.
Х
30
Х ▪
Х
30
=
х2
30
Л.,
Стало:
30 – х +
х2
30
л.
Доля спирта
30 – х +
х2
30
30
В 12 л смеси:
12
▪
30 – х +
х2
30
30
12 -
=
2х
5
+
х2
75
. Во 2 сосуде осталось:
или 14 л спирта.
18 -
3х х2
5 50
+
= 14
Ответ: Х1 = 10
Х2 = 20
Во второй сосуд перелили
Слайд 30
Г) Более сложные задачи:
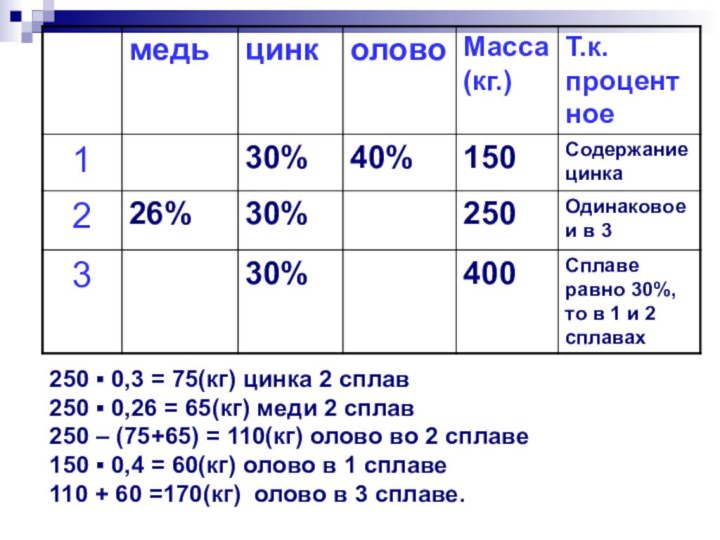
Пример 1: Имеется 2
сплава, состоящие из меди, цинка и олова. Известно, что
1 сплав содержит 40 % олова, а второй 26 % меди. % содержание цинка в 1 и 2 сплаве одинаковое. Сплавив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалось 30 % цинка. Определите, сколько кг олова содержится в получившемся новом сплаве?Слайд 31 250 ▪ 0,3 = 75(кг) цинка 2 сплав
250 ▪ 0,26 = 65(кг) меди 2 сплав
250 –
(75+65) = 110(кг) олово во 2 сплаве150 ▪ 0,4 = 60(кг) олово в 1 сплаве
110 + 60 =170(кг) олово в 3 сплаве.
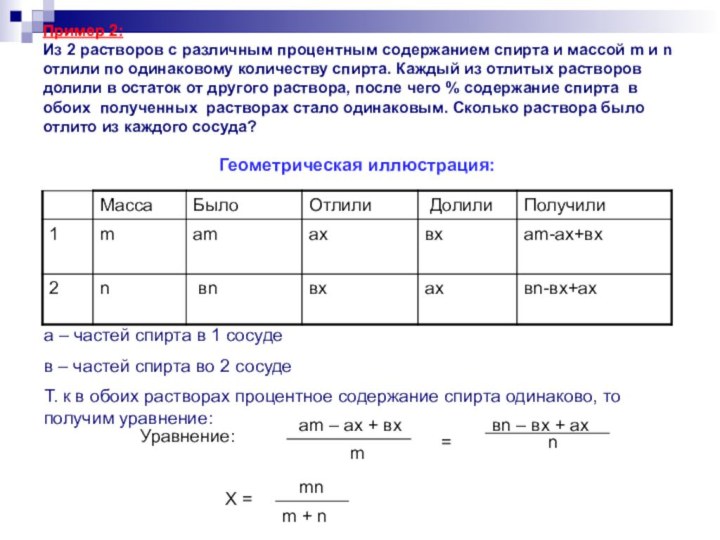
Слайд 32 Пример 2: Из 2 растворов с различным процентным
содержанием спирта и массой m и n отлили по
одинаковому количеству спирта. Каждый из отлитых растворов долили в остаток от другого раствора, после чего % содержание спирта в обоих полученных растворах стало одинаковым. Сколько раствора было отлито из каждого сосуда?Слайд 33 Пример 2: Из 2 растворов с различным процентным
содержанием спирта и массой m и n отлили по
одинаковому количеству спирта. Каждый из отлитых растворов долили в остаток от другого раствора, после чего % содержание спирта в обоих полученных растворах стало одинаковым. Сколько раствора было отлито из каждого сосуда?Уравнение:
am – ax + вx
m
=
вn – вx + ax
n
Х =
mn
m + n
Геометрическая иллюстрация:
а – частей спирта в 1 сосуде
в – частей спирта во 2 сосуде
Т. к в обоих растворах процентное содержание спирта одинаково, то получим уравнение:
Слайд 34
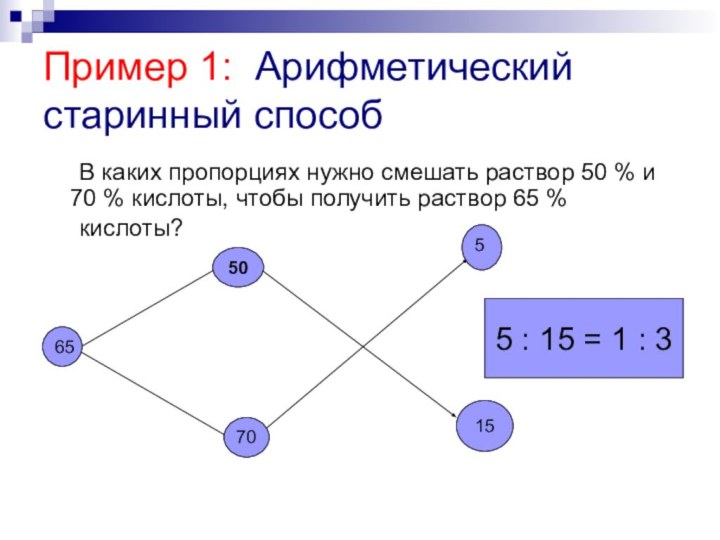
Пример 1: Арифметический старинный способ
В каких пропорциях
нужно смешать раствор 50 % и 70 % кислоты,
чтобы получить раствор 65 %кислоты?
50
70
65
5
15
5 : 15 = 1 : 3
Слайд 35
Алгебраический способ
х - количество 50% кислоты
у -
количество 70% кислоты
(х+у) - количество смеси
Ответ: 1:3
Слайд 36
Алгоритм решения задач на смеси и сплавы:
1. Выбор
неизвестных.
2. Выбор чистого вещества.
3. Переход к долям.
4. Отслеживание состояния
смеси или сплава.5. Составление уравнения или выполнение действий.
6. Формирование ответа.