Презентация на тему по математике на тему Комбинаторные задачи

возможно ли составить комбинацию определённого вида и сколько различных комбинаций можно

 
Пример:
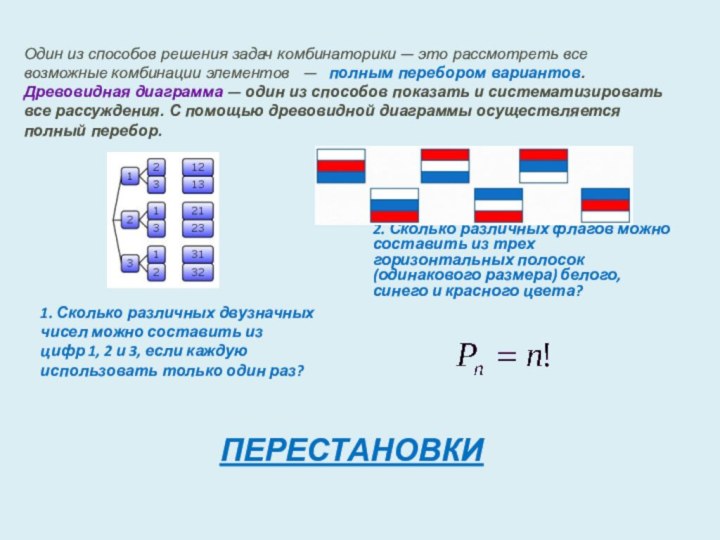
1. Сколько различных двузначных чисел можно составить из цифр 1, 2 и 3, если каждую использовать только один раз?

2. Сколько различных флагов можно составить из трех горизонтальных полосок (одинакового размера) белого, синего и красного цвета?

3. Сколькими различными способами можно составить танцевальную пару, если в коллективе 3 мальчика и 4 девочки?
 
4. Сколькими различными способами можно образовать пару дежурных, если в классе остались Надя, Вика, Саша и Юра?
 
5. Сколькими различными способами можно выбрать двух учеников (одного - мыть доску, второго - подметать пол), если в классе остались Надя, Вика, Саша и Юра? 

цифр 1, 2 и 3, если каждую использовать только один раз?
2. Сколько различных

ПЕРЕСТАНОВКИ

Один из способов решения задач комбинаторики — это рассмотреть все возможные комбинации элементов —  полным перебором вариантов.
Древовидная диаграмма — один из способов показать и систематизировать все рассуждения. С помощью древовидной диаграммы осуществляется полный перебор.

если в классе остались Надя, Вика, Саша и Юра?

№ 4
 

5. Сколькими различными способами можно выбрать двух учеников (одного - мыть доску, второго - подметать пол), если в классе остались Надя, Вика, Саша и Юра?  (Ответ: 12)

№ 5 Используется та же древовидная диаграмма, но в данном случае ответ будет 12 пар, т.к. каждая пара из диаграммы отличается. Если детей поменять местами, они выполняют уже другие функции.
С помощью древовидной диаграммы были получены различные результаты, т.к. в 4 и 5 примере были рассмотрены различные виды комбинаций: сочетания и размещения.
С
А

Будем переставлять их всеми

Будем выбирать из n различных объектов m объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок).
Получившиеся
комбинации
называются 
размещениями 
из n 
объектов
по m

Будем выбирать из n различных объектов  
m объектов всеми возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями 
из n объектов по m

найти число всех возможных исходов независимого проведения двух испытаний А и В,

различными способами это можно сделать?

Решение: На этот раз

кассира. Сколькими различными способами это можно сделать?
Решение: Из 25 человек

Обратите внимание!
Количество сочетаний меньше количества размещений.