- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему 11 класс Логарифм
Содержание
- 2. Цель урока:Дать определение логарифма и основного логарифмического
- 3. Задача 1Найдите положительный корень уравнениях2 = 9х3
- 4. Задача 2Решите уравнение 2х=83х=275х =25ответ: х=3ответ: х=3ответ: х=2
- 5. Определение логарифма Логарифмом положительного числа b по основанию
- 6. Основное логарифмическое тождествоДействие нахождения логарифма числа называется логарифмированием
- 7. Вычислитеloq3 27=loq5 125=loq2 2=loq8 1=loq216=loq3 9=3 loq3 18=loq0,5 0,25=loq2 х= 37 loq7 3=
- 8. Вычислите loq4 1=loq13 13=loq3 х=26loq6 12=loq4х=2loq2 х=5loq13 13=loq3 х=25loq5 12=loq91=
- 9. Вычислите самостоятельно loq3 3=loq2 16=loq2 х=33loq3 18=loq22=loq2 64=loq15 15=loq3 х=24loq4 12=loq91=
- 10. Логари́фм - от греч. λόγος — «слово»,
- 11. Логарифмическая разминка «Немного истории». Параллельно
- 12. Логарифмическая разминка «Немного истории».
- 13. Логарифмическая линейка 1622 год - Первый вариант линейки разработал английский математик-любитель Уильям Отред
- 14. 1630 год -Ричард Деламейн создаёт круговую логарифмическую линейку.
- 15. Англичанин Роберт Биссакар (и независимо от него
- 16. Однако в начале XXI века логарифмические линейки
- 17. Логарифмическая спираль «Удивительное рядом»Спираль – это
- 18. Логарифмическая спираль «Удивительное рядом» Архимедова спиральГиперболическая спираль
- 19. Логарифмическая спираль «Удивительное рядом»
- 20. Логарифмическая спираль «Удивительное рядом»Первым ученым, открывшим
- 21. Логарифмическая спираль «Удивительное рядом»По логарифмическим спиралям выстраиваются цветки в соцветиях подсолнечника
- 22. Логарифмическая спираль «Удивительное рядом»По логарифмическим спиралям выстраиваются рога многих животных
- 23. Живые существа обычно растут, сохраняя общее очертание
- 24. Логарифмическая спираль «Удивительное рядом»По логарифмической спирали свёрнуты раковины многих улиток и моллюсков.
- 26. Логарифмическая спираль «Удивительное рядом»По логарифмической спирали формируется тело циклона
- 27. Логарифмическая спираль «Удивительное рядом»Даже пауки, сплетая паутину, закручивают нити вокруг центра по логарифмической спирали.
- 28. Логарифмическая спираль «Удивительное рядом»
- 29. Логарифмическая спираль «Удивительное рядом»Траектории насекомых
- 30. Логарифмическая спираль «Удивительное рядом»
- 31. И эту спираль мы повсюду встречаем: к
- 32. Очертания, выраженные логарифмической спиралью, имеют не только
- 33. Испуганное стадо северных оленей разбегается по спирали.
- 34. Спиралью закручиваются ураганы и смерчи
- 35. Молекула ДНК закручена двойной спиралью.
- 36. «Логарифмы в музыке» Музыканты редко увлекаются математикой; большинство
- 37. Звезды, шум и логарифмы Этот заголовок связывает столь,
- 39. Любимая цифраВозьмите, пожалуйста, ручки и запишите свою
- 40. Определение логарифма Логарифмом числа b>0 по основанию а>0
- 41. Спасибо за урок!!!
- 42. Скачать презентацию
- 43. Похожие презентации
Цель урока:Дать определение логарифма и основного логарифмического тождестваПоказать полезность применения логарифмов;Научить видеть знакомое в незнакомом, развить интерес к истории математики и её приложениям.








































Слайд 2
Цель урока:
Дать определение логарифма и основного логарифмического тождества
Показать
полезность применения логарифмов;
к истории математики и её приложениям.
Слайд 3
Задача 1
Найдите положительный корень уравнения
х2 = 9
х3 =
8
х4 =
81ответ : х=3
ответ : х=3
ответ : х=2
Слайд 5
Определение логарифма
Логарифмом положительного числа b по основанию а>0
и а 1 называется показатель степени, в
которую нужно возвести число а, чтобы получить число b.Логарифм с произвольным основанием.
Слайд 6
Основное
логарифмическое тождество
Действие нахождения логарифма числа называется логарифмированием
Слайд 7
Вычислите
loq3 27=
loq5 125=
loq2 2=
loq8 1=
loq216=
loq3 9=
3 loq3 18=
loq0,5
0,25=
loq2 х= 3
7 loq7 3=
Слайд 9
Вычислите самостоятельно
loq3 3=
loq2 16=
loq2 х=3
3loq3 18=
loq22=
loq2 64=
loq15
15=
loq3 х=2
4loq4 12=
loq91=
Слайд 10 Логари́фм - от греч. λόγος — «слово», «отношение»
и ἀριθμός — «число», «показатель»
Поистине безграничны приложения показательной и
логарифмической функций в самых различных областях науки и техники, а ведь придумывали логарифмы для облегчения вычислений. Через четыре года будет четыре столетия с того дня, как в 1614 году были опубликованы первые логарифмические таблицы, составленные Джоном Непером. Они помогли астрономам и инженерам, сокращая время на вычисления, и тем самым, как сказал знаменитый французский ученый Лаплас, «удлиняли жизнь вычислителям».Логарифмическая разминка
«Немного истории».
Слайд 11
Логарифмическая разминка
«Немного истории».
Параллельно с Непером
над составлением
таблицы логарифмов работал другой
любитель математики -
Йост Бюрги.Он был швейцарским часовщиком и
мастером астрономических приборов.
Бюрги составил таблицы логарифмов
раньше, но только в 1620 году издал свою
книгу "Таблицы арифметической и
геометрической прогрессии с обстоятельным
наставлением, как пользоваться ими при
всякого рода вычислениях".
Йост Бюрги
(1552 - 1632)
Слайд 12
Логарифмическая разминка
«Немного истории».
В 1623
г., т. е. всего через 9 лет после издания
первых таблиц, английским математиком Эдмундом
Гантером была изобретена первая логарифмическая
линейка, ставшая рабочим инструментом для многих
поколений вплоть до появления ЭВМ.
Слайд 13
Логарифмическая линейка
1622 год - Первый вариант
линейки разработал английский математик-любитель Уильям Отред
Слайд 15 Англичанин Роберт Биссакар (и независимо от него в
1657 году — С.Патридж) разработал прямоугольную логарифмическую линейку, конструкция
которой в основном сохранилась до наших дней.Слайд 16 Однако в начале XXI века логарифмические линейки получили
второе рождение в наручных часах. Дело в том, что,
следуя моде, производители дорогих и престижных марок часов перешли от электронных хронометров с ЖК-экранами к стрелочным и места для встраиваемого калькулятора оказалось недостаточно. Однако спрос на хронометры со встроенным вычислительным устройством среди следящих за модой людей заставил производителей часов выпустить модели с встроенной логарифмической линейкой, выполненной в виде вращающихся колец со шкалами вокруг циферблата. По прихоти производителей такие устройства обычно называются «навигационная линейка». Их достоинство — можно сразу, в отличие от микрокалькулятора, получить таблицу (например, расхода топлива на пройденное расстояние, перевода миль в километры и т. п.).
Слайд 17
Логарифмическая спираль
«Удивительное рядом»
Спираль – это плоская кривая
линия, многократно обходящая одну из точек на плоскости, которая
называется полюсом спирали.
Слайд 19
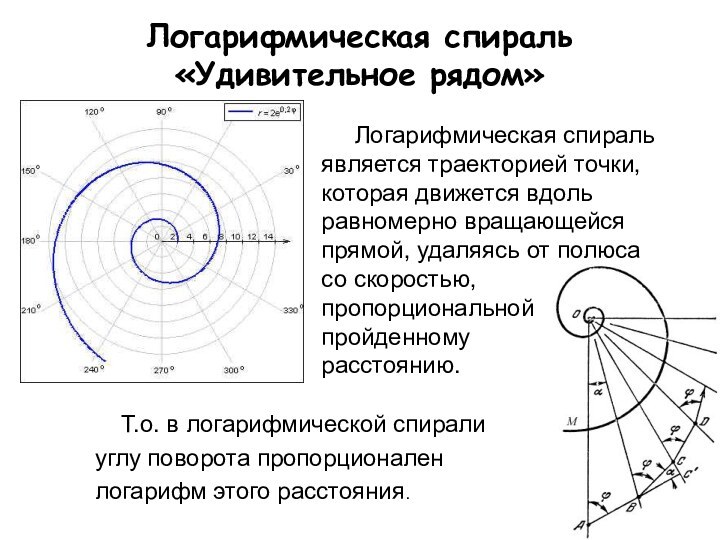
Логарифмическая спираль
«Удивительное рядом»
Логарифмическая спираль
является
траекторией точки, которая движется вдоль равномерно вращающейся прямой, удаляясь от полюса
со скоростью,
пропорциональной
пройденному
расстоянию.
Т.о. в логарифмической спирали
углу поворота пропорционален
логарифм этого расстояния.
Слайд 20
Логарифмическая спираль
«Удивительное рядом»
Первым ученым, открывшим эту удивительную
кривую, был
французский математик
Рене Декарт (1596-1650гг.)
Самое интересное и удивительное в том, что логарифмическая спираль возникает в нашей жизни в связи с самыми разными природными формами.
Слайд 21
Логарифмическая спираль
«Удивительное рядом»
По логарифмическим спиралям выстраиваются
цветки
в соцветиях подсолнечника
Слайд 22
Логарифмическая спираль
«Удивительное рядом»
По логарифмическим спиралям выстраиваются
рога
многих животных
Слайд 23 Живые существа обычно растут, сохраняя общее очертание своей
формы. При этом они растут чаще всего во всех
направлениях - взрослое существо и выше и толще детеныша. Но раковины морских животных могут расти лишь в одном направлении.Логарифмическая спираль
«Удивительное рядом»
Слайд 24
Логарифмическая спираль
«Удивительное рядом»
По логарифмической спирали свёрнуты
раковины
многих улиток и моллюсков.
Слайд 26
Логарифмическая спираль
«Удивительное рядом»
По логарифмической спирали формируется
тело циклона
Слайд 27
Логарифмическая спираль
«Удивительное рядом»
Даже пауки, сплетая паутину,
закручивают нити вокруг центра по логарифмической спирали.
Слайд 28
Логарифмическая спираль
«Удивительное рядом»
улитка
Человеческое ухо
– это маленькое чудо!
Улитка является органом, воспринимающим звук, в
котором самой природой заложенаЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ!
Слайд 29
Логарифмическая спираль
«Удивительное рядом»
Траектории насекомых
летящих на
свет также описывают логарифмическую спираль.
**************************
Логарифмическая спираль единственная из
спиралей не меняет своей формы при увеличении размеров. Видимо, это свойство и послужило причиной того, что в живой природе логарифмическая спираль встречается чаще других.
Слайд 30
Логарифмическая спираль
«Удивительное рядом»
По логарифмическим
спиралям закручены многие галактики, в частности Галактика, которой принадлежит
Солнечная система.
Слайд 31
И эту спираль мы повсюду встречаем:
к примеру,
ножи в механизме вращая. В изгибе трубы мы ее обнаружим
– турбины тогда максимально послужат!Логарифмическая спираль
«Удивительное рядом»
Слайд 32 Очертания, выраженные логарифмической спиралью, имеют не только раковины.
Спираль увидели в расположении семян подсолнечника, в шишках сосны,
ананасах, кактусах и т.д.
Слайд 36
«Логарифмы в музыке»
Музыканты редко увлекаются математикой; большинство из
них питают к этой науке чувство уважения. Между тем,
музыканты - даже те, которые не проверяют подобно Сальери у Пушкина («алгеброй гармонию»), - встречаются с математикой гораздо чаще, чем сами подозревают, и притом с такими «страшными» вещами, как логарифмы.
Слайд 37
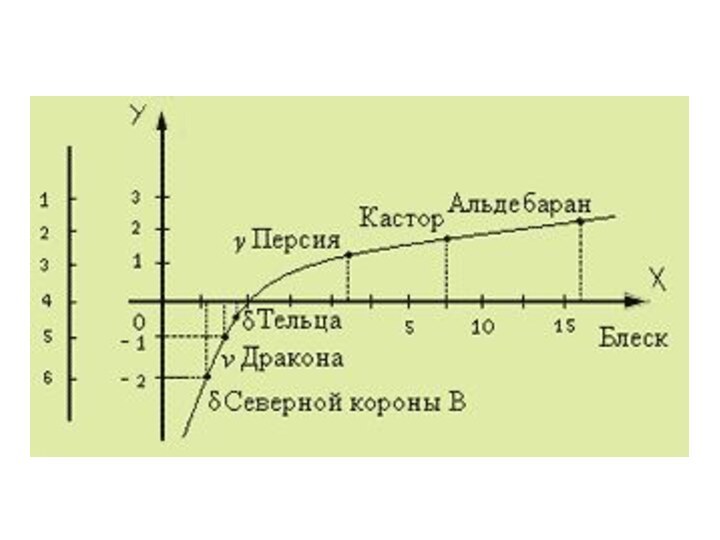
Звезды, шум и логарифмы
Этот заголовок связывает столь, казалось
бы, несоединимые вещи. Шум и звезды объединяются здесь потому,
что громкость шума и яркость звезд оцениваются одинаковым образом - по логарифмической шкале.
Слайд 39
Любимая цифра
Возьмите, пожалуйста, ручки и запишите свою
любимую
цифру.
Умножьте эту цифру на 9.
Полученное число умножьте
на 12345679 . Если вы все сделали правильно, то у Вас
получится букет из ваших любимых цифр.
А теперь припишите справа
к полученному числу 9 нулей.
Пусть у вас будет столько
счастливых дней!!!