- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку по алгебре по теме Теорема Виета
Содержание
- 2. Цели урока:Познакомить учащихся с теоремой Виета;Доказать утверждение,
- 3. Познакомимся с ещё одним способом решения квадратных
- 4. Задание: Какие из данных уравнений приведённые?
- 5. Вывод: Обе части уравнения
- 6. Франсуа Виет (1540-1603)Франсуа Виет — замечательный французский
- 7. Теорема Виета:Сумма корней приведённого квадратного уравнения равна
- 8. Справедливо утверждение, обратное теореме Виета: Если
- 9. Доказательство: По условию m+n=-p,
- 10. Рассмотрим примеры применения теоремы Виета и теоремы,
- 11. Решение: Дискриминант D=25-4*3*2=1
- 12. Тренировочные упражнения№ 573 а)-г) устно д)-з) письменно
- 13. Пример № 2. С помощью теоремы, обратной
- 14. Решим составленную систему подбором.Разложим число -15 на
- 15. Пример №2 (продолжение) х1+ х2 =2
- 16. Пример №3. Решить уравнение
- 17. Пример №3. Решить уравнение
- 18. Пример:№4. Решите квадратное уравнение, используя теорему Виета:
- 19. Выполните № 576.
- 20. Подведение итогов.По праву в стихах быть достойна
- 21. Скачать презентацию
- 22. Похожие презентации
Цели урока:Познакомить учащихся с теоремой Виета;Доказать утверждение, обратное теореме Виета;Рассмотреть примеры применения теоремы Виета и теоремы, обратной теореме Виета.




















Слайд 2
Цели урока:
Познакомить учащихся с теоремой Виета;
Доказать утверждение, обратное
теореме Виета;
теореме Виета.
Слайд 3
Познакомимся с ещё одним способом решения квадратных уравнений.
Данным
способом решаются приведённые квадратные уравнения
Квадратное уравнение ,в котором первый
коэффициент равен 1, называют приведённым квадратным уравнением.
Слайд 4
Задание: Какие из данных уравнений приведённые?
х2+ 3x-10=0
5х2-15x+5=0
х2-2x-1=02х2-9x+10=0
Как квадратное уравнение сделать приведённым?
х2-3x+1=0
х2-4,5x+5=0
Слайд 5
Вывод:
Обе части уравнения
aх2+ bx + c =0
разделим на первый
коэффициент aи получим приведённое уравнение
х2+px+q=0, где p= , q=
Слайд 6
Франсуа Виет (1540-1603)
Франсуа Виет — замечательный французский математик,
положивший начало алгебре как науке о преобразовании выражений, о
решении уравнений в общем виде, создатель буквенного исчисления. Виет первым стал обозначать буквами не только неизвестные, но и данные величины.
Слайд 7
Теорема Виета:
Сумма корней приведённого квадратного уравнения равна второму
коэффициенту, взятому с противоположным знаком, а произведение корней равно
свободному члену. х2+px+qx=0
х1+ х2=-p
х1* х2=q
Слайд 8
Справедливо утверждение, обратное теореме Виета:
Если числа
m и n таковы, что их сумма равна -p,
а произведение равно q, то эти числа являются корнями уравнения: х2+px+q=0
Слайд 9
Доказательство:
По условию m+n=-p,
а mn=q.
Значит, уравнение х2+pх+q=0 можно
записать в видех2 -(m+n) x+mn=0.
Подставив вместо x число m, получим:
m2-(m+n)m+mn=m2-m2-mn+mn=0.
Значит, число m является корнем уравнения.
Аналогично можно показать, что число n также является корнем уравнения.
Слайд 10 Рассмотрим примеры применения теоремы Виета и теоремы, обратной
теореме Виета.
Пример
№1Найдите сумму и произведение корней уравнения
3x2-5x+2=0.
Слайд 11
Решение:
Дискриминант D=25-4*3*2=1 -
положительное число. Значит, уравнение имеет корни. Эти же
корни имеет приведённое квадратное уравнение:х2- x+ =0.
Значит, сумма корней уравнения 3х2-5x+2=0
также равна ,а произведение равно .
Слайд 13 Пример № 2. С помощью теоремы, обратной теореме
Виета, решить уравнение х2
-2x- 15=0 Пусть х1 и х2 корни уравнения.
Составим систему
х1+ х2=2
х1* х2=-15
Внимание! При записи 1-го уравнения системы важно не совершить ошибку. Сумма корней равна -p.
Слайд 14
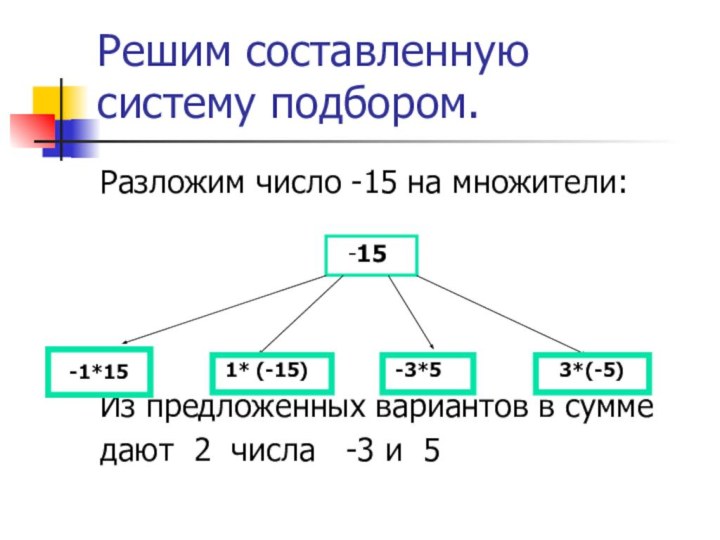
Решим составленную систему подбором.
Разложим число -15 на множители:
Из
предложенных вариантов в сумме
дают 2 числа -3 и
5 -15
-1*15
1* (-15)
-3*5
3*(-5)
Слайд 15
Пример №2 (продолжение)
х1+ х2 =2
-3+5=2
х1=-3х1х2=-15 -3*5=-15 х2=5
Ответ: корни уравнения -3 и 5.
Слайд 16 Пример №3. Решить уравнение
х2+5х+6=0
Решение: По теореме,
обратной теореме Виета, имеем:х1+х2=-5
х1*х2=6
Так как произведение корней –положительное число, то 1) оба множителя– отрицательные числа или 2) оба множителя - положительные числа. Сумма корней отрицательна, значит, возможен 1) случай.
Слайд 17 Пример №3. Решить уравнение
х2+5х+6=0
Решение:
По теореме, обратной теореме Виета, имеем:х1+х2=-5 х1=-2
х1*х2=6 х2=-3
Так как произведение корней –положительное число, то 1) оба множителя– отрицательные числа или 2) оба множителя - положительные числа. Сумма корней отрицательна, значит, возможен 1) случай. Нетрудно догадаться, что это числа - 2 и - 3.
ОТВЕТ: - 2 и - 3.
Слайд 18
Пример:№4. Решите квадратное уравнение, используя теорему Виета:
а) х2-5х+6=0
Ответ: х1=3, х2=2, т.к. 3х2=6 и 3+2=5 , -p=5, q=6
б) х2+3х-4=0
Ответ: х1=-4, х2=1, т.к. -4х1=-4 и 4+1=-3, p=3, q=-4.
Слайд 20
Подведение итогов.
По праву в стихах быть достойна воспета,
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства
такого:Умножишь ты корни и дробь уж готова
В числителе с, в знаменателе а.
А сумма корней тоже дроби равна,
Хоть с минусом дробь эта- что за беда,
В числителе в, в знаменателе а.
aх2 + bx + c =0
х1 * х2 = с/а,
х1 + х2 = - в/а