Слайд 2
Дидактическая цель:
Создать условия для осознания и осмысления вывода
формулы n-го члена геометрической прогрессии.
Цели по
содержанию урока:
Образовательная – способствовать осознанию того, что тема, изученная на уроке математики применяется на уроках биологии.
Развивающая – способствовать обучению школьников умению выделять математическую модель из практико-ориентированной задачи.
Воспитательная – способствовать эстетическому и экологическому воспитанию учащихся.
Слайд 3
Тип урока – изучение нового материала.
Форма организации познавательной
деятельности –
фронтальная, групповая, индивидуальная.
Методы – проблемного изложения материала,
частично-поисковый.
Оборудование: компьютер и мультимедийный проектор, наглядный материал (таблицы), тетрадь.
Слайд 4
Здравствуйте , ребята! Сегодня мы с вами проведём
необычный урок, на котором вам понадобятся знания не только
по математике, но и по биологии. На пути сегодняшнего урока вам встретятся необычные задания и путешествие в страну микроорганизмов…
Удачи!
Слайд 5
О каком свойстве организмов идёт речь?
Жизнь замечательных растений
Слайд 6
Тема сегодняшнего урока…
Возможности организмов и геометрическая прогрессия.
Слайд 7
В какое время года и каким способом размножается
инфузория-туфелька?
Летом инфузории размножаются бесполым способом деления пополам.
Сколько будет инфузорий
после второго размножения?
4
Сколько после третьего размножения?
8
Сколько после 15 размножения?
???
Слайд 8
Рассмотрим последовательность размножений:
1; 2; 4; 8; 16;32; 64;
…
Какое предположение можно сделать, анализируя данную последовательность?
Это геометрическая прогрессия,
первый член которой равен 2 и знаменатель равен 2.
Слайд 9
Как вы определили, что это геометрическая прогрессия?
Геометрическая прогрессия
–это числовая последовательность
b1, b2, b3, …, bn, …
если для всех натуральных n выполняется равенство
bn+1 = bn*q
где q - некоторое число
bn ≠ 0
qn ≠ 0
Слайд 10
Что нам нужно знать для ответа на вопрос:
«Сколько инфузорий будет после 15 размножения?»
Нужно в каждом
случае найти n-й член прогрессии.
Можно ли упростить процесс вычисления?
Нужно вывести формулу n- члена геометрической прогрессии.
Слайд 11
Задание 1
найти второй, третий, четвертый, пятый члены геометрической
прогрессии общего вида через взаимосвязь между соседними членами;
Задание 2
сделать
замену b1 и q;
Задание 3
вывести формулу n-го члена
Слайд 12
По определению геометрической прогрессии:
b2 = b1*q
b3 = b2+1
=b2*q=b1*q*q =b1*q2
b4 = b3+1 =b3*q=b1*q2*q =b1*q3
b5 = b4+1 =b4*q=b1*q3*q =b1*q4
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
bn = b1*qn-1
Формула n-го члена
Слайд 13
«Сколько инфузорий будет после 15 размножения? »
После 15 размножения при идеальном условии выживания инфузорий будет:
b15 = 2∙ 214 = 32768.
Слайд 14
Способность к размножению у бактерий настолько велика, что
еслибы они не гибли по разным причинам, а беспрерывно
размножались, то за трое суток общая масса потомства только одной бактерии могла бы составить 7500 тонн. Таким громадным количеством бактерий можно заполнить 375 железнодорожных вагонов.
Слайд 15
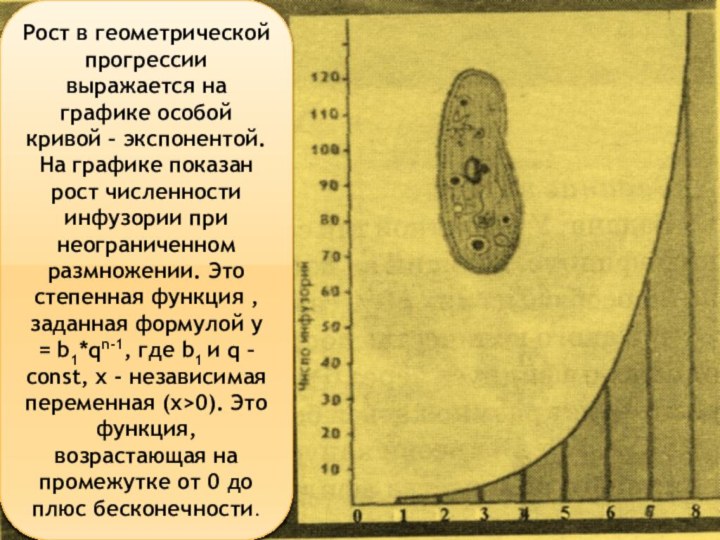
Рост в геометрической прогрессии выражается на графике особой
кривой – экспонентой. На графике показан рост численности инфузории
при неограниченном размножении. Это степенная функция , заданная формулой y = b1*qn-1, где b1 и q – const, х - независимая переменная (х>0). Это функция, возрастающая на промежутке от 0 до плюс бесконечности.
Слайд 17
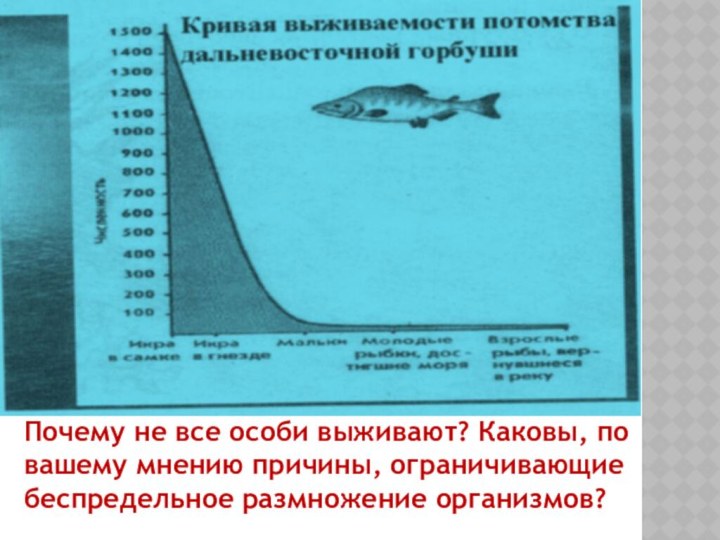
Почему не все особи выживают? Каковы, по вашему
мнению причины, ограничивающие беспредельное размножение организмов?
Слайд 18
Почему из всех птиц человек разводит преимущественно представителей
отряда курообразных и гусеобразных? Известно. Что по качеству мяса,
скорости роста, размерам, степени привыкания к человеку им не уступают ни дрофы, ни кулики, ни голуби.
Слайд 19
задача. Одно растение одуванчика занимает на земле площадь
1 м2 и даёт в год около ста летучих
семян.
а) Сколько кв. километров площади покроет всё потомство одной особи одуванчика через 10 лет при условии, если он размножается беспрепятственно по геометрической прогрессии?
б) Хватит ли этим растениям на 11-й год места на поверхности суши земного шара, если площадь суши 148 млн. км2.
Слайд 20
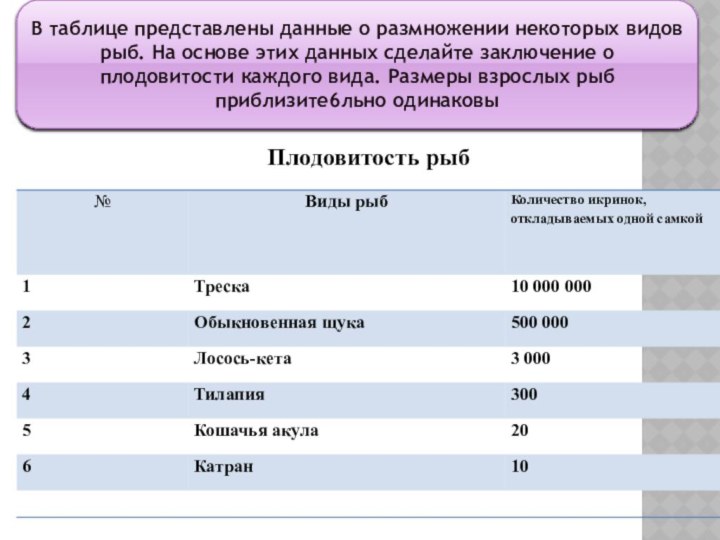
В таблице представлены данные о размножении некоторых видов
рыб. На основе этих данных сделайте заключение о плодовитости
каждого вида. Размеры взрослых рыб приблизите6льно одинаковы
Слайд 21
Выберите правильное утверждение.
Численность любого вида при отсутствии ограничений
(обилие пищи, обилие мест обитания, отсутствия врагов и т.д.)
растёт в соответстви…
А. С арифметической прогрессией.
Б. С прямой пропорциональной зависимостью.
В. С геометрической прогрессией.
Г. С обратной пропорциональной зависимостью.
Т
Е
С
Т
Слайд 22
Выберите правильное утверждение.
2. Кривая роста численности (зависимость
численности от времени) любого вида при отсутствии ограничений называется
…
А. Гиперболой.
Б. Прямой.
В. Параболой.
Г. Экспонентой
Т
Е
С
Т
Слайд 23
Выберите правильное утверждение.
3. Бактерии способны очень быстро
размножаться. Каждые полчаса из одной клетки появляются две. Если
одну бактерию поместить в идеальные условия с обилием пищи, то за сутки её потомство должно составить 248 = 281 474 976 710 656 клеток. Такое количество бактерий занимает 0,25-литровый стакан. Подумайте, за какое время их количество удвоитсяи займёт пол-литровый объём. Выберите правильный ответ.
А. Одни сутки.
Б. Один час.
В. Двое суток.
Г. Полчаса
Т
Е
С
Т
Слайд 25
Достигли ли
цели урока?
Что нового узнали
на уроке?
Где
могут пригодится
полученные знания?
Над чем необходимо поработать дома?
Слайд 26
Спасибо за урок!
!
Домашнее задание?
Задача. У капустной тли свой
паразит – наездник афидиус, дающий за лето более 6
поколений по 30 особей (из них 50% самцов) в каждом.
а) Какого количества достигнет всё потомство от одного афадиуса через 6 месяцев, если этот паразит будет размножаться беспрепятственно?
б) Хватит ли к осени капустных тлей для питания такого количества афидиусов, если афидиус своё яйцо откладывают только в одну тлю?
Вот оно::