Презентация на тему по математике История возникновения понятия степень числа

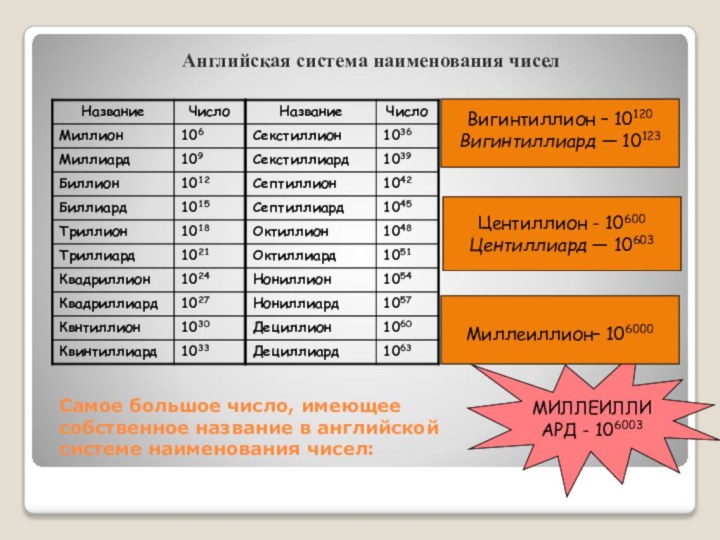
Междуречья встречаются задачи на вычисление степеней
«Квадрат и другой квадрат,

сторона которого есть , стороны первого квадрата, имеют вместе площадь 100. Вычисли мне это».
Задача из Московского папируса

История возникновения степени числа

100 изображались специальными значками - иероглифами. Для записи чисел

они употребляли следующие иероглифы:

то, что когда происходит умножение какого-либо числа на одно

и то же число много раз, то на это тратится огромное количество ненужных усилий. Более того, такая операция вела к значительным финансовым затратам: согласно действовавшим тогда установкам на оформление любых записей, каждой действие с числом должно было подробно описываться. Если вспомнить, что даже самый простейший папирус стоил весьма внушительную сумму денег, то не стоит удивляться тем усилиям, которые египтяне приложили, чтобы найти выход из этой ситуации.

натуральные степени чисел
«Все числа… состоят из некоторого

количества единиц; ясно, что они продолжаются, увеличиваясь до бесконечности. …среди них находятся: квадраты, получающиеся от умножения некоторого числа самого на себя; это же число называется стороной квадрата, затем кубы, получающиеся от умножения квадратов на их сторону, далее квадрато-квадраты — от умножения квадратов самих на себя, далее квадрато-кубы, получающиеся от умножения квадрата на куб его стороны, далее кубо-кубы — от умножения кубов самих на себя».

сократить число символов. Книга Михеля Штифеля «Полная арифметика» (1544

г.) сыграла в этом значительную роль.
«Сумма знаний…» Луки Пачоли была одним из первых опубликованных сочинений. Но математики продолжали искать более простую систему обозначений так как его обозначения были не удобны.
Француз, бакалавр медицины Никола Шюке (? - около 1500 г.) смело ввёл в свою символику не только нулевой, но и отрицательный показатель степени. Он писал его мелким шрифтом сверху и справа от коэффициента.

«Алгебре» использовал ту же идею. Он обозначал неизвестное специальным

символом 1, а символами 2, 3,... - его степени. Обозначения Бомбелли также оказали влияние и на символику нидерландского математика Симона Стевина (1548—1620). Он обозначал неизвестную величину кружком О, внутри которого указывал показатели степени. Стевин предложил называть степени по их показателям - четвёртой, пятой и т. Д. и отверг Диофантовы составные выражения «квадрато-квадрат», «квадрато-куб».

степеней а2,а3,... Любопытно, что Декарт считал, что а∙а не

занимает больше места, чем а2 и не пользовался этим обозначением при записи произведения двух одинаковых множителей. Немецкий ученый Лейбниц считал, что упор должен быть сделан на необходимости применения символики для всех записей произведений одинаковых множителей и применял знак а2.

10603


МИЛЛЕИЛЛИАРД - 106003





Миллеиллион– 106000


Самое большое число, имеющее собственное название

в английской системе наименования чисел:

Английская система наименования чисел

степени числа 10