Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по алгебре к уроку Исследование функции на монотонность (10 класс)

Содержание

Что обозначают математические символы?f(x), D(y),f ´ (x), E(y), (xn )´, (u·v)´, (c)´ ,f ´(x)f(x)+хх1х2+-
Что обозначают математические символы?f(x), D(y),f ´ (x), E(y), (xn )´, (u·v)´, (c)´ ,f ´(x)f(x)+хх1х2+- Тема занятия: Исследование функции на монотонность с помощью производнойЗадачи:определить алгоритм исследования Способы исследования функции на монотонность Графический.С помощью свойств числовых неравенств.С помощью производной. Общая схема исследования функции и построение графикаПостроить график.Найти точки пересечения графика с Общая схема исследования функции и построение графикаНайти область определения.Найти точки пересечения графика Теоретическая основа Достаточный признак возрастания (убывания) функции.Если f´(x)>0 в каждой точке интервала Домашнее заданиеИсторическая справка: о Фридрихе Лейбнице (1646-1716);о Иоганне Бернулли (1667-1748). Алгоритм исследования Найти f´(x).f´(x)=0 (найти нули производной).Оформить эскиз: знаки производной и поведение функции по монотонности. Исследовать функцию на монотонность – это значит выяснить, на каких промежутках области Задание ЕГЭ – 2017 Функция y=f(x) задана на (-3;8).На рисунке изображен график Определите функцию, исходя из её «автобиографии»D(y)=R;E(y)=[0;+∞);Функция общего вида;Функция Домашнее задание:Исследовать функцию на монотонность (индивидуальные задания);Нестандартное задание: найти функции, описывающие реальные СПАСИБО ЗА РАБОТУ!
Слайды презентации

Слайд 2

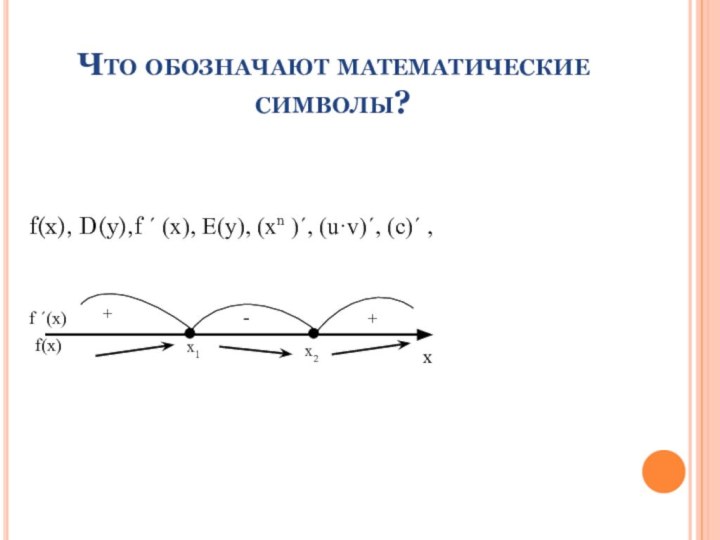
Слайд 3 Что обозначают математические символы?
f(x), D(y),f ´ (x), E(y),

Что обозначают математические символы?f(x), D(y),f ´ (x), E(y), (xn )´, (u·v)´, (c)´ ,f ´(x)f(x)+хх1х2+-

(xn )´, (u·v)´, (c)´ ,





f ´(x)

f(x)
+
х
х1
х2
+
-

Слайд 4 Тема занятия: Исследование функции на монотонность с помощью

Тема занятия: Исследование функции на монотонность с помощью производнойЗадачи:определить алгоритм исследования

производной
Задачи:
определить алгоритм исследования функции на монотонность с помощью производной;

используя алгоритм, исследовать функции по монотонности;
формировать глубину и оперативность математического мышления.

Слайд 5 Способы исследования функции на монотонность
Графический.
С помощью свойств

Способы исследования функции на монотонность Графический.С помощью свойств числовых неравенств.С помощью производной.

числовых неравенств.
С помощью производной.

Слайд 6 Общая схема исследования функции и построение графика
Построить график.
Найти

Общая схема исследования функции и построение графикаПостроить график.Найти точки пересечения графика

точки пересечения графика с осями координат.
Найти интервала знакопостоянства функции.
Выяснить

чётность.
Найти область определения.
Найти асимптоты графика функции.
Найти интервалы монотонности функции.
Найти экстремумы функции.
Найти интервалы выпуклости и точки перегиба графика функции.

Слайд 7 Общая схема исследования функции и построение графика
Найти область

Общая схема исследования функции и построение графикаНайти область определения.Найти точки пересечения

определения.
Найти точки пересечения графика с осями координат.
Найти интервала знакопостоянства

функции.
Выяснить чётность.
Найти асимптоты графика функции.
Найти интервалы монотонности функции.
Найти экстремумы функции.
Найти интервалы выпуклости и точки перегиба графика функции.
Построить график.

Слайд 8 Теоретическая основа
Достаточный признак возрастания (убывания) функции.

Если f´(x)>0

Теоретическая основа Достаточный признак возрастания (убывания) функции.Если f´(x)>0 в каждой точке

в каждой точке интервала X, то функция возрастает на

интервале.

Если f´(x)<0 в каждой точке интервала X, то функция убывает на интервале.


Слайд 9 Домашнее задание
Историческая справка:
о Фридрихе Лейбнице (1646-1716);
о Иоганне

Домашнее заданиеИсторическая справка: о Фридрихе Лейбнице (1646-1716);о Иоганне Бернулли (1667-1748).

Бернулли (1667-1748).

Слайд 10 Алгоритм исследования
Найти f´(x).
f´(x)=0 (найти нули производной).
Оформить эскиз:

Алгоритм исследования Найти f´(x).f´(x)=0 (найти нули производной).Оформить эскиз: знаки производной и поведение функции по монотонности.

знаки производной и поведение функции по монотонности.

Слайд 11 Исследовать функцию на монотонность – это значит выяснить,

Исследовать функцию на монотонность – это значит выяснить, на каких промежутках


на каких промежутках области определения функция возрастает,
на каких

убывает.

Слайд 12 Задание ЕГЭ – 2017
Функция y=f(x) задана на

Задание ЕГЭ – 2017 Функция y=f(x) задана на (-3;8).На рисунке изображен

(-3;8).
На рисунке изображен график её производной.
Исследуйте функцию на монотонность:


укажите количество промежутков, на которых функция убывает;
укажите количество промежутков, на которых функция возрастает;
Найти длину промежутков возрастания (убывания) этой функции.

Слайд 13 Определите функцию, исходя из её «автобиографии»
D(y)=R;
E(y)=[0;+∞);
Функция общего вида;
Функция

Определите функцию, исходя из её «автобиографии»D(y)=R;E(y)=[0;+∞);Функция общего вида;Функция xЄ

xЄ [0,5;+∞),

Функция xЄ (-∞; 0,5].

y=(2x-1)3;
y=(2x-1)2;
y=2x-1;

Слайд 14 Домашнее задание:
Исследовать функцию на монотонность (индивидуальные задания);
Нестандартное задание:

Домашнее задание:Исследовать функцию на монотонность (индивидуальные задания);Нестандартное задание: найти функции, описывающие

найти функции, описывающие реальные физические процессы, которые изучали на

уроках физика и исследовать их по схеме.

  • Имя файла: prezentatsiya-po-algebre-k-uroku-issledovanie-funktsii-na-monotonnost-10-klass.pptx
  • Количество просмотров: 248
  • Количество скачиваний: 6
- Предыдущая Презентация по английскому языку
Следующая - Презентация Певец земли донской

Похожие презентации

Что такое степень с натуральным показателем Что такое степень с натуральным показателем 162
Презентация по алгебре и началам анализа на тему Начала статистики (10 класс) Презентация по алгебре и началам анализа на тему Начала статистики (10 класс) 183
Презентация к уроку по алгебре на тему: Решение задач с помощью уравнений (по материалам Бородинского сражения) Презентация к уроку по алгебре на тему: Решение задач с помощью уравнений (по материалам Бородинского сражения) 162
Решу ЕГЭ: планиметрия, решение прямоугольных треугольников(профиль), часть 1 Решу ЕГЭ: планиметрия, решение прямоугольных треугольников(профиль), часть 1 166
Презентация по алгебре на тему Что такое алгебраические дроби. Презентация по алгебре на тему Что такое алгебраические дроби. 169
Шаблоны презентаций ЕГЭ Шаблоны презентаций ЕГЭ 186
Функции и их графики Функции и их графики 405
Решение задач с помощью дробных рациональных уравнений Решение задач с помощью дробных рациональных уравнений 159
Неравенства с двумя переменными Неравенства с двумя переменными 170
Модуль Модуль 176
Электронное пособие по математике Интегральное исчисление Электронное пособие по математике Интегральное исчисление 195
Алгебра логики Алгебра логики 195
Аркфункции Аркфункции 173
Первый урок алгебры в 7 классе Первый урок алгебры в 7 классе 201
Урок по теме Решение квадратных уравнений Урок по теме Решение квадратных уравнений 137
Презентация по математике на тему Графики функций, содержащих модуль (9 класс) Презентация по математике на тему Графики функций, содержащих модуль (9 класс) 183
Функция. Область определения и область значений функции Функция. Область определения и область значений функции 167
Линейная зависимость векторов Линейная зависимость векторов 238
Презентация к уроку алгебры Формулы сокращённого умножения (7 класс) Презентация к уроку алгебры Формулы сокращённого умножения (7 класс) 197
Презентация по алгебре по теме Сложение графиков при решении задач с параметрами Презентация по алгебре по теме Сложение графиков при решении задач с параметрами 146
погрешность погрешность 190
Чертежи к задачам по стереометрии. Глава 3. Многогранники. Пирамида. (10 класс) Чертежи к задачам по стереометрии. Глава 3. Многогранники. Пирамида. (10 класс) 165
Вероятность случайного события Вероятность случайного события 303
Презентация к уроку Возведение в квадрат суммы и разности двух выражений Презентация к уроку Возведение в квадрат суммы и разности двух выражений 191
Презентация по математике Простейшие вероятностные задачи (10 класс) Презентация по математике Простейшие вероятностные задачи (10 класс) 172
Презентация по математике Математика и космос Презентация по математике Математика и космос 208
Вписанные, центральные углы Вписанные, центральные углы 216
Презентация по алгебре на тему Степень и её свойства, одночлен, многочлен (8 класс) Презентация по алгебре на тему Степень и её свойства, одночлен, многочлен (8 класс) 210
Презентация Примеры применения производной (алгебра и начала анализа. 10 класс) Презентация Примеры применения производной (алгебра и начала анализа. 10 класс) 168
Прогрессии в жизни Прогрессии в жизни 245