Презентация на тему по математике на тему Понятие действительного числа (10 класс Никольский)

множества
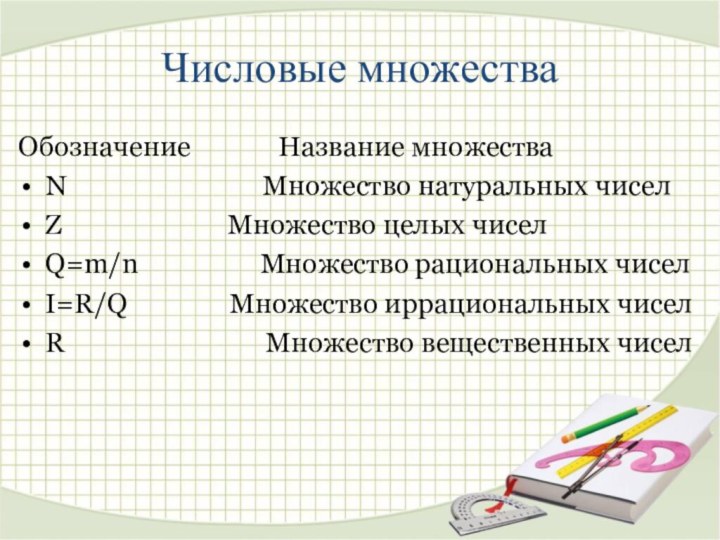
N

Множество натуральных чисел
Z Множество целых чисел
Q=m/n Множество рациональных чисел
I=R/Q Множество иррациональных чисел
R Множество вещественных чисел

Числовые множества

N={1,2,…n,…}.
Заметим, что множество натуральных чисел замкнуто относительно сложения и

умножения, т.е. сложение и умножение выполняются всегда, а вычитание и деление в общем случае не выполняются

1) число 0 (ноль),
2) число (-n), противоположное

натуральному n.
При этом полагаем: n+(-n)=(-n)+n=0,
-(-n)=n.
Тогда множество целых чисел можно записать так:
Z ={…,-n,…-2,-1,0,1,2,…,n,…}.
Заметим также, что:
Это множество замкнуто относительно сложения, вычитания и умножения, т.е.
Из множества целых чисел выделим два подмножества:
1) множество четных чисел
2) множество нечетных чисел

виде:

В частности,

Таким образом,
Множество рациональных чисел замкнуто относительно сложения, вычитания, умножения и деления (кроме случая деления на 0).

гипотенузу прямоугольного треугольника с катетам

.
По теореме Пифагора гипотенуза будет равна .
Но число не будет рациональным, так как ни для каких m и n.
Нельзя решить уравнение .
Нельзя измерить длину окружности и т.д.
Заметим, что всякое рациональное число можно представить в виде конечной или бесконечной периодической десятичной дроби.

будем называть иррациональными.
Множество иррациональных чисел обозначим

I.

Для иррациональных чисел нет единой формы обозначения. Отметим два иррациональных числа, которые обозначаются буквами – это числа и е.

называется неотрицательное действительное число:
| 5 | = 5
|– 5

| = 5

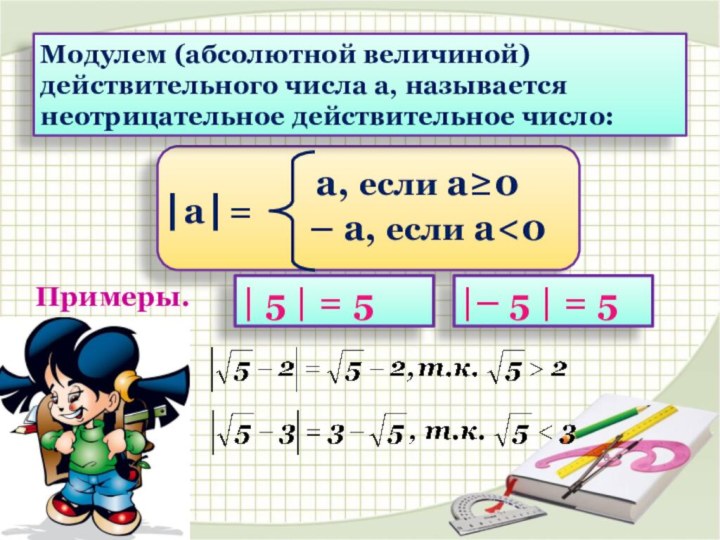
а =

а, если а≥0

– а, если а<0

3
–(– 3) = 3
– 2,1
–(– 2,1)

= 2,1

а + 3

–а– 3

2а – 7

7 – 2а

4
0
0
– 8,7
8,7
а²
а²

| + | – 5 | = ___
2)

| – 6 | + | 6 | = __

3) 9 ∙ | 5 – 7 | = ___

4) | 10 – 10 | ∙ 7 = __

5) – 3 ∙ | – 4 | = ___

5) | – 18 | : | – 3 | = _

10

12

18

0

–12

6

– m

m

а ≥ 0

а < 0

| = а
Модуль действительного числа а есть расстояние (в

единичных отрезках) от точки с координатой а на числовой оси до начала координат.

– 8,5|,
если 5,6≤ х ≤8,2
Пример №3
Упростить выражение