Слайд 2
1. Показательная функция.
2. Экспонента.
3. Показательной
функции и её применеие в природе и технике.
4.
В биологии.
5. В экономике.
Слайд 3
Презентация по теме: «Показательная функция».
Некоторые наиболее часто
встречающиеся
виды
трансцендентных функций,
прежде всего показательные,
открывают доступ ко
многим исследованиям.
Л.Эйлер.
Слайд 4
Показательная функция.
Функция вида у=ах ,где а-заданное число, а>0,
а≠1, х-переменная, называется показательной.
Слайд 5
Показательная функция обладает следующими свойствами:
Д(у): множество R всех
действительных чисел;
Е(у):множество всех положительных чисел;
Показательная функция у=ах является возрастающей
на множестве всех действительных чисел,если а>1,и убывающей,если 0<а<1;
Не является ни четной, ни нечетной;
Не ограничена сверху,ограничена снизу;
Не имеет ни наибольшего, ни наименьшего значения;
Непрерывна;
Если а>1 ,то функция выпукла вниз.
Слайд 6
Графики функции у=2х и у=(½)х
График функции у=2х
проходит через точку (0;1) и расположен выше оси Ох.
а>1
Д(у): х є R
Е(у): у >0
Возрастает на всей области определения.
График функции у= также проходит через точку (0;1) и расположен выше оси Ох.
0<а<1 Д(у): х є R
Е(у): у>0
Убывает на всей области определения.
Слайд 7
Показательные уравнения.
Уравнения,у которых неизвестное находится в показателе степени,
называются показательными.
Способы решения:
По свойству степени;
Вынесение общего множителя за скобки;
Деление
обеих частей уравнения на одно и то же выражение,принимающее значение отличное от нуля при всех действительных значениях х;
Способ группировки;
Сведение уравнения к квадратному;
Графический.
.
Например:
Слайд 8
Используя свойства возрастания и убывания показательной функции, можно
сравнить числа и решать показательные неравенства.
Сравнить:
а) 53 и 55;
б) 47 и 43; в) 0,22 и 0,26; г) 0,92 и 0,9.
Решить:
а) 2х>1; б) 13х+1<133; в) 0,7х-2>0,7; г) 0,04х<0,22.
Неравенства, у которых неизвестное находится в показателе степени, называются показательными.
Решение показательных неравенств сводится к решению неравенств ах>ав или ах<ав.
Если а>1, то х>в (х<в).
Если 0<а<1. то х<в (х>в).
Способы решения показательных неравенств.
1.
По свойству степени;
2. Вынесение общего множителя за скобки;
3.Сведение к квадратному;
4. Графический.
Некоторые показательные неравенства заменой ах=t сводятся к квадратным неравенствам,которые решают,учитывая,что t>0.
Слайд 11
Решение систем показательных уравнений и неравенств.
Слайд 13
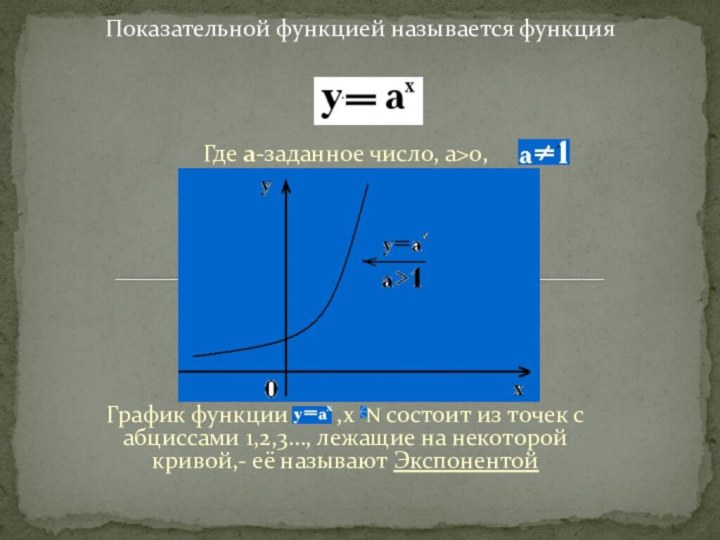
Где a-заданное число, а>о,
График функции
,х N состоит из точек с абциссами 1,2,3…, лежащие
на некоторой кривой,- её называют Экспонентой
Показательной функцией называется функция
Слайд 14
Экспонента (exp) — функция exp(x) = e, где
e — основание натуральных логарифмов.
Основные свойства
Экспонента определена на всей
вещественной оси. Она всюду возрастает и больше нуля. Обратная функция к ней — логарифм.
Экспонента бесконечно дифференцируема. Ее производная в нуле равна 1, поэтому касательная в этой точке проходит по углом 45°.
Основное функциональное свойство экспоненты: exp(a + b) = exp(a)exp(b). Непрерывная функция с таким свойством либо тождественно равна 0, либо имеет вид exp(ct), где c — некоторая константа.
Дифференциальные уравнения
Экспонента является решением дифференциального уравнения y' = y с граничным условием y(0) = 1. Кроме того через экспоненту выражаются общие решения однородных дифференциальных уравнений.
Формальное определение
Экспоненциальная функция может быть определена двумя эквивалентными способами. Через ряд Тейлора:
или через предел:
Здесь x — любое вещественное, комплексное, p-адическое число или ограниченный линейный оператор.
Слайд 15
Многообразные применения показательной (или как еще ее называют
экспонентой) функции вдохновили английского поэта Элмера Брила, он написал
«Оду экспоненте»
…Ею порождено многое из того,
Что достойно упоминания,
Как говорили наши
Англосаксонские предки.
Могущество ее порождений
Заранее обусловлено ее
Собственной красотой и силой,
Ибо они суть, физическое воплощение
Абстрактной идеи ее.
Английские моряки любят и знают ее
Под именем «Гунтер»
Две шкалы «Гунтера»-
Вот чудо изобретательности.
Экспонентой порождена
Логарифмическая линейка:
У инженера и астронома не было
Инструмента полезнее, чем она.
Даже изумные искусства питаются ею.
Разве музыкальная гамма не есть
Набор передовых логарифмов?
И таким образом абстрактно красивое
Стало предком одного из величайших
Человеческих достижений»
Были поэты, которые не посвящали од экспоненте, но упоминали их в своих стихах, Например, поэт Борис Слуцкий в стихотворении «Физики и лирики».
Слайд 16
И её применение в природе и технике.
Показательная функция
Слайд 17
Наглядный бытовой пример!
Все, наверное, замечали, что если снять
кипящий чайник с огня, то сначала он быстро остывает,
а потом остывание идет гораздо медленнее. Дело в том, что скорость остывания пропорциональна разности между температурой чайника и температурой окружающей среды. Чем меньше становится эта разность, тем медленнее остывает чайник. Если сначала температура чайника равнялась То, а температура воздуха T1, то через t секунд температура Т чайника выразится формулой:
T=(T1-T0)e-kt+T1,
где k - число, зависящее от формы чайника, материала, из которого он сделан, и количества воды, которое в нем находится.
Слайд 18
При падении тел в безвоздушном пространстве скорость их
непрерывно возрастает.
При падении тел в воздухе скорость падения тоже
увеличивается, но не может превзойти определенной величины.
Слайд 19
Рассмотрим задачу о падении парашютиста. Если считать, что
сила сопротивления воздуха пропорциональна скорости падения парашютиста, т.е. что
F=kv , то через t секунд скорость падения будет равна: v=mg/k(1-e-kt/m), где m - масса парашютиста. Через некоторый промежуток времени е-kt/m станет очень маленьким числом, и падение станет почти равномерным. Коэффициент пропорциональности k зависит от размеров парашюта. Данная формула пригодна не только для изучения падения парашютиста, но и для изучения падения капли дождевой воды, пушинки и т.д.
Слайд 20
Много трудных математических задач приходится решать в теории
межпланетных путешествий. Одной из них является задача об определении
массы топлива, необходимого для того, чтобы придать ракете нужную скорость v. Эта масса М зависит от массы m самой ракеты (без топлива) и от скорости v0, с которой продукты горения вытекают из ракетного двигателя.
Слайд 21
Если не учитывать сопротивление воздуха и притяжение Земли,
то масса топлива определиться формулой: M=m(ev/v0-1) (формула К.Э.Циалковского). Например,
для того чтобы ракете с массой 1,5 т придать скорость 8000 м/с, надо при скорости истечения газов 2000 м/с взять примерно 80 т топлива.
Слайд 22
Если при колебаниях маятника, гири, качающейся на пружине,
не пренебрегать сопротивлением воздуха, то амплитуда колебаний становится все
меньше, колебания затухают. Отклонения точки, совершающей затухающие колебания, выражается формулой: s=Ae-ktsin(?t+?). Так как множитель е-kt уменьшается с течением времени, то размах колебаний становится все меньше и меньше.
Слайд 23
Когда радиоактивное вещество распадется, его количество уменьшается. Через
некоторое время остается половина первоначального количества вещества. Этот промежуток
времени to называется периодом полураспада. Вообще через t лет масса m вещества будет равна: m=m0(1/2)t/t0, где m0 - первоначальная масса вещества. Чем больше период полураспада, тем медленнее распадается вещество.
Явление радиоактивного распада используется для определения возраста археологических находок, например, определен примерный возраст Земли, около 5,5 млрд. лет, для поддержания эталона времени.
Слайд 24
Задача:
Период полураспада плутония равен 140 суткам. Сколько плутония
останется через 10 лет, если его начальная масса равна
8г ?
Слайд 25
Как видите, во всех
приведенных выше исследованиях использовалась показательная
функция.
Слайд 26
Вот некоторые из Нобелевских лауреатов, получивших премию за
исследования в области физики с использованием показательной функции:
Пьер Кюри
- 1903 г.
Ричардсон Оуэн - 1928 г.
Игорь Тамм - 1958 г.
Альварес Луис - 1968 г.
Альфвен Ханнес - 1970 г.
Вильсон Роберт Вудро - 1978 г.
Слайд 27
Она не перестаёт нас удивлять!
Показательная функция также используется
при решении некоторых задач судовождения, например, функцию е-x используют
в задачах, требующих применения биноминального закона (повторение опытов), закона Пуассона (редких событий), закона Релея (длина случайного вектора).
Слайд 28
Применение показательной функции
в биологии .
Слайд 29
Применение логарифмической
функции в биологии.
В питательной среде бактерия
кишечной палочки делится каждую минуту. Понятно, что общее число
бактерий за каждую минуту удваивается. Если в начале процесса была одна бактерия, то через х минут их число (N) станет равной 2х , т.е.
N(х) = 2х.
Слайд 30
Применение показательной функции в экономике.
Слайд 31
Задача:
Ежемесячно на банковский вклад, равный S0 рублей начисляется
р%. На сколько процентов возрастет банковский вклад за х
месяцев?
Решение.