- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема о трёх перпендикулярах
Содержание
- 2. Установите по рисункам положение прямых a и bАВСD – прямоугольник,BF⊥(ABC)АВСD – прямоугольник,BF⊥(ABC)
- 3. Установите по рисункам положение прямых а и вАВСD – ромб,BF⊥(ABC)АВСD – ромб,BF⊥(ABC)
- 4. Основная цель:Сформировать навык применения теоремы о трёх перпендикулярах к решению задач.
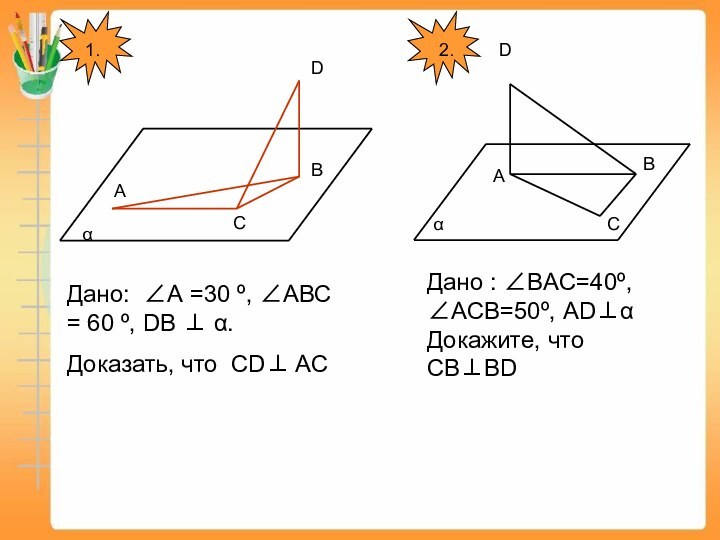
- 5. 1.Дано: ∠А =30 º, ∠АВС = 60 º, DB ⊥ α.Доказать, что CD⊥ AC
- 6. 3.АМ⊥ (АВС), АВ=АС, СD=DBДокажите, что МD⊥BC4.АВСD – параллелограмм, ВМ ⊥ (АВС), МС⊥DСОпределите вид параллелограмма АВСD
- 7. 5.АВСD – параллелограмм, СМ⊥(АВС), МО ⊥ ВDОпределите
- 8. №149Дано: АD⊥(АВС), Δ АВС- равнобедренный, АВ=АС= 5см,
- 9. № 150Дано: АВСD - прямоугольник, АК⊥(АВС), КD
- 10. №159 Плоскости (АDМ) и (ВСМ) имеют
- 11. Скачать презентацию
- 12. Похожие презентации
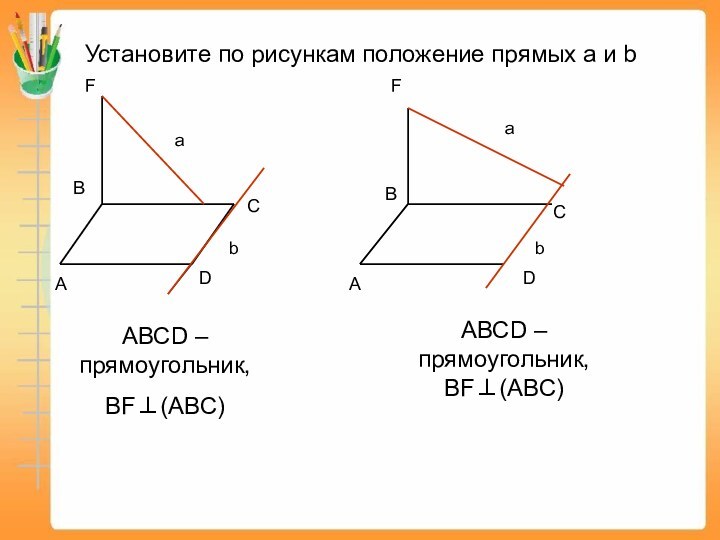
Установите по рисункам положение прямых a и bАВСD – прямоугольник,BF⊥(ABC)АВСD – прямоугольник,BF⊥(ABC)









Слайд 6
3.
АМ⊥ (АВС), АВ=АС, СD=DB
Докажите, что МD⊥BC
4.
АВСD – параллелограмм,
ВМ ⊥ (АВС), МС⊥DС
Определите вид параллелограмма АВСD
Слайд 7
5.
АВСD – параллелограмм, СМ⊥(АВС), МО ⊥ ВD
Определите вид
параллелограмма DАВС
6.
В ΔАВС ∠ С = 90º, О- центр
описанной окружности, АМ = МС, ОD⊥(АВС), АВ= 5, АС= 3Найдите DM
Слайд 8
№149
Дано: АD⊥(АВС), Δ АВС- равнобедренный,
АВ=АС= 5см, ВС
= 6 см, АD = 12 см.
Найти: ρ (А,
ВС), ρ (D, ВС)Решение:
1) Δ АВС- равнобедренный, АМ – медиана и высота → ρ (А, ВС) = АМ =
=4(см)
2) АМ – проекция, DМ - наклонная, АМ⊥BC → DМ⊥BC → ρ (D, ВС) = DМ =
Ответ: 4 см, 4√10 см.
Слайд 9
№ 150
Дано: АВСD - прямоугольник, АК⊥(АВС), КD =6
см, КВ= 7 см, КС= 9 см.
Найти: ρ (К,
(АВС)), ρ (АК, СD)Решение:
1). ρ (К, (АВС))= АК.
АК ⊥(АВС), АВ⊥CB, АВ – проекция, КВ – наклонная → КВ⊥ СВ.
2) ΔKBC – прямоугольный. СВ = 4√2(см) =АD
3) ΔAKD – прямоугольный. АК = 2 см.
4) ρ (АК, СD) = АD. AD = 4√2 см
Слайд 10
№159
Плоскости (АDМ) и (ВСМ) имеют общую
точку М, следовательно, они пересекаются по прямой, проходящей через
эту точку – МХ. Прямая АD, принадлежащая плоскости АDМ, параллельна прямой ВС, принадлежащей плоскости ВСМ,→ АD|| (ВСМ). А если плоскость проходит через прямую, параллельную другой плоскости и пересекает её, то линия пересечения плоскостей параллельна первой прямой→ МХ || AD. ВС||AD→MX||BC, но ВС⊥(АМВ) (почему?)→МХ⊥(АВМ)





























