Слайд 2
Текстовые задачи условно можно разбить на следующие основные
группы:
Задачи на производительность
задачи на работу
задачи на
бассейны и трубы
Задачи на проценты, концентрацию, части и доли
Задачи на проценты и доли
Задачи на концентрацию, смеси и сплавы
Слайд 3
Задачи на движение
по прямой (навстречу и вдогонку)
по замкнутой трассе
по воде
на среднюю скорость
протяженных
тел
Задачи на арифметическую и геометрическую прогрессии
Слайд 4
Алгоритм решения текстовых задач
Ввод переменных, т.е. обозначение
буквами x, y, z,... величины, которые требуется найти по
условию задачи.
Перевод условий задачи на язык математических соотношений, т.е. составление уравнений, неравенств, введение ограничения.
Решение уравнений или неравенств.
Проверка полученных решений на выполнение условий задачи.
Слайд 5
Указания к решению текстовых задач
Набор неизвестных должен
быть достаточным для перевода условий задачи на язык математических
соотношений. Как правило, за неизвестные следует принимать искомые величины.
Выбрав неизвестные, в процессе перевода условий задачи в уравнения или неравенства необходимо использовать все данные и условия задачи.
При составлении уравнений или неравенств необходимо исходить из требования о решении задачи в общем виде.
В составленных уравнениях надо проверить размерность членов уравнений
В процессе решения задачи, надо избегать результатов, противоречащих физическому смыслу.
Слайд 6
Задачи на проценты, концентрацию, части и доли
Слайд 8
Задача №1: Влажность свежескошенной травы 60%, сена
– 20%.
Сколько сена получится из 1 т свежескошенной
травы?
Решение: 1000 0,4 = 400 кг сухого вещества в траве
80 % - 400 кг
100 % - х кг
х = (100 400):80 = 500 кг
Ответ: 500 кг.
Вода
20 %
Вода
60 %
Сухое
вещество
80 %
Сухое
вещество
40 %
1 т
? кг
Слайд 9
Задача № 2: Яблоки подешевели на 20 %.
Сколько яблок можно
теперь купить на те же деньги,
на которые раньше покупали
2,8 кг яблок?
Слайд 10
Задача № 3: Арбуз весил 20 кг
и содержал 99 % воды, когда он немного усох,
то стал содержать 98 % воды. Сколько теперь весит арбуз?
Решение:
20 0,99 = 19,8 кг воды в арбузе
20 – 19,8 = 0,2 кг сухого вещества
После усыхания 100 98 = 2% - это 0,2 кг
0,2 : 0,02 = 10 кг
Ответ: 10 кг.
Слайд 11
Задача №4: В школьной столовой обед из двух
блюд стоит на 40 % дешевле, чем в кафе,
расположенном вблизи школы, причем «первое» стоит на 60%, а «второе» – на 30 % дешевле, чем в кафе. Во сколько раз в школьной столовой «второе» стоит дороже, чем «первое»?
Решение: пусть х цена «первого» в кафе, y цена «второго» в кафе, тогда
х+ y 0,4 (х +y) - стоимость в школьной столовой
0,4 х и 0,7 y – стоимость в школьной столовой отдельно каждого блюда
х+ y 0,4 (х +y) = 0,4 х + 0,7 y
0,6х +0,6 y = 0,4 x + 0,7 y
0,2х = 0,1 y
2x = y
х= 0,5y стоимость «первого» в кафе; 0,4 0,5 y = 0,2y стоимость «первого»
в столовой
0,7y : 0,2y = 3,5
то есть второе блюдо в столовой в 3,5 раза дороже
Ответ: 3,5
Слайд 12
Задача №5: В начале 2009 года мистер Джонс
приобрёл по 100 акций компаний А и В. Через
год он продал эти акции за сумму на 10 % большую той, что была заплачена им при покупке . При этом акции компании А были проданы на 5 % дороже, а акции компании В – на 20 % дороже, чем были им куплены. Во сколько раз акции компании В стоила дешевле акции компании А при их покупке мистером Джонсом?
Решение: пусть х цена одной акции А, y цена одной акции В
100 х+ 100 y цена купленных акций
100 х + 100 y +0,1 (100x + 100y) – цена акций через год
х + 0,05 х =1,05 х – цена одной акции А через год
y + 0,2y = 1, 2y – цена одной акции В через год
100 х + 100 y +0,1 (100x + 100y) = 100 1,05х + 100 1,2 y
110х + 110 y= 105 x +120 y
5x = 10y
x=2y
то есть акции компании А в 2 раза дороже акций компании В
Ответ: 2
Слайд 13
Задача №6: Изюм получается в процессе сушки винограда.
Сколько килограммов винограда потребуется для получения 6 килограммов изюма,
если виноград содержит 90 % воды, а изюм содержит 5 % воды.
Вода
90 %
Вода
5 %
Сухое
вещество
10 %
Сухое
вещество
95 %
6 кг
? кг
Решение: 6 0,95 = 5,7 кг сухого вещества в изюме, его количество не изменилось
5,7 кг – 10 %
х кг – 100 %
х = (5,7 100) : 10 = 57 кг изюма
Ответ : 57
Слайд 14
Задача №7: На аукционе одна картина была продана
с прибылью 20%, а другая – с прибылью 50%.
Общая прибыль от продажи двух картин составила 30%. У какой картины первоначальная стоимость была выше и во сколько раз?
Ответ: 2
Решение: пусть x стоимость первой картины, y – второй картины.
Прибыль от продажи первой 0,20х , второй – 0,50y.
Общая прибыль 0,30 (x + y)
0,20 х + 0,50y = 0,30 (x + y)
0,20x 0,30x = 0,30 y 0,50y
0,10x = 0,20y
Слайд 15
Задача №8: В четверг акции компании подорожали на
некоторое количество процентов, а пятницу подешевели на то же
самое количество процентов. В результате они стали стоить на 36 % дешевле, чем при открытии торгов в четверг. На сколько процентов подорожали акции компании в четверг?
1 + 0,01х – (1+0,01х)0,01х = 1 – 0,36
1 + 0,01х – 0,01х+0,0001х2 = 0,64
0,0001х2 = 0,36
х2 = 3600
х1 = 60
х2 = 60 не удов. условию задачи
Ответ: 60 %.
Решение:
Четверг – подорожали на х % 1 + 0,01х
Пятница – на столько же подешевели 1 + 0,01х – (1+0,01х)0,01х
Слайд 16
Задача №9: В кувшин налили 3 литра молока
8 % жирности, некоторое количество молока 2 % жирности
и тщательно перемешали. Определите сколько литров молока 2 % жирности было налито в кувшин, если известно, что жирность молока, полученного после перемешивания, составила 6 %?
Решение: Пусть х л молока – 2 % жирности
3 0,08 = 0,24 жира в 3 литрах 8 % молока
х 0,02 – жира в х литрах 2 % молока
0,24 + 0,02х = 0,06(3+ х)
0,24 + 0,02х = 0,18 + 0,06х
х = 1,5 л
Ответ: 1,5
Слайд 17
Задача №10: В апреле мобильный телефон стоил на
10 % больше, чем в июле, а в июле
он стоил на 15 % больше, чем в декабре. На сколько процентов стоимость телефона в апреле была выше, чем стоимость телефона в декабре?
Решение: пусть х цена в декабре
Апрель – 1,15 х+ 0,11,15х = 1,265х
Июль – 0,15 х + х = 1,15х
Декабрь – х
1,265х х = 0,265х разница в цене между апрелем и декабрем
х – 100 %
0,265 х – y %
y = (0,265х 100) : х = 26,5 %
Ответ: 26,5
Слайд 18
Задачи на концентрацию, смеси и сплавы
Слайд 19
Задача №1: В сосуд , содержащий 10 литров
15-процентного водного раствора некоторого вещества добавили 15 литров 10-процентного
водного раствора этого же вещества. Сколько процентов составит концентрация получившегося раствора?
+
=
Решение:
10 0,15 = 1,5 л вещества в
первом растворе
15 0,1 = 1,5 л вещества во 2 растворе
1,5 +1,5 = 3 л масса вещества в новом растворе
10 + 15 = 25 л масса нового раствора
25 л – 100 %
3 л – х %
х = 12 %
Ответ: 12
Слайд 20
Задача №2: В емкость содержащую 600 граммов 2
% раствора соли, добавили 1050 граммов воды, некоторое количество
соли и тщательно перемешали полученную смесь. Определите, сколько граммов соли было добавлено, если известно, что после перемешивания получился раствор, содержащий 2,5 % соли.
+
=
Решение: пусть х гр. соли добавили
600 0,02 = 12 гр. соли было в емкости
600 +1050 = 1650 гр. масса после добавления воды
1650 + х масса раствора после добавления соли
х +12 масса соли в новом растворе
(1650 + х) 0,025 = х + 12
41,25+ 0,025х = х + 12
х= 30 гр
Ответ: 30
+
Слайд 21
Задача №3: В двух бочках содержится сахарный сироп
различной концентрации. В первой бочке содержится 150 кг сиропа,
а во второй – 250 кг. Если перемешать весь сироп, находящийся в этих бочках, то получится сироп в котором 30 % сахара. А, если смешать равные массы сиропа из каждой бочки, то полученный сироп будет содержать 28 % сахара. Какова масса сахара в (кг), содержащегося в сиропе из второй бочки.
Решение: пусть х% сахара в первом сиропе, y % сахара во втором сиропе
150 + 250 = 400 кг масса нового сиропа
400 0,3 = 120 кг сахара в новом растворе
150 0,01 х + 250 0,01 y = 120
1 кг +1 кг = 2 кг – равные массы
0,01х + 0,01y = 0,28 2
x=20 % , y = 36 %
250 0,36 = 90 кг сахара во втором сиропе
Ответ: 90
+
=
Слайд 22
Задача №4: (ЕГЭ 05.06.14) Имеется два раствора .Первый
раствор содержит 10 % соли, второй – 30 %
соли. Из этих двух растворов получили третий раствор массой 200 кг, содержащий 25 % соли. На сколько килограммов масса первого раствора меньше массы второго раствора.
+
=
Решение: пусть х кг масса первого раствора,
y кг масса второго раствора
х + y = 200 кг масса нового раствора
200 0,25 = 50 кг соли в новом растворе
0,1х масса соли в первом растворе
0,3y масса соли во втором растворе
0,1х + 0,3y соли после смешивания в новом растворе т.е. 50 кг
Слайд 23
Задача №5:
Сколько граммов 30 %-го раствора надо добавить
к 80 г 12 %-го раствора этой же соли,
чтобы получить 20 %-й раствор соли?
Решение.
Пусть надо добавить х г 30 % раствора соли.
Получится (80 + х) г 20 % раствора.
В 80 г 12 % раствора содержится 800,12 г соли
0,3х г соли - в х г 30 % раствора,
0,2(80 + х) г соли - в (80 + х) г 20 % раствора.
Получаем уравнение:
0,3х + 0,1280 = 0,2(80 + х)
0,3 х + 9,6 =16 + 0,2х,
0,3 х 0,2 х = 16 – 9,6,
0,1 х = 6,4,
х = 64.
О т в е т: 64
Слайд 24
Задача №6: При смешивании первого раствора соли ,
концентрация которого 40 % ,и второго раствора этой же
соли, концентрация которого 48 %, получился раствор с концентрацией 42 %. В каком отношении взяты первый и второй растворы?
40 %
48 %
+
=
42 %
I – 40 % , х масса I , 0,40 х соли в I растворе
II 48 %, y масса II, 0,48y соли во II растворе
0,40х + 0,48 y = 0,42 (x + y)
0,40х + 0,42х = 0,42y + 0,48y
0,02х = 0,06y
х/y = 3/1
Ответ: 3 : 1.
Слайд 25
Задача №7: Сколько граммов воды надо добавить к
50 г раствора, содержащего 8 % соли, чтобы получить
5 % раствор?
Решение:
Пусть х - количество воды, которое надо добавить.
Новое количество раствора (50 + х) г.
Количество соли в исходном растворе 50 0,08 г.
Количество соли в новом растворе составляет 5 % от (50+ х) г,
т. е. 0,05(50+ х) г.
Так как количество соли от добавления воды не изменилось, то оно одинаково в исходном и новом растворах. Получаем уравнение. Иногда в химии это уравнение называют кратко «баланс по соли».
50 0,08 = 0,05(50+х),
508 = 5(50+х),
80 = 50 + х,
х = 30.
Ответ: 30
Слайд 26
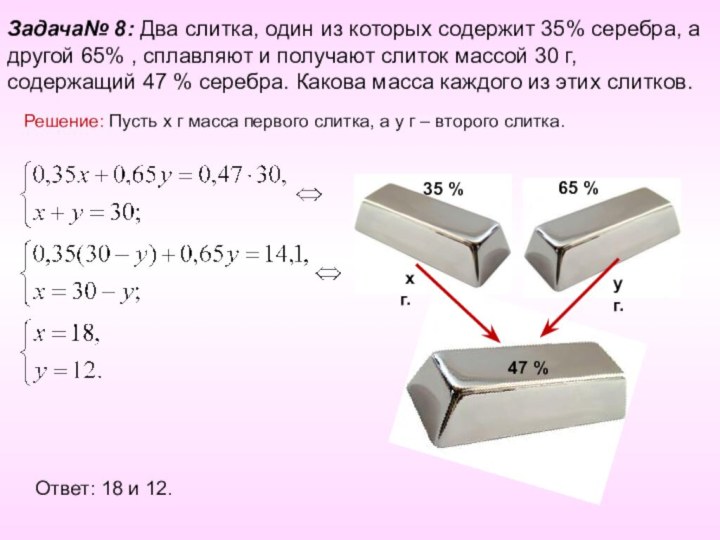
Задача№ 8: Два слитка, один из которых содержит
35% серебра, а другой 65% , сплавляют и получают
слиток массой 30 г, содержащий 47 % серебра. Какова масса каждого из этих слитков.
Решение: Пусть х г масса первого слитка, а y г – второго слитка.
35 %
65 %
x г.
y г.
47 %
Ответ: 18 и 12.
Слайд 27
Задача №9: Если смешать 8 кг и
2 кг растворов серной кислоты разной концентрации , то
получим 12 % раствор кислоты. При смешивании двух одинаковых масс тех же растворов получим 15 % раствор. Определите первоначальную концентрацию каждого раствора.
Решение: x % – концентрация в первом растворе,
y % концентрация во втором растворе
Ответ: 10 и 20.
Слайд 28
Задача №10: Имеются смеси апельсинового и ананасового
соков. Первая смесь содержит 40 % апельсинового сока, а
вторая – 80 %. Сливаются вместе p л первой смеси и q л второй смеси, а в результате получается 20 л смеси, содержащей 70 % апельсинового сока. Определите p и q.
p
q
40 %
80 %
20 л
70 %
Ответ: 5 и 15.
Слайд 30
Задачи на работу обычно содержат следующие
величины:
– время, в течение которого производится работа,
–
производительность труда, работа, произведенная в единицу времени (возможны и другие обозначения N, W);
– работа, произведенная за время t
Уравнения, связывающее эти три величины:
v
A
t
Слайд 31
В другой столбик
внесем
Урожай, собранный каждым звеном
Первый столбик
– урожайность.
Это условие поможет нам
составить уравнение.
х
х + 5
S, га
урожайность, ц/га
1. Одно звено собрало со своего участка 875 ц пшеницы,
а другое звено с участка, меньшего на 2 га, - 920 ц пшеницы. Сколько центнеров пшеницы собрало каждое звено с 1 га, если известно, что
с 1 га во втором звене собрали на 5 ц пшеницы больше, чем в первом?
1 способ
2 способ
3 способ
В новом столбике можно
выразить площадь участков,
для этого
весь урожай : урожайность
Это условие поможет ввести х …
Решив, любое из уравнений, мы сразу получим ответ на вопрос задачи, без дополнительных действий.
Слайд 32
Первый столбик – время, необходимое на выполнение работы
каждым насосом отдельно.
В другой столбик внесем выполненную работу –
это 1 часть
В новом столбике можно
выразить производительность (скорость) работы,
для этого
работу : время
х-2
х
2. При одновременной работе двух насосов пруд был очищен за
2 ч 55 мин. За сколько времени мог бы очистить пруд каждый насос, работая отдельно, если
один из них может эту работу выполнить на 2 ч быстрее другого?
справка
справка
справка
Это условие поможет ввести х …
A = 1
t =
= 1
Реши уравнение самостоятельно
Слайд 33
В новом столбике можно
выразить производительность (скорость) работы,
для
этого
работу : время
= 5
Первый столбик – время, необходимое
на выполнение работы каждой бригадой отдельно.
В другой столбик внесем выполненную работу – это 1 часть
х
х- 4
3. Одна из дорожных бригад может заасфальтировать некоторый участок дороги на 4 ч быстрее, чем другая. За сколько часов может заасфальтировать участок каждая бригада, если известно, что за 24 ч совместной работы они заасфальтировали 5 таких участков?
справка
справка
справка
Это условие поможет ввести х …
A = 5
t =
24
24
Реши уравнение самостоятельно
Слайд 34
В новом столбике можно
выразить производительность (скорость) работы,
для
этого
работу : время
Первый столбик – время, необходимое на
заполнение бассейна каждой трубе отдельно.
В другой столбик внесем выполненную работу –
это 1 часть
х
х- 5
4. Бассейн наполняется через первую трубу на 5 ч быстрее, чем через вторую. Бассейн можно наполнить, если открыть сначала первую трубу на 5 ч, а затем вторую на 7,5 ч. За сколько часов наполнится бассейн при совместной работе обеих труб?
справка
справка
Это условие поможет ввести х …
7,5
х
A1=
A2 =
1
5
= 1
= 1
+
Реши уравнение самостоятельно
Слайд 35
В новом столбике можно
выразить производительность (скорость) работы,
для
этого
работу : время
Первый столбик – время, необходимое на
выполнение всей работы каждой бригаде отдельно.
В другой столбик внесем выполненную работу –
это 1 часть
х
х- 12
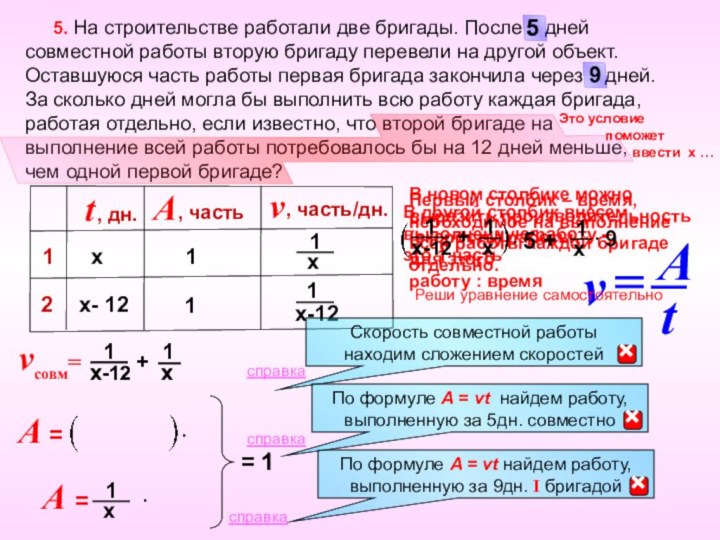
5. На строительстве работали две бригады. После 5 дней совместной работы вторую бригаду перевели на другой объект. Оставшуюся часть работы первая бригада закончила через 9 дней. За сколько дней могла бы выполнить всю работу каждая бригада, работая отдельно, если известно, что второй бригаде на выполнение всей работы потребовалось бы на 12 дней меньше, чем одной первой бригаде?
Это условие
поможет
ввести х …
= 1
= 1
5
справка
справка
справка
A =
A =
9
Реши уравнение самостоятельно
Слайд 36
Задача №6 : При одновременно работающих принтерах расход
бумаги составляет 1 пачку за 12 минут. Определите,
за сколько минут израсходует пачку первый принтер, если известно, что он сделает это на 10 минут быстрее, чем второй.
Слайд 37
Задача №7: Бассейн наполняется двумя трубами, действующими одновременно,
за 2 часа. За сколько часов может наполнить бассейн
первая труба, если она, действуя одна, наполняет бассейн на 3 часа быстрее, чем вторая?
Слайд 39
Задача №8: В городе имеются три завода по
выпуску рыбных консервов. Первый завод может переработать 50 тонн
рыбы за трое суток, второй – 45 тонн за двое суток, а третий – 95 тонн за шесть суток. Определите минимальное время, за которое на этих заводах можно переработать 110 тонн рыбы.
Слайд 40
Решение:
110 : 55 = 2 сут
Ответ: 2 суток.
Слайд 41
Задача №9: Первый наборщик текста набирает за час
5 страниц текста, второй – 6 страниц, а третий
– 7 страниц. Определите, по сколько страниц текста нужно отдать для набора каждому из них, если требуется, чтобы весь текст, объем которого 216 страниц, был набран как можно быстрее.
Решение:
5 + 6 + 7 = 18 частей всего
216 : 18 = 12 страниц 1 часть
12 5 = 60 стр.
12 6 = 72 стр.
12 7 = 84 стр.
Ответ: 60, 72, 84 страницы.
Слайд 43
Задачи на движение
по прямой (навстречу и вдогонку)
по замкнутой трассе
по воде
на среднюю скорость
протяженных
тел
Слайд 44
При решении задач на движение принимают такие допущения:
движение считается равномерным, если нет специальных оговорок;
изменение направления
движения и переходы на новый режим движения считаются происходящими мгновенно;
если два тела начинают движение одновременно (если одно тело догоняет другое), то в случае, если или встречаются, каждое тело с момента выхода и до встречи затрачивает одинаковое время;
Слайд 45
всякие переходы на новый режим движения, на новое
направление движения считают происходящим мгновенно;
если тела выходят в разное
время, то до момента встречи из них затрачивает время больше то, которое выходит раньше;
все величины, как правило, положительные (в природе скорость расстояние и время положительны), поэтому можно смело умножать, делить и возводить в квадрат получающиеся уравнения и неравенства, не делая необходимых в таких случаях оговорок.
Слайд 46
В задачах на движение используются обычно формулы, выражающие
законы равномерного движения: S=V·t , где S- пройденное расстояние,
V- скорость равномерного движения, t - время движения.
При составлении уравнений в таких задачах часто бывает удобно прибегнуть к геометрической иллюстрации процесса движения: путь изображается в виде отрезка прямой, место встречи движущихся с разных сторон объектов точкой на отрезке и т.д.
Часто для усложнения задачи её условие формулируется в различных единицах измерения(метры, километры, часы, минуты и т.д.). В этом случае при выписывании уравнений необходимо пересчитывать все данные задачи в одинаковых единицах измерения:
Слайд 47
Движение навстречу:
Движение вдогонку:
Движение по окружности
(замкнутой трассе):
Средняя скорость:
Слайд 48
Задачи на движение
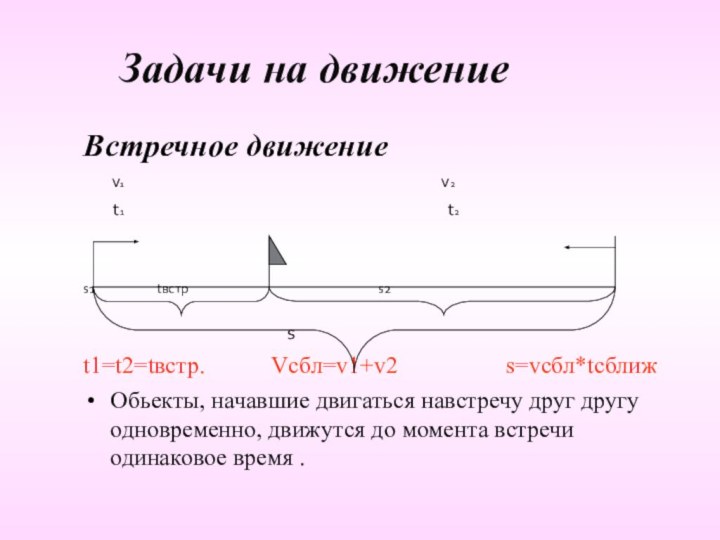
Встречное движение
v1
v2
t1 t2
s1 tвстр s2
s
t1=t2=tвстр. Vсбл=v1+v2 s=vсбл*tсближ
Обьекты, начавшие двигаться навстречу друг другу одновременно, движутся до момента встречи одинаковое время .
Слайд 49
Задача№ 1.Из городов A и B навстречу
друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в
B на 3 часа раньше, чем велосипедист приехал в A, а встретились они через 48 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
x – у = 3
Ответ: 4 ч
Слайд 50
Движение в одном направлении
v1
v2
t1 t2
s s2
s1 vсближ =v1-v2,.s=s1-s2 , s=vсбл*tвстр
Слайд 51
Задача№ 2: Первый велосипедист выехал из поселка
по шоссе со скоростью 15 км/ч. Через час после
него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
х – 10
х – 15
t
= 10
= 30
С системой придется потрудиться. При выборе ответа учтем, что скорость 3-го велосипедиста должна быть больше 15. Ответ: 25.
Слайд 52
Движение в противоположных направлениях
В таких задачах два тела
могут начинать движение в противоположных направлениях из одной точки:
а) одновременно;
б) в разное время.
А могут начинать свое движение из двух разных точек, находящихся на заданном расстоянии, и в разное время.
Общим теоретическим положением для них будет следующее:
v удал. = v1+ v2, где v1 и v2 соответственно скорости первого и второго тел.
(Схематический чертеж строится аналогично предыдущим).
Слайд 53
Задача№ 3. Велосипедист выехал с постоянной скоростью
из города А в город В, расстояние между которыми
равно 72 км. На следующий день он отправился обратно со скоростью на 6 км/ч больше прежней. По дороге он сделал остановку на 6 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Путь В-А
х
72
х+6
72
72 км
Это условие поможет ввести х …
6 км/ч
Слайд 54
Движение по воде
скорость перемещения лодки V по воде,
при скорости течения реки Vр и собственной скорости движения
Vс, выражается:
V по течению=Vс+Vр при движении лодки по течению реки.
V против течения=Vс−Vр при движении лодки против течения реки.
Движущийся плот всегда имеет скорость течения реки.
Слайд 55
Задача№ 4:Теплоход проходит по течению реки до
пункта назначения 560
км и после стоянки возвращается в пункт
отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 8 часов, а в пункт отправления теплоход возвращается через 56 часов после отплытия из него. Ответ дайте в км/ч.
х–4
560
Пусть vсоб. = x
справка
Это условие поможет ввести х …
справка
Ответ: 24
Слайд 57
Если два велосипедиста одновременно начинают движение по окружности
в одну сторону со скоростями v1 и v2 соответственно
(v1
> v2 соответственно), то 1-й велосипедист
приближается ко 2 со скоростью v1 – v2.
В момент, когда 1-й велосипедист
в первый раз догоняет 2-го,
он проходит расстояние на
один круг больше.
Продолжить
Показать
В момент, когда 1-й
велосипедист во
второй раз догоняет
2-го, он проходит
расстояние на два
круга больше и т.д.
Слайд 58
Задача№ 5: Из одной точки круговой трассы,
длина которой равна15 км, одновременно в одном направлении стартовали
два автомобиля. Скорость первого автомобиля равна 60 км/ч, скорость второго равна 80 км/ч. Сколько минут с момента старта пройдет, прежде чем первый автомобиль будет опережать второй ровно на 1 круг?
Ответ: 45
х получим в часах.
Не забудь перевести в минуты.
Показать
Слайд 59
Задача№6: Из одной точки круговой трассы, длина
которой равна 10 км, одновременно в одном направлении стартовали
два автомобиля.
Скорость первого автомобиля равна 90 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Ответ: 75
Показать
Слайд 60
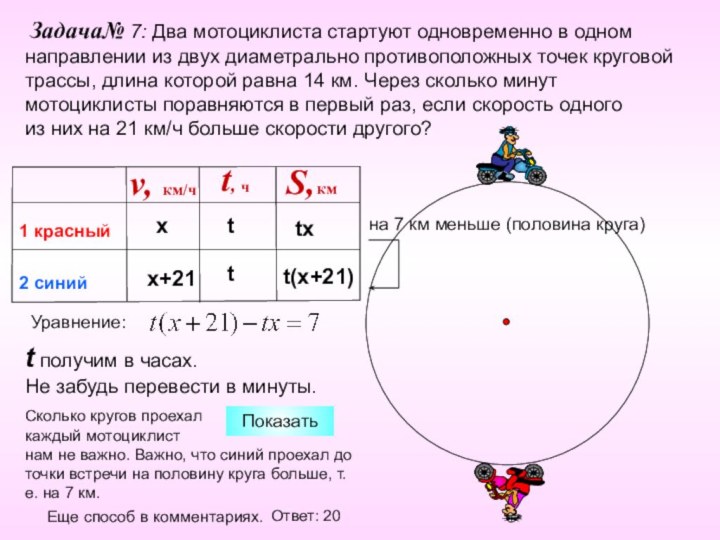
Задача№ 7: Два мотоциклиста стартуют одновременно в
одном направлении из двух диаметрально противоположных точек круговой трассы,
длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного
из них на 21 км/ч больше скорости другого?
Ответ: 20
t получим в часах.
Не забудь перевести в минуты.
Сколько кругов проехал
каждый мотоциклист
нам не важно. Важно, что синий проехал до точки встречи на половину круга больше, т.е. на 7 км.
Еще способ в комментариях.
Показать
Слайд 61
Пусть полный круг – 1 часть.
Задача№
8: Лыжные соревнования проходят на круговой лыжне. Первый лыжник
проходит один круг на 2 минуты быстрее второго и через час опережает второго ровно на один круг. За сколько минут второй лыжник проходит один круг?
Показать
Слайд 62
Задача№ 9. Лыжные соревнования проходят на круговой
лыжне. Первый лыжник проходит один круг на 2 минуты
быстрее второго и через час опережает второго ровно на один круг. За сколько минут второй лыжник проходит один круг?
Ответ: 10
х
х+2
Сначала выразим скорость каждого лыжника. Пусть за х мин 1-й лыжник проходит полный круг. Второй на 2 минуты больше, т.е. х+2.
Это условие поможет ввести х …
Слайд 63
Задача№ 10: Из одной точки круговой трассы,
длина которой равна 14 км, одновременно в одном направлении
стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Можно было сначала найти скорость вдогонку: 80 – х
Тогда уравнение будет выглядеть так:
Ответ: 59
Нажать на кнопку можно несколько раз. Сколько кругов проехал каждый автомобиль нам
не важно. Важно, что желтый автомобиль проехал на 1 круг больше, т.е. на 14 км.
Показать
Слайд 64
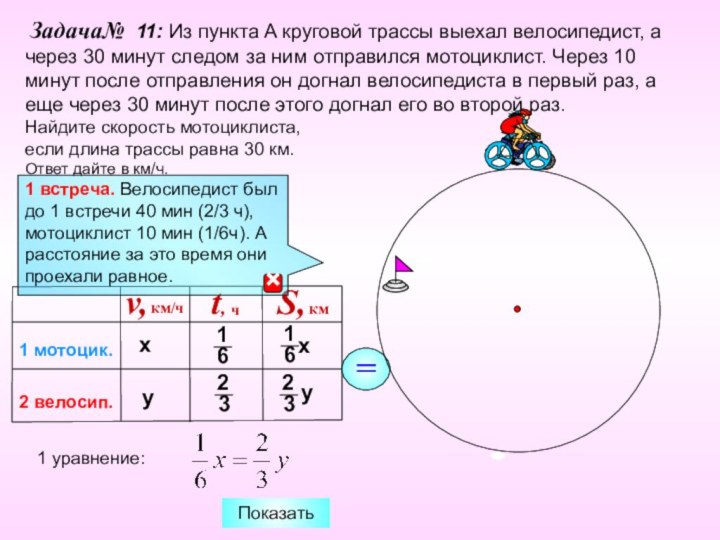
Задача№ 11: Из пункта A круговой трассы
выехал велосипедист, а через 30 минут следом за ним
отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз.
Найдите скорость мотоциклиста,
если длина трассы равна 30 км.
Ответ дайте в км/ч.
Показать
Слайд 65
Задача №12. Из пункта A круговой
трассы выехал велосипедист, а через 30 минут следом за
ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км.
Ответ дайте в км/ч.
Ответ 80
Искомая величина – х
Показать (2)
Слайд 66
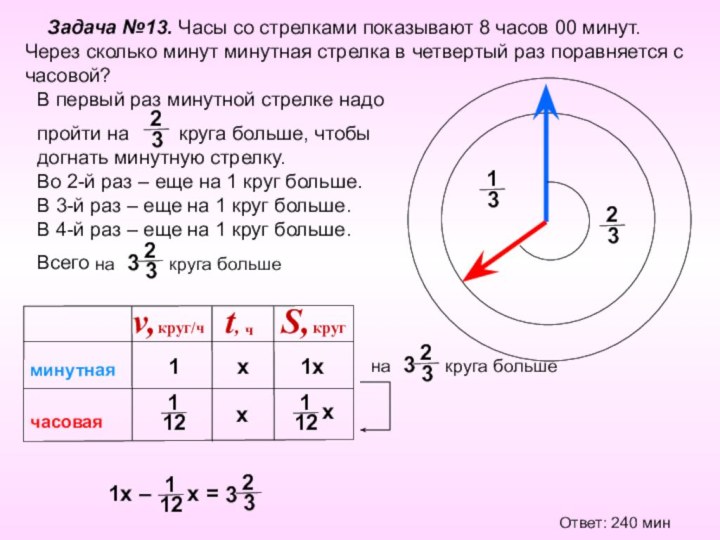
Задача №13. Часы со стрелками показывают
8 часов 00 минут. Через сколько минут минутная стрелка
в четвертый раз поравняется с часовой?
х
1
х
1х
Ответ: 240 мин
Слайд 67
6
12
1
2
9
11
10
8
7
4
5
3
Показать (4)
Проверка
Другой способ – в комментариях.
Слайд 68
Задачи на движение протяженных тел
В задачах на движение
протяжных тел требуется определить длину одного из них. Наиболее
типичные ситуации: определение длины поезда проезжающего мимо
придорожного столба
идущего параллельно путям пешехода
лесополосы определенной длины
другого двигающегося поезда
Если поезд движется мимо столба, то он проходит расстояние равное его длине. Если поезд движется мимо протяженной лесополосы, то он проходит расстояние равное сумме длины самого поезда и лесополосы.
Слайд 69
Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает
мимо придорожного столба за 36 секунд. Найдите длину поезда
в метрах.
Пройденное расстояние = длине поезда
Выразим время в часах
Задача № 1
Слайд 70
Задача № 2 Поезд, двигаясь равномерно со
скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна
400 метрам, за 1 минуту. Найдите длину поезда в метрах.
400 м
Пройденное расстояние = длине поезда + длина лесополосы
Решение. Зная скорость движения v = 60 км/ч и время, за которое он проезжает мимо лесополосы t = 1 мин, можно найти расстояние, которое прошел поезд (длина лесополосы + длина поезда).
Выразим время в часах
Слайд 71
Задача № 3 Поезд, двигаясь равномерно со скоростью
60 км/ч, проезжает мимо лесополосы, длина которой равна 400
метрам, за 1 минуту. Найдите длину поезда в метрах.
400 м
Решим задачу с помощью уравнения
x
Слайд 72
При решении задач на движение
двух тел часто очень
удобно считать одно тело неподвижным, а
другое — приближающимся к нему со скоростью, равной сумме скоростей
этих тел (при движении навстречу) или разности скоростей
(при движении вдогонку). Такая модель помогает разобраться
с условием задачи.
Задача № 4 По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
Воспользуемся предложенной моделью
Слайд 73
По морю параллельными курсами в одном направлении следуют
два сухогруза: первый длиной 120 метров, второй — длиной 80
метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
Решение. Будем считать, что первый сухогруз неподвижен, а второй приближается к нему со скоростью v (м/мин) , равной разности скоростей второго и первого сухогрузов. Тогда за 12 минут второй сухогруз проходит расстояние
1200 м
Слайд 74
Задача № 6 По двум параллельным железнодорожным путям
в одном направлении следуют пассажирский и товарный поезда, скорости
которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.
600 м
Скорость вдогонку (на сколько скорость пассажирского поезда больше скорости товарного)
Слайд 75
Задача № 7 По двум параллельным железнодорожным путям
в одном направлении следуют пассажирский и товарный поезда, скорости
которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.
600 м
Решим задачу с помощью уравнения
x
Слайд 76
Задача № 8 По двум параллельным железнодорожным
путям друг навстречу другу следуют скорый и пассажирский поезда,
скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.
700 м
Скорость навстречу друг другу
(сумма скоростей при движении навстречу друг другу)
Слайд 77
Задача № 9 По двум параллельным железнодорожным путям
друг навстречу другу следуют скорый и пассажирский поезда, скорости
которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.
700 м
Решим задачу с помощью уравнения
x
Слайд 78
Задача № 10 Поезд, двигаясь равномерно со
скоростью 54 км/ч, проезжает
мимо идущего параллельно путям со скоростью
6 км/ч
навстречу ему пешехода за 30 секунд. Найдите длину поезда
в метрах.
Выразим время в минутах
Решение. Будем считать, что пешеход неподвижен, а поезд двигается со скоростью v (м/мин), равной сумме скоростей пешехода и поезда (скорость навстречу друг другу). Сам пешеход не имеет «протяженной» длины (если бы это была колонна солдат, то мы бы учли это).
Скорость навстречу друг другу (сумма скоростей при движении навстречу друг другу)
Слайд 79
Задача № 11 Поезд, двигаясь равномерно со скоростью
65 км/ч, проезжает
мимо идущего в том же направлении параллельно
путям
со скоростью 5 км/ч пешехода за 30 секунд. Найдите
длину поезда в метрах.
Выразим время в минутах
Решение. Будем считать, что пешеход неподвижен, а поезд двигается со скоростью v (м/мин), равной разности скоростей пешехода и поезда. Пешеход не имеет «протяженной» длины.
Скорость навстречу друг другу (сумма скоростей при движении навстречу друг другу)
Слайд 80
Чтобы определить среднюю скорость при неравномерном движении, надо
весь пройденный путь разделить на все время движения:
Задачи на
нахождение
средней скорости
Слайд 82
Задача №12: Автомобиль двигался 3,2ч по шоссе
со скоростью 90км/ч, затем 1,5ч по грунтовой дороге со
скоростью 45км/ч, наконец, 0,3ч по проселочной дороге со скоростью 30км/ч. Какова средняя скорость движения автомобиля на всем пути?
Средняя скорость движения определяется по формуле: