Д. Пойа
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему К уроку математики в 11 классе. Подготовка к ЕГЭ. Решение текстовых задач.
Содержание
- 2. Текстовые задачи
- 3. Текстовые задачи в различных учебниках алгебры 9 класса
- 4. Поиск пути решения задачи и составление плана
- 5. Текстовые задачи:Задачи на движение.Задачи на работу.Задачи на сплавы и смеси. Задачи на проценты.
- 6. 1. Задачи на движение.
- 7. 1.1 Движение навстречу1. Расстояние между городами А
- 8. Задачи на движение.Х км/ч60 км/ч660км34+3
- 9. 1.1. Движение навстречу420 + 3х = 660
- 10. 1.1. Движение навстречу2. Два автомобиля выезжают навстречу
- 11. 1.1. Движение навстречу2. Два автомобиля выезжают навстречу
- 12. 1.2. Движение вдогонку1. Два пешехода отправляются одновременно
- 13. 1. Два пешехода отправляются одновременно из одного
- 14. 1.2. Движение вдогонку№ 26578
- 16. 1.3.Движение с задержкой1. Поезд вышел со станции
- 17. 1. Поезд вышел со станции А по
- 18. 1.4. Движение по окружности
- 19. 1. Из одной точки круговой трассы, длина
- 20. 1.5. Движение по воде 1.
- 21. 1. Моторная лодка прошла 80 км от
- 22. 1.5. Движение по воде2. Теплоход плывёт из
- 23. 1.6. Задачи на среднюю скорость
- 24. 1. Первую треть трассы велосипедист ехал со
- 25. 1.7. Задачи на движение протяжённых тел1. По
- 26. 1. По морю параллельными курсами в одном
- 27. 2. Задачи на работу А = рt, из
- 28. 2. Ключевая задача на работу
- 29. 2.1. Задачи на работу1. Каждый из двух
- 30. 1. Каждый из двух рабочих одинаковой квалификации
- 31. 3. Задачи на смеси и сплавы3.1. Найдите
- 32. 3. Задачи на смеси и сплавы3.2. Виноград
- 33. 3. Задачи на смеси и сплавы3.3. Смешав
- 34. 4. Задачи на проценты. 1. Пять рубашек
- 35. Сложности при решении текстовых задачсоставление математической моделисоставление
- 36. Сложности при решении текстовых задач и
- 37. Сложности при решении текстовых задач и
- 38. Сложности при решении текстовых задач и
- 39. Сложности при решении текстовых задач и
- 40. ВыводыДля того, чтобы научиться решать задачи, надо
- 41. Скачать презентацию
- 42. Похожие презентации






































Слайд 2
Текстовые задачи
«Умение решать задачи – практически искусство, подобно плаванию, или катанию на коньках, или игре на фортепиано: научиться этому можно, лишь подражая избранным образцам и постоянно тренируясь»
Д. Пойа
Слайд 4
Поиск пути решения задачи и составление плана решения
Анализ
по тексту
Аналитический путь решения задачи (от вопроса к данным)
Синтетический
путь решения задачи (от данных к вопросу)Комбинированный путь (анализ и синтез)
Разбиение задачи на смысловые части
Введение подходящих обозначений
Слайд 5
Текстовые задачи:
Задачи на движение.
Задачи на работу.
Задачи на сплавы
и смеси.
Задачи на проценты.
Слайд 6
1. Задачи на движение.
1.1 Движение по прямой:
1.1. навстречу.1.2. вдогонку.
1.3. с задержкой.
1.4. Движение по окружности.
1.5. Движение по воде.
1.6. Задачи на среднюю скорость.
1.7. Задачи на движение протяжённых тел.
Слайд 7
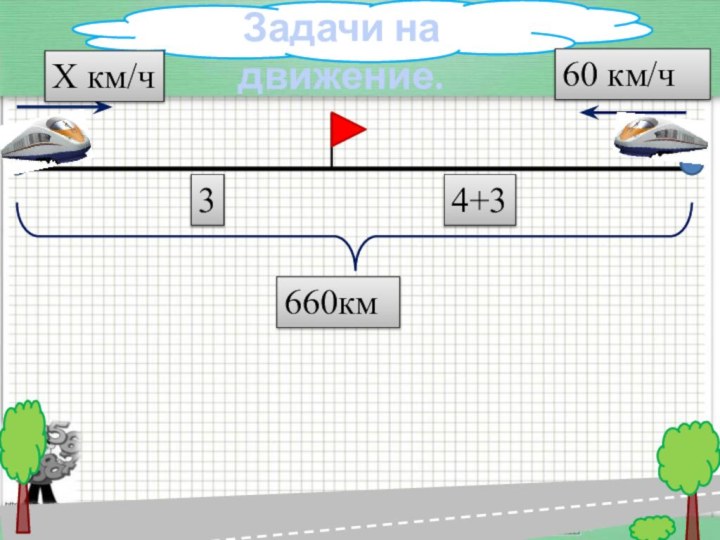
1.1 Движение навстречу
1. Расстояние между городами А и
Б равно 660 км. Из города А в город
Б со скоростью 60 км/ч выехал поезд, а через 4 часа после этого навстречу ему из города Б выехал второй поезд. Найдите скорость второго поезда, если поезда встретились через 3 часа после его выезда из города Б. Ответ дайте в км/ч.
Слайд 9
1.1. Движение навстречу
420 + 3х = 660
1. 660 – 420 = 240 (км)
3х = 660 – 420 2. 240 : 3 = 80 (км/ч)
3х = 240
Х= 80 (км/ч)
Ответ 80 км/ч
Слайд 10
1.1. Движение навстречу
2. Два автомобиля выезжают навстречу друг
другу их двух пунктов, расстояние между которыми 400 км.
Если первый выедет на 5 часов раньше второго, то они встретятся через 5 часов после выезда второго. Если второй выедет на 2 часа раньше первого, то он встретит первого через 6 часов после своего выезда.Найдите скорости автомобилей.
Слайд 11
1.1. Движение навстречу
2. Два автомобиля выезжают навстречу друг
другу их двух пунктов, расстояние между которыми 400 км.
Если первый выедет на 5 часов раньше второго, то они встретятся через 5 часов после выезда второго. Если второй выедет на 2 часа раньше первого, то он встретит первого через 6 часов после своего выезда. Найдите скорости автомобилейОтвет: 10км/ч и 60 км/ч
Слайд 12
1.2. Движение вдогонку
1. Два пешехода отправляются одновременно из
одного и того же места на прогулку по алее
парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300м?Слайд 13 1. Два пешехода отправляются одновременно из одного и
того же места на прогулку по алее парка. Скорость
первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300м?
Слайд 14
1.2. Движение вдогонку
№ 26578 Из
пункта A в пункт B одновременно выехали два автомобиля.
Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути — со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первогоавтомобиля. Ответ дайте в км/ч.
Слайд 15
Ответ: 32 км/ч
№ 26578 Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути — со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч
Слайд 16
1.3.Движение с задержкой
1. Поезд вышел со станции А
по направлению к станции В. Пройдя 420 км, что
составляет 60% всего пути АВ, поезд остановился из-за снежного заноса. Через полчаса путь был расчищен, и машинист, увеличив скорость на 10 км/ч привёл его на станцию В без опоздания. Найдите скорость поезда, с которой он прибыл на станцию В.Слайд 17 1. Поезд вышел со станции А по направлению
к станции В. Пройдя 420 км, что составляет 60%
всего пути АВ, поезд остановился из-за снежного заноса. Через полчаса путь был расчищен, и машинист, увеличив скорость на 10 км/ч привёл его на станцию В без опоздания. Найдите скорость поезда, с которой он прибыл на станцию В.
Ответ: 80 км/ч
Слайд 18
1.4. Движение по окружности
1.
Из одной точки круговой трассы, длина которой 14 км,
одновременно в одном направлении стартовали два автомобилиста. Скорость первого равна 80км/ч, и через 40 минут после старта он опережал второго автомобилиста ровно на один круг. Найдите скорость второго автомобилиста. Ответ дайте в км/ч.Слайд 19 1. Из одной точки круговой трассы, длина которой
14 км, одновременно в одном направлении стартовали два автомобилиста.
Скорость первого равна 80км/ч, и через 40 минут после старта он опережал второго автомобилиста ровно на один круг. Найдите скорость второго автомобилиста. Ответ дайте в км/ч
Слайд 20
1.5. Движение по воде
1. Моторная
лодка прошла 80 км от пункта А до пункта
В и после трёхчасовой стоянки вернулась обратно, затратив на весь путь 12 часов .Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.Слайд 21 1. Моторная лодка прошла 80 км от пункта
А до пункта В и после трёхчасовой стоянки вернулась
обратно, затратив на весь путь 12 часов .Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.Пусть х км/ч – скорость лодки в неподвижной воде
Слайд 22
1.5. Движение по воде
2. Теплоход плывёт из А
в В двое суток, из В в А трое
суток. Сколько суток плывет из А в В плот?Решение:
если S – путь из А в В
х – собственная скорость теплохода
у – скорость течения реки,
то время движения плота равно S/у
Т.к. S = (х+у)·2 и S = (х-у)·3
составим уравнение: 2х+2у = 3х-3у
-х = -5у; х = 5у
Значит S = 2х+2у = 2·5у+2у = 12у
Тогда S/у = 12у : у = 12
Ответ: 12 суток
Слайд 23
1.6. Задачи на среднюю скорость
1.
Первую треть трассы велосипедист ехал со скоростью 12км/ч, вторую
треть – со скоростью-16км/ч, а последнюю треть – со скоростью24км/ч. Найдите среднюю скорость велосипедиста на протяжении всего пути. Ответ дайте в км/ч.Слайд 24 1. Первую треть трассы велосипедист ехал со скоростью
12км/ч, вторую треть – со скоростью-16км/ч, а последнюю треть
– со скоростью24км/ч. Найдите среднюю скорость велосипедиста на протяжении всего пути. Ответ дайте в км/ч.
Слайд 25
1.7. Задачи на движение протяжённых тел
1. По морю
параллельными курсами в одном направлении следуют два сухогруза: первый
длиной 120м, второй длиной 80м. Второй сухогруз отстаёт от первого на 400 м, но уже через 12 минут опережает первый на 600м. На сколько километров в час скорость первого сухогруза меньше скорости второго?Ё1ЁЁЁЁЁЁЁЁЁЁЁЁЁЁЁЁЁЁ
Слайд 26 1. По морю параллельными курсами в одном направлении
следуют два сухогруза: первый длиной 120м, второй длиной 80м.
Второй сухогруз отстаёт от первого на 400 м, но уже через 12 минут опережает первый на 600м. На сколько километров в час скорость первого сухогруза меньше скорости второго?
Слайд 27
2. Задачи на работу
А = рt, из этой
формулы легко найти р (производительность) или t.
Если объем работы не важен и нет никаких данных, позволяющих его найти – работу принимаем за единицу.Если трудятся два рабочих (два экскаватора и т.д.) – их производительности складываются.
В качестве переменной удобно взять производительность
Слайд 29
2.1. Задачи на работу
1. Каждый из двух рабочих
одинаковой квалификации может выполнить заказ за 15 часов. Через
3 часа после того, как один их них приступил к выполнению заказа. К нему присоединился другой рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?Слайд 30 1. Каждый из двух рабочих одинаковой квалификации может
выполнить заказ за 15 часов. Через 3 часа после
того, как один их них приступил к выполнению заказа. К нему присоединился другой рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?
Слайд 31
3. Задачи на смеси и сплавы
3.1. Найдите концентрацию
кислоты, полученной при смешивании 30кг её 80% и 20кг
её 60% растворов. Ответ выразите в процентах.Ответ: 72%
Слайд 32
3. Задачи на смеси и сплавы
3.2. Виноград содержит
91% влаги, а изюм- 7%. Сколько килограммов винограда потребуется
для получения 21кг изюма?Ответ: 217кг
Слайд 33
3. Задачи на смеси и сплавы
3.3. Смешав 30%
и 60% растворы кислоты и добавив 10кг чистой воды,
получили 36% раствор этой кислоты. Если бы вместо 10кг воды добавили 10кг 50% раствора той же кислоты, то получили 41% раствор кислоты. Сколько кг 30% раствора использовали для получения смеси?Ответ: 60кг
Слайд 34
4. Задачи на проценты.
1. Пять рубашек дешевле
куртки на 25%. На сколько процентов семь рубашек дороже
куртки?Решение:
Обозначим через х-стоимость одной рубашки, через у- стоимость одной куртки. Из условия задачи следует, что
5х=0,75у. Откуда х=0,15у. Тогда 7х=0,15у 7=1,05у.
Значит стоимость рубашки больше стоимости куртки на 5 сотых, т.е. семь рубашек дороже куртки на 5%
Ответ: 5%
Слайд 35
Сложности при решении
текстовых задач
составление математической модели
составление уравнений
и неравенств,
связывающих данные величины и переменные,
которые вводят
учащиеся нахождение соответствия между различными
величинами, применительно к которым формулируется
вопрос задачи
решение уравнений, системы уравнений
или неравенств
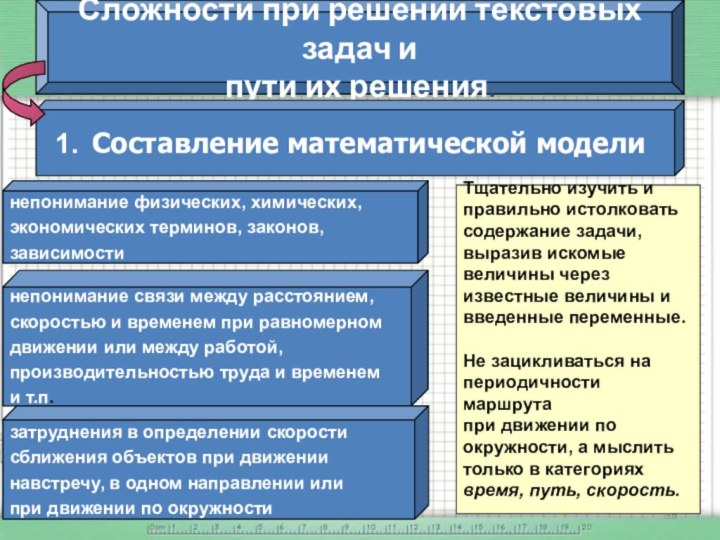
Слайд 36 Сложности при решении текстовых задач и пути их
решения.
Составление математической модели
непонимание физических, химических,
экономических терминов, законов,
зависимости
непонимание связи между расстоянием,
скоростью и временем при равномерном
движении или между работой,
производительностью труда и временем
и т.п.
затруднения в определении скорости
сближения объектов при движении
навстречу, в одном направлении или
при движении по окружности
Тщательно изучить и
правильно истолковать
содержание задачи,
выразив искомые
величины через
известные величины и
введенные переменные.
Не зацикливаться на
периодичности маршрута
при движении по
окружности, а мыслить
только в категориях
время, путь, скорость.
Слайд 37 Сложности при решении текстовых задач и пути их
решения.
2. Составление уравнений и неравенств, связывающих
данные величины и
переменные, которые вводят учащиесянеправильный выбор величин,
относительно которых составляется
уравнение
усложнение процесса составления
уравнения из-за неправильного
выбора величин
Важно правильно
выбрать величины,
относительно
которых будет
составлено уравнение.
Неправильный выбор
делает процесс
составления уравнения
более сложным.
Слайд 38 Сложности при решении текстовых задач и пути их
решения.
3. Нахождение соответствия между различными
величинами,
применительно к которым формулируется вопрос задачи
невозможность нахождения значения
переменных, которые в уравнениях
присутствуют и не являются
необходимыми
большое количество неизвестных,
нахождение значения которых
не являются необходимыми
Держать в поле зрения
основную цель, не боясь
вводить столько
вспомогательных
переменных, сколько их
понадобится по ходу
решения.
Совсем необязательно
ставить в качестве
непременного условия
сведение числа
неизвестных к
минимуму.
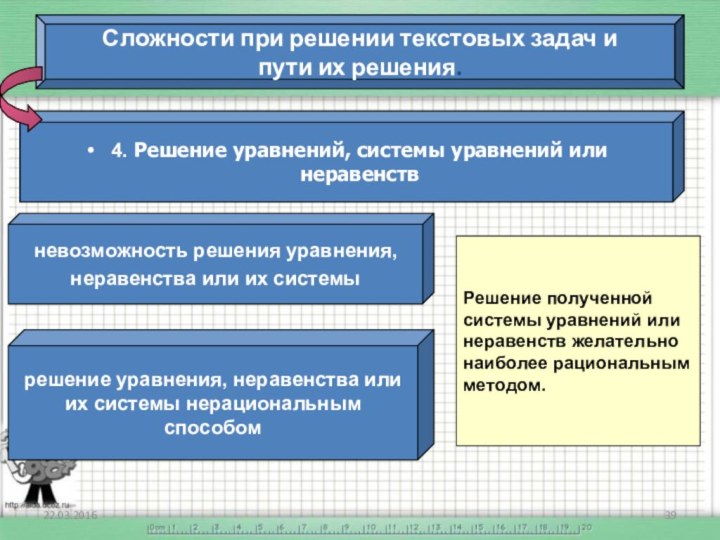
Слайд 39 Сложности при решении текстовых задач и пути их
решения.
4. Решение уравнений, системы уравнений или неравенств
невозможность решения
уравнения, неравенства или их системы
решение уравнения, неравенства или
их системы нерациональным способом
Решение полученной
системы уравнений или
неравенств желательно
наиболее рациональным
методом.
Слайд 40
Выводы
Для того, чтобы научиться решать задачи, надо приобрести
опыт их решения путем многократного повторения операций, действий, составляющих
предмет изучения.Редкие ученики самостоятельно приобретают такой опыт. Долг учителя - помочь учащимся приобрести опыт решения задач, научить их решать задачи.
Помощь учителя не должна быть чрезмерной, но и не быть слишком малой
Навыки решения текстовых задач формируются на основе осмысленных знаний и умений
Для формирования навыков нужна тщательно продуманная система упражнений и задач «от простого к сложному».
Знания учащихся по математике должны совершенствоваться с решением каждой новой задачи
Следует добиваться, чтобы осознанные умения и навыки ученики
получали при наименьших затратах времени.
Следует учитывать индивидуальные особенности и возможности
учащихся.