by
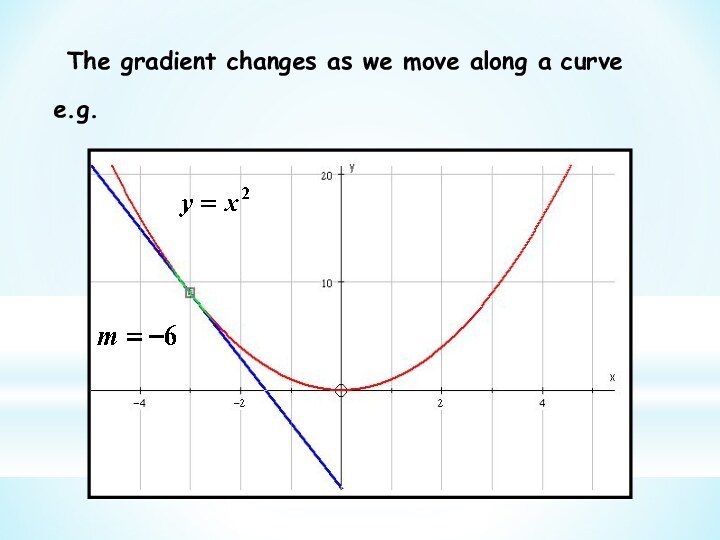
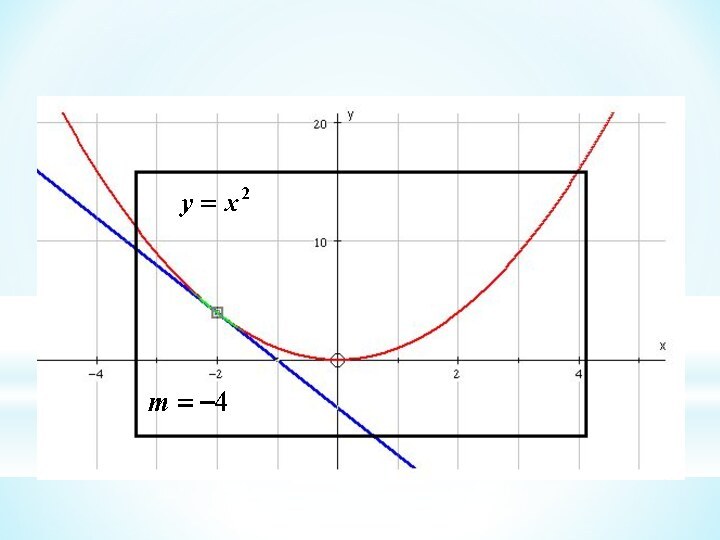
We use this idea to get the gradient at
a point on a curve This branch of Mathematics is called Calculus
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


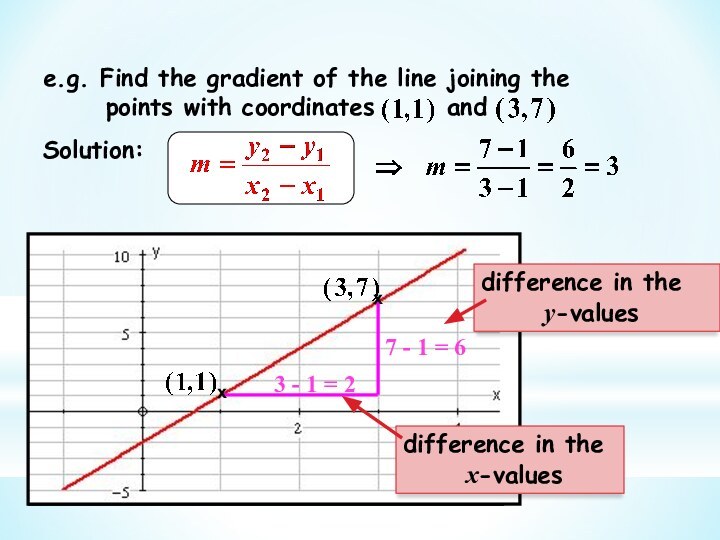

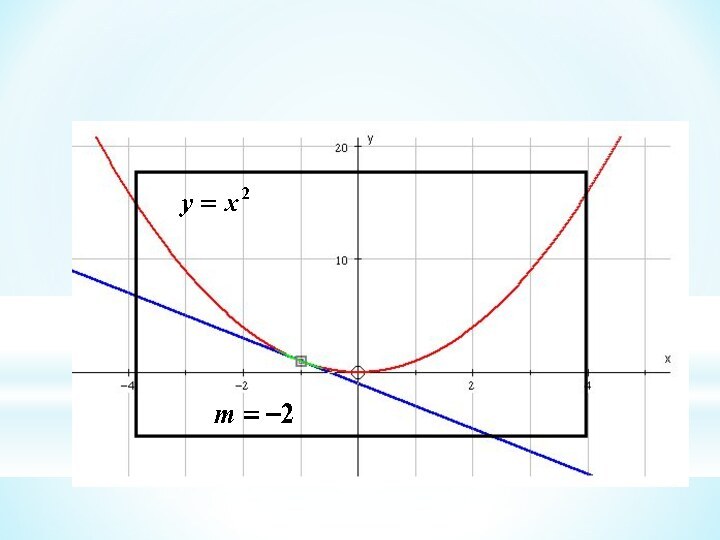
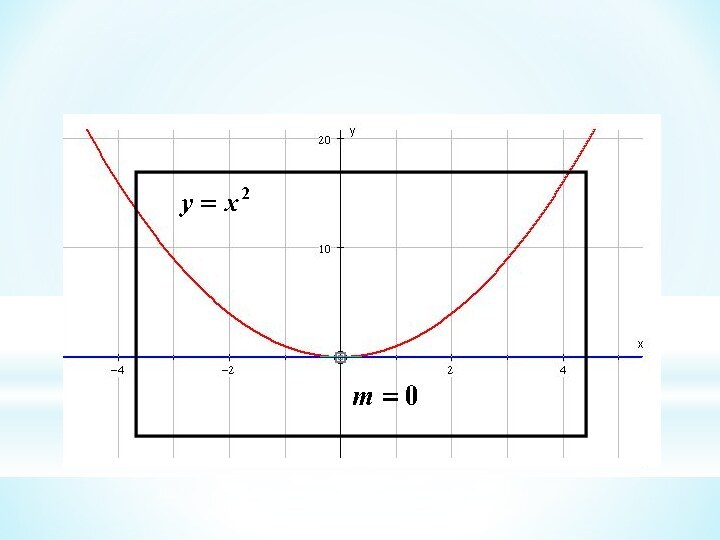

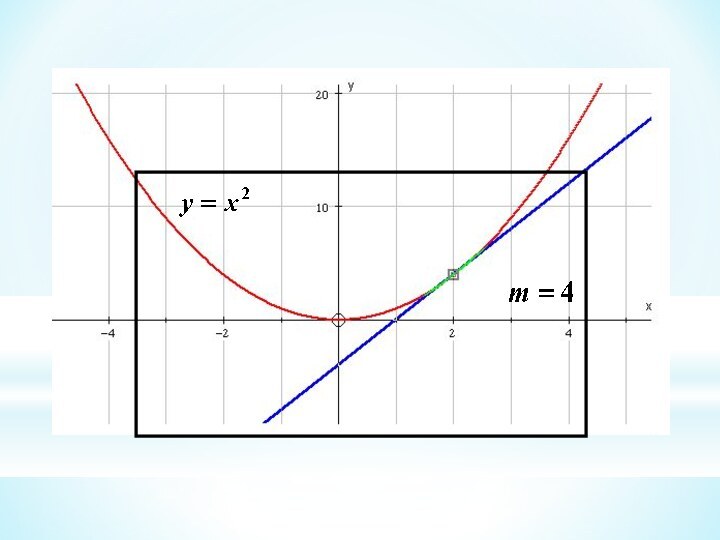
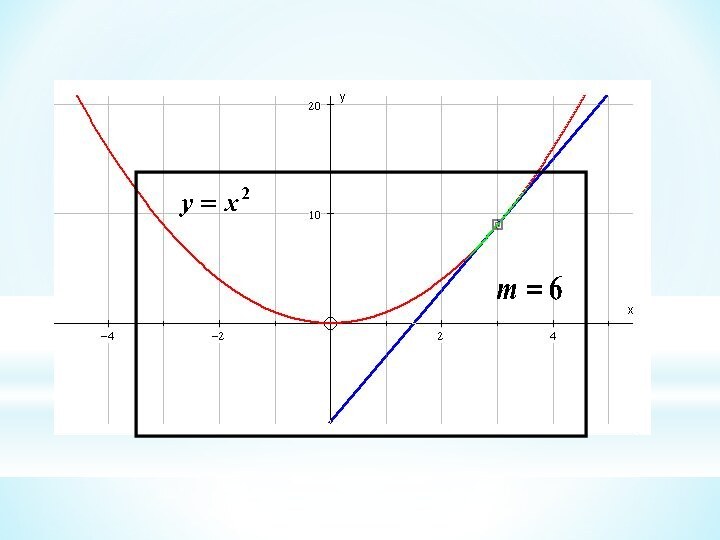






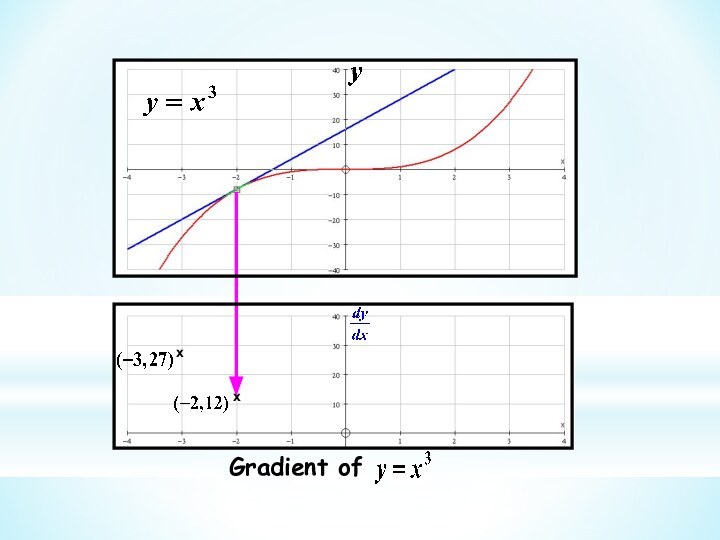
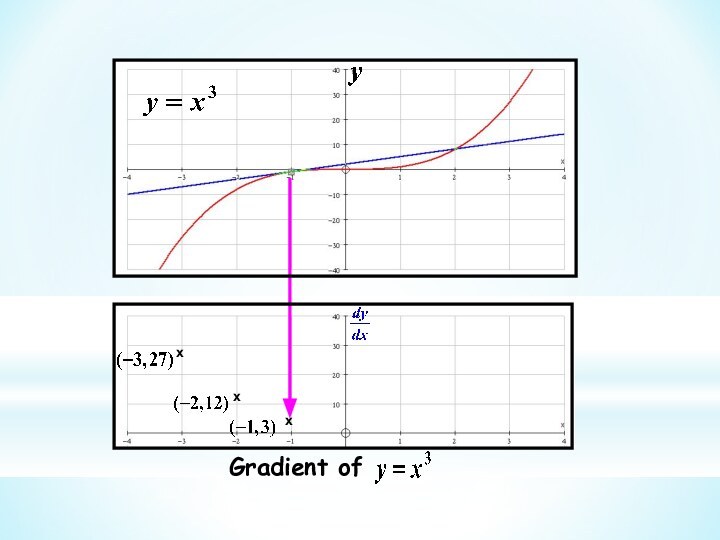
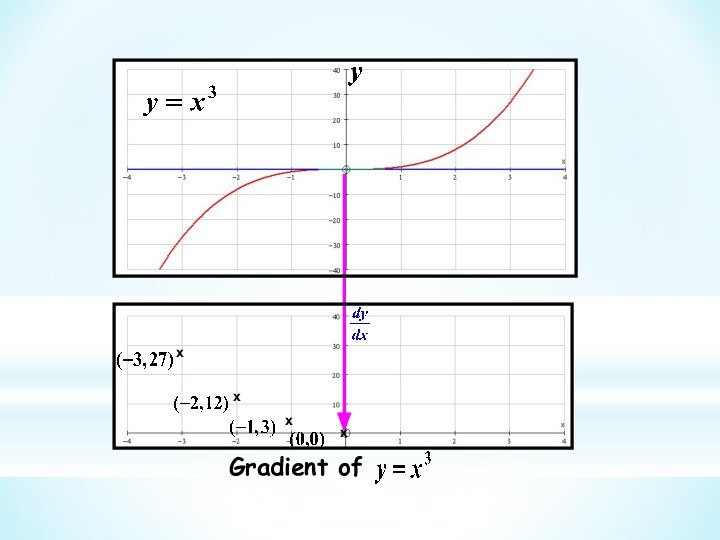

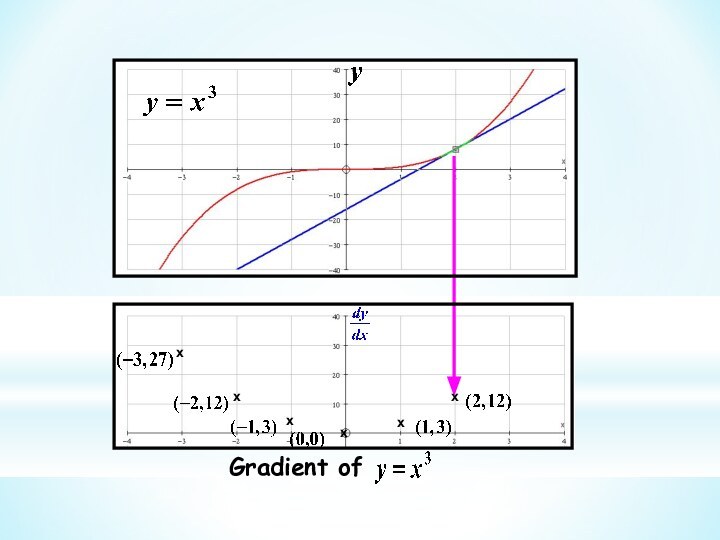
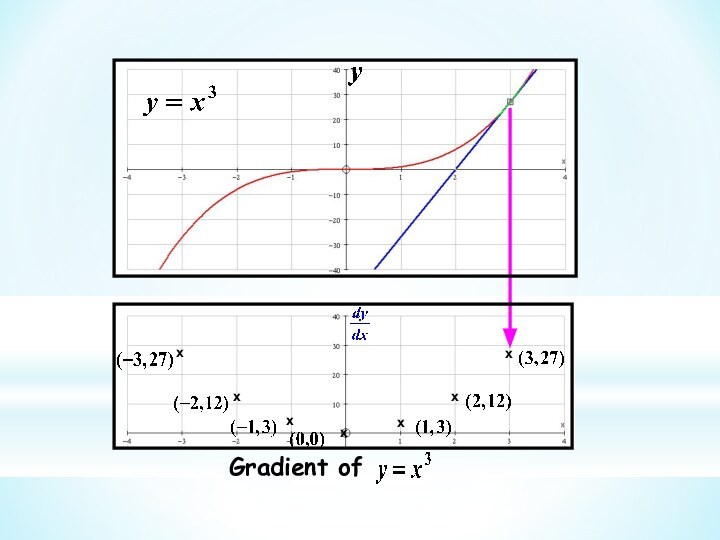
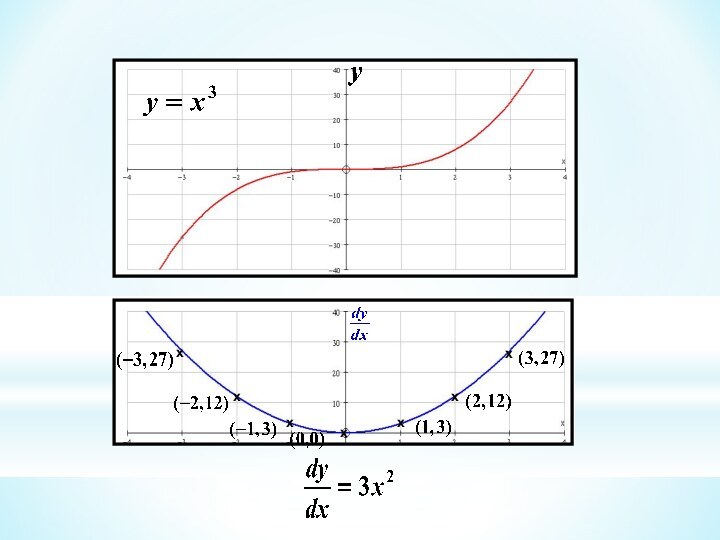
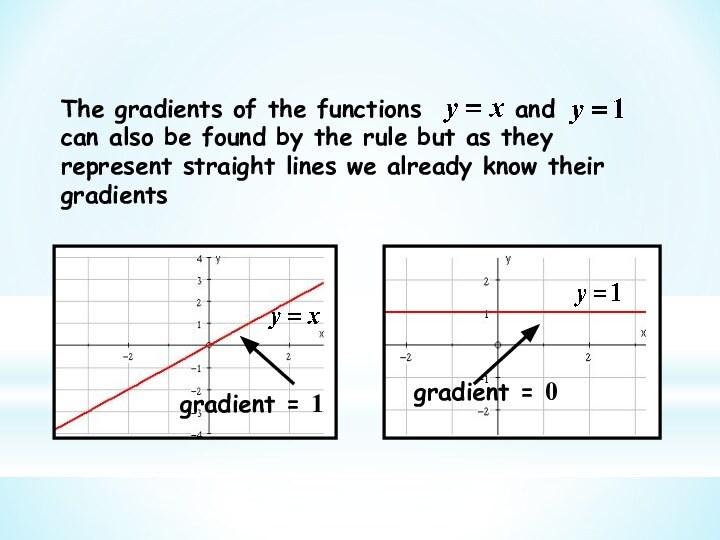




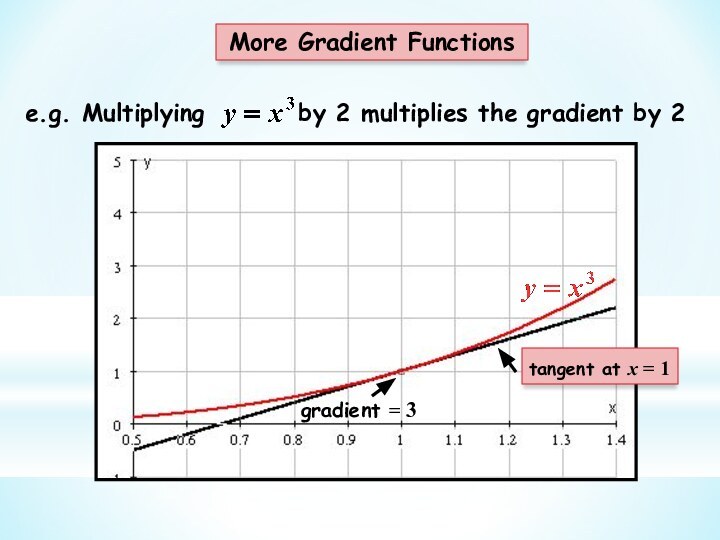






This branch of Mathematics is called Calculus
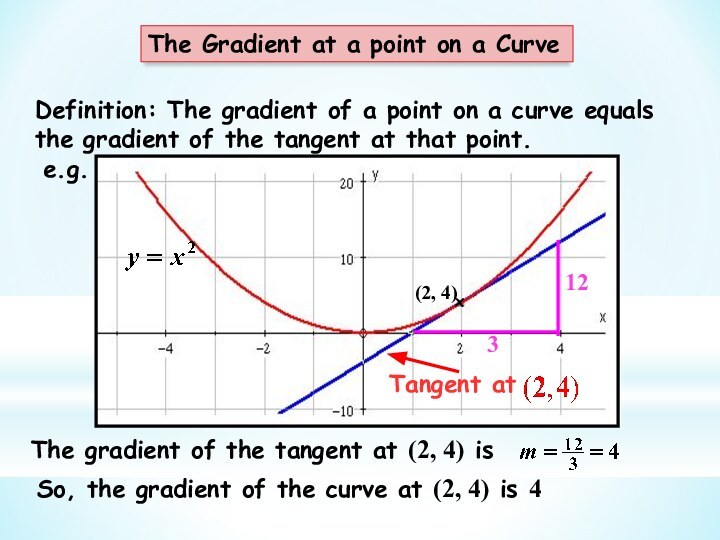
e.g.
3
12
So, the gradient of the curve at (2, 4) is 4
The process of finding the gradient function is called differentiating
The function that gives the gradient of a curve at any point is called the gradient function
The rule for differentiating terms of the form