ЦЕЛИ:
Образовательная –
закрепить навыки решения квадратных уравнений и
заданий, связанных с ними, различными способами.
развивать логическое мышление, способность мыс-
лить, решать учебные задачи и работать с дополни-
тельной литературой.
Развивающая -
Воспитательная -
прививать интерес к предмету, формировать комму-
никативные и волевые качества, воспитывать твор-
ческую личность.
Слайд 3
Основополагающий вопрос:
Как решать квадратные уравнения?
Вопросы учебной
темы:
Как решать неполные квадратные уравнения? Как определять количество
корней квадратного уравнения? Как решать приведенные квадратные уравнения по теореме Виета?
Учебные предметы: Алгебра
Участники проекта: 8 класс
Информационные ресурсы:
Интернет, печатные издания, мультимедийные приложения.
Слайд 4
РАЗ, ДВА, ТРИ, ЧЕТЫРЕ, ПЯТЬ
НАЧИНАЕМ МЫ СЧИТАТЬ…
БЕГАТЬ, ПРЫГАТЬ.МЫ
НЕ БУДЕМ
БУДЕМ ВЕСЬ УРОК РЕШАТЬ
НАСТРОИМСЯ НА УРОК
Слайд 5
Способы решения квадратных уравнений.
1. СПОСОБ: Разложение левой части
уравнения на множители.
Решим уравнение х2 + 10х - 24
= 0. Разложим левую часть на множители:
х2 + 10х - 24 = х2 + 12х - 2х - 24 = х(х + 12) - 2(х + 12) = (х + 12)(х - 2).
Следовательно, уравнение можно переписать так:
(х + 12)(х - 2) = 0
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = - 12. Это означает, что число 2 и - 12 являются корнями уравнения х2 + 10х - 24 = 0.
Слайд 6
2. СПОСОБ: Решение квадратных уравнений по формуле.
Умножим обе
части уравнения
ах2 + bх + с = 0, а
≠ 0
на 4а и последовательно имеем:
4а2х2 + 4аbх + 4ас = 0,
((2ах)2 + 2ах • b + b2) - b2 + 4ac = 0,
(2ax + b)2 = b2 - 4ac,
2ax + b = ± √ b2 - 4ac,
2ax = - b ± √ b2 - 4ac,
Слайд 7
О теореме Виета.
«Если В + D, умноженное на
А - А2, равно ВD, то А равно В
и равно D».
На языке современной алгебры вышеприведенная формулировка Виета означает: если имеет место
(а + b)х - х2 = ab,
т.е.
х2 - (а + b)х + аb = 0,
то
х1 = а, х2 = b.
Слайд 8
3. СПОСОБ: Решение уравнений с использованием теоремы Виета.
Как
известно, приведенное квадратное уравнение имеет вид
х2 + px +
c = 0. (1)
Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид
x1 x2 = q,
x1 + x2 = - p
а) x2 – 3x + 2 = 0; x1 = 2 и x2 = 1, так как q = 2 > 0 и p = - 3 < 0;
x2 + 8x + 7 = 0; x1 = - 7 и x2 = - 1, так как q = 7 > 0 и p= 8 > 0.
б) x2 + 4x – 5 = 0; x1 = - 5 и x2 = 1, так как q= - 5 < 0 и p = 4 > 0;
x2 – 8x – 9 = 0; x1 = 9 и x2 = - 1, так как q = - 9 < 0 и p = - 8 < 0.
Слайд 9
4. СПОСОБ: Свойства коэффициентов квадратного уравнения.
А. Пусть дано
квадратное уравнение ах2 + bх + с = 0,
где а ≠ 0.
1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х1 = 1,
х2 = с/а.
Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение
x2 + b/a • x + c/a = 0.
Согласно теореме Виета
x1 + x2 = - b/a,
x1x2 = 1• c/a.
По условию а – b + с = 0, откуда b = а + с. Таким образом,
x1 + x2 = - а + b/a= -1 – c/a,
x1x2 = - 1• ( - c/a),
т.е. х1 = -1 и х2 = c/a, что и требовалось доказать.
Слайд 10
Б. Если второй коэффициент b = 2k –
четное число, то формулу корней
В. Приведенное уравнение
х2 + рх
+ q= 0
совпадает с уравнением общего вида, в котором а = 1, b = р и с = q. Поэтому для приведенного квадратного уравнения формула корней
Слайд 11
5. СПОСОБ: Графическое решение квадратного уравнения.
Если в
уравнении
х2 + px + q = 0
перенести второй
и третий члены в правую часть, то получим
х2 = - px - q.
Построим графики зависимости у = х2 и у = - px - q.
Слайд 12
• Пример
Решим графически уравнение
х2 - 3х
- 4 = 0 (рис. 2).
Решение. Запишем уравнение в
виде
х2 = 3х + 4.
Построим параболу у = х2 и прямую
у = 3х + 4.
Прямую
у = 3х + 4 можно построить по двум точкам
М (0; 4) и N (3; 13).
Ответ: х1 = - 1; х2 = 4
Слайд 14
Группа 1
Решите уравнения
рациональным способом
а) х²+15х=0
б) 5х²-25=0
в) -9х+5х²=2
г)
2х²+4х=6
д)2х²-9=7х
Группа 2
Решите уравнения
рациональным способом
а) -5х²+4х=0
б) 7х²-49=0
в) 7х+2х²=-3
г) 5х²+2х=3
д)3х²+2=5х
Математика и
физика
Слайд 16
Ответы
Группа 1 ЭЙЛЕР
математик,
механик, физик и астроном. По происхождению швейцарец. В 1726
был приглашен в Петербургскую АН и переехал в 1727 в Россию. Автор св. 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближенным вычислениям, небесной механике, математической физике, оптике, кораблестроению, теории музыки
Группа 2 БИНОМ
НЬЮТОНА БИНОМ, формула, выражающая целую положительную степень суммы двух слагаемых
Частными случаями бинома Ньютона при n=2 и n=3 являются формулы квадрата и куба суммы двух слагаемых x и y.
Слайд 17
Сесть на краешек стула.
Поднять руки, потянуться, напрячь мышцы.
Вытянуть
руки перед грудью, потянуться.
Руки в стороны, потянуться, напрячь мышцы.
Обхватить
себя руками, выгнуть спину.
Принять рабочее положение.
ФИЗКУЛЬТУРНАЯ ПАУЗА
Слайд 18
Решения уравнений
х²+3х-5=0
2х²+3х+1=0
5х²-8х+3=0
Слайд 19
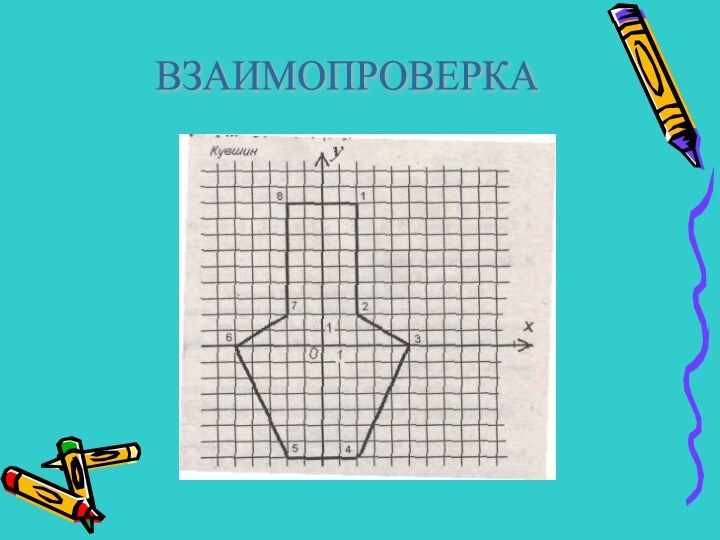
Задание «Кувшин»
«КОД») (x1,x2 или (x2,x1)- координаты точек координатной
плоскости.
Меньшее значение корня обозначить x1,большее обзначить x2
(x2 >
x1; x1
1) x2-11x+18=0; (x1,x2);
2) x2-4x+4=0; (x1,x2);
3) 2x2-10x=0; (x2,x1);
4) x2+5x-14=0; (x2,x1);
5) x2+9x+14=0; (x2,x1);
6) 3x2+15=0; (x1,x2);
7) 3x2-12=0; (x1,x2);
8) 2x2-14x-36=0; (x1,x2)
Слайд 21
Творческое задание (по желанию) изготовить дидактический материал по
теме: “Решения квадратных уравнений”.
Домашнее задание
Слайд 22
МЫ БУДЕМ УЧИТЬСЯ, РАБОТАТЬ С ОХОТОЙ
И НИЧЕГО
НЕ ПОПРОСИМ ВЗАМЕН
КАК ХОРОШО, ЧТО ЕСТЬ НА СВЕТЕ
ДВЕ ДРУЖНЫЕ
КОМАНДЫ:
УЧАЩИХСЯ И УЧИТЕЛЕЙ!