- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Классическое определение вероятности
Содержание
- 2. Теория вероятностей Развитие теории вероятностей с
- 3. Основатели теории вероятностей Основателями теории вероятностей
- 4. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТИ.
- 5. СОБЫТИЕ Под СОБЫТИЕМ понимается
- 6. Эксперимент (опыт) ЭКСПЕРИМЕНТ (или опыт) заключается
- 7. ПРИМЕРЫсдача экзамена, наблюдение за дорожно-транспортными происшествиями, выстрел из винтовки, бросание игрального кубика, химический эксперимент,и т.п.
- 8. СТАТИСТИЧЕСКИЙ Эксперимент называют СТАТИСТИЧЕСКИМ, если он
- 9. СЛУЧАЙНОЕ СОБЫТИЕ СЛУЧАЙНЫМ называют событие, которое
- 10. Рассмотрим несколько наиболее «излюбленных» в теории вероятностей примеров случайных экспериментов.
- 11. Опыт 1: Подбрасывание монеты. Испытание
- 12. Опыт 2: Подбрасывание кубика. Это
- 13. Опыт 3: Выбор перчаток. В
- 14. События А и В называют несовместными ,если
- 15. Типы событийДОСТОВЕРНОЕНЕВОЗМОЖНОЕСЛУЧАЙНОЕ
- 16. Типы событий Событие называется
- 17. Примеры событийдосто-верныеслу-чайныеневоз-можные1. ПОСЛЕ ЗИМЫ НАСТУПАЕТ ВЕСНА.2. ПОСЛЕ
- 18. Охарактеризуйте события, о которых идет речь в
- 19. Задание 2 В мешках лежит 10 шаров:
- 20. ИСХОД ИСХОДОМ (или элементарным исходом,
- 21. Число возможных исходов в каждом из рассмотренных
- 22. Однозначные исходы предполагают единственный результат того или
- 23. Неоднозначные исходы предполагают несколько различных результатов того
- 24. Запишите множество исходов для следующих испытаний.а) В
- 25. Задание 4 Найдите количество возможных исходов. а)
- 26. Задание 5 В каждом из следующих опытов
- 27. Благоприятный исход: Исход испытания называется благоприятным событию
- 28. ПОНЯТИЕ ВЕРОЯТНОСТИ
- 29. Известно, по крайней мере, шесть
- 30. КЛАССИЧЕСКОЕСТАТИСТИЧЕСКОЕГЕОМЕТРИЧЕСКОЕОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
- 31. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
- 32. ВЕРОЯТНОСТЬ– ЭТО ЧИСЛЕННАЯ МЕРА ОБЪЕКТИВНОЙ ВОЗМОЖНОСТИ ПОЯВЛЕНИЯ
- 33. Вероятностью Р наступления случайного события
- 34. Пьер-Симо́н Лапла́с Классическое определение вероятности было впервые дано в работах французского математика Лапласа.
- 35. Бросаем монетку2Выпал «орел»1Вытягиваем экзаменаци- онный билетВытянули билет
- 36. Пример 1 В школе 1300 человек, из
- 37. Вероятность: P(A) = 5/1300 = 1/250.Решение
- 38. Пример 2. При игре в нарды бросают
- 39. РешениеСоставим следующую таблицуВероятность: P(A)=6/36= =1/6.
- 40. Пример 3.Из карточек составили слово «статистика». Какую карточку с буквой вероятнее всего вытащить? Какие события равновероятные?статистика
- 41. Всего 10 букв.Буква «с» встречается 2 раза
- 42. Свойства вероятности
- 43. Вероятность достоверного события равна Вероятность невозможного события
- 44. P(u) = 1 (u – достоверное событие);P(v)
- 45. Задача 1. В коробке 4 синих, 3
- 46. а) Мы имеем всевозможных случаев 9. Благоприятствующих
- 47. Задача 2. В коробке лежат 10 одинаковых
- 48. Задача 3. Мальчики играли в “Орлянку”. Но
- 49. Считать "орел" - четное число, а "решка"
- 50. Задача 5. В настольной игре сломалась вертушка
- 51. Скачать презентацию
- 52. Похожие презентации













































Слайд 3
Основатели теории вероятностей
Основателями теории вероятностей были
французские математики Б. Паскаль и П. Ферма, и голландский ученый Х. Гюйгенс
Б. Паскаль
П.Ферма
Х. Гюйгенс
Слайд 5
СОБЫТИЕ
Под СОБЫТИЕМ понимается явление,
которое происходит в результате осуществления какого-либо определенного
эксперимента.ПРИМЕР. Бросаем шестигранный игральный кубик.
Определим события:
А {выпало четное число очков};
В {выпало число очков, кратное 3};
С {выпало более 4 очкков}.
✔
Слайд 6
Эксперимент (опыт)
ЭКСПЕРИМЕНТ (или опыт) заключается в
наблюдении за объектами или явлениями в строго определенных условиях
и измерении значений заранее определенных признаков этих объектов (явлений).✔
Слайд 7
ПРИМЕРЫ
сдача экзамена,
наблюдение за дорожно-транспортными происшествиями,
выстрел из
винтовки,
бросание игрального кубика,
химический эксперимент,
и т.п.
Слайд 8
СТАТИСТИЧЕСКИЙ
Эксперимент называют СТАТИСТИЧЕСКИМ, если он может
быть повторен в практически неизменных условиях неограниченное число раз.
✔
Слайд 9
СЛУЧАЙНОЕ СОБЫТИЕ
СЛУЧАЙНЫМ называют событие, которое может
произойти или не произойти в результате некоторого испытания (опыта).
Обозначают заглавными буквами А, В, С, Д,… (латинского алфавита).✔
Слайд 10 Рассмотрим несколько наиболее «излюбленных» в теории вероятностей примеров
случайных экспериментов.
Слайд 11
Опыт 1:
Подбрасывание монеты.
Испытание – подбрасывание монеты; события – монета упала «орлом»
или «решкой».✔
«решка» - лицевая сторона монеты (аверс)
«орел» - обратная сторона монеты (реверс)
Слайд 12
Опыт 2:
Подбрасывание кубика.
Это следующий по популярности после монеты случайный эксперимент.
Испытание – подбрасывание кубика; события – выпало 1, 2, 3, 4, 5 или 6 очков (и другие).✔
Слайд 13
Опыт 3:
Выбор перчаток. В коробке
лежат 3 пары одинаковых перчаток. Из нее, не глядя,
вынимаются две перчатки.«Завтра днем – ясная погода».
Здесь наступление дня – испытание, ясная погода – событие.
✔
✔
Опыт 4:
Слайд 14
События А и В называют несовместными ,если они
не могут произойти одновременно
События называют равновозможными , каждое из
них е не имеет преимуществ в появлении чаще других.
Слайд 16
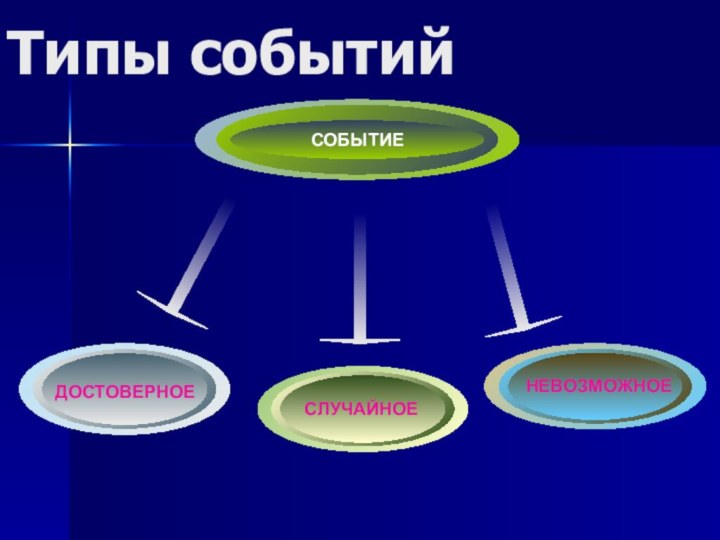
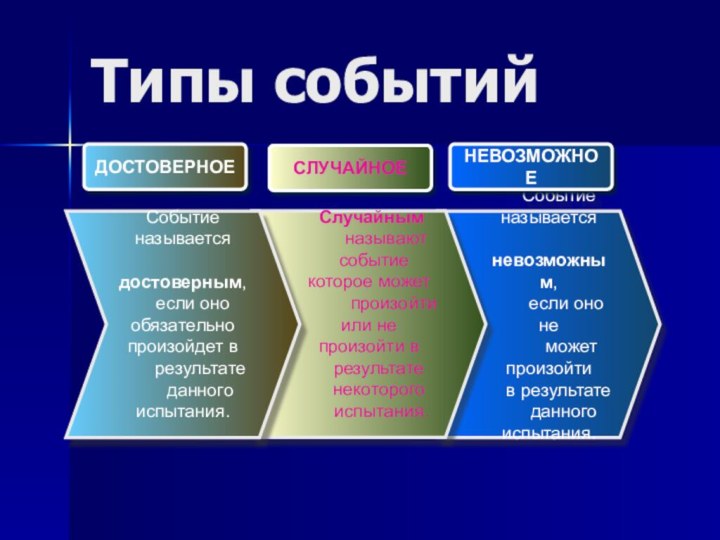
Типы событий
Событие называется
невозможным,
если оно не
может произойтив результате
данного испытания.
Случайным
называют
событие которое может
произойти или не произойти в
результате
некоторого
испытания.
Событие
называется
достоверным,
если оно обязательно произойдет в
результате
данного испытания.
ДОСТОВЕРНОЕ
СЛУЧАЙНОЕ
НЕВОЗМОЖНОЕ
Слайд 17
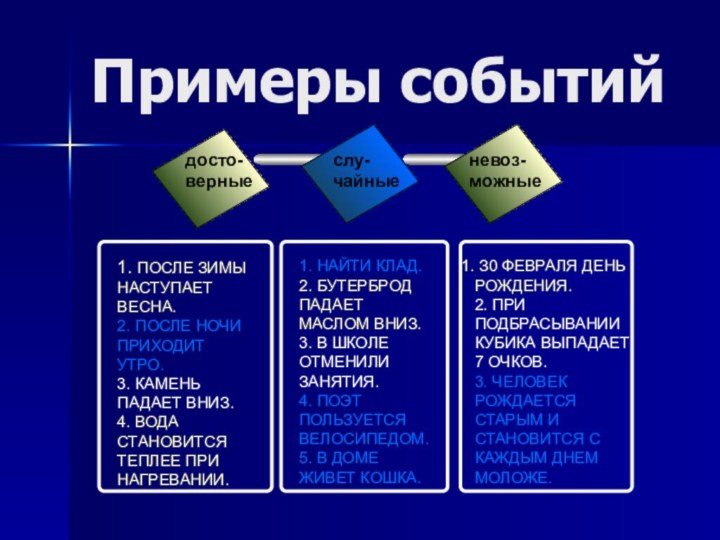
Примеры событий
досто-
верные
слу-
чайные
невоз-
можные
1. ПОСЛЕ ЗИМЫ НАСТУПАЕТ ВЕСНА.
2. ПОСЛЕ НОЧИ
ПРИХОДИТ УТРО.
3. КАМЕНЬ ПАДАЕТ ВНИЗ.
4. ВОДА СТАНОВИТСЯ ТЕПЛЕЕ ПРИ
НАГРЕВАНИИ. 1. НАЙТИ КЛАД.
2. БУТЕРБРОД ПАДАЕТ МАСЛОМ ВНИЗ.
3. В ШКОЛЕ ОТМЕНИЛИ ЗАНЯТИЯ.
4. ПОЭТ ПОЛЬЗУЕТСЯ ВЕЛОСИПЕДОМ.
5. В ДОМЕ ЖИВЕТ КОШКА.
З0 ФЕВРАЛЯ ДЕНЬ РОЖДЕНИЯ.
2. ПРИ ПОДБРАСЫВАНИИ КУБИКА ВЫПАДАЕТ 7 ОЧКОВ.
3. ЧЕЛОВЕК РОЖДАЕТСЯ СТАРЫМ И СТАНОВИТСЯ С КАЖДЫМ ДНЕМ МОЛОЖЕ.
Слайд 18 Охарактеризуйте события, о которых идет речь в приведенных
заданиях как достоверные, невозможные или случайные.
Петя задумал натуральное число.
Событие состоит в следующем:а) задумано четное число;
б) задумано нечетное число;
в) задумано число, не являющееся ни четным, ни нечетным;
г) задумано число, являющееся четным или нечетным.
Задание 1
Слайд 19
Задание 2
В мешках лежит 10 шаров: 3
синих, 3 белых и 4 красных.
Охарактеризуйте следующее событие:
а)
из мешка вынули 4 шара и они все синие;б) из мешка вынули 4 шара и они все красные;
в) из мешка вынули 4 шара, и все они оказались разного цвета;
г) из мешка вынули 4 шара, и среди них не оказалось шара черного цвета.
Слайд 20
ИСХОД
ИСХОДОМ (или элементарным исходом, элементарным
событием) называется один из взаимоисключающих друг друга вариантов, которым
может завершиться случайный эксперимент.✔
Слайд 21 Число возможных исходов в каждом из рассмотренных выше
опытах.
Опыт 1. – 2 исхода: «орел», «решка».
Опыт 2. – 6 исходов: 1, 2, 3, 4, 5, 6.Опыт 3. – 3 исхода: «обе перчатки на левую руку», «обе перчатки на правую руку», «перчатки на разные руки».
✔
✔
✔
Слайд 22 Однозначные исходы предполагают единственный результат того или иного
события: смена дня и ночи, смена времени года и
т.д.Слайд 23 Неоднозначные исходы предполагают несколько различных результатов того или
иного события:
при подбрасывании кубика выпадают разные грани; выигрыш
в Спортлото; результаты спортивных игр.
Слайд 24
Запишите множество исходов для следующих испытаний.
а) В урне
четыре шара с номерами два, три, пять, восемь. Из
урны наугад извлекают один шар.б) В копилке лежат три монеты достоинством в 1 рубль, 2 рубля и 5 рублей. Из копилки достают одну монету.
в) В доме девять этажей. Лифт находится на первом этаже. Кто-то из жильцов дома вызывает лифт на свой этаж. Лифтовый диспетчер наблюдает, на каком этаже лифт остановится.
Задание 3
Слайд 25
Задание 4
Найдите количество возможных исходов.
а) За
городом N железнодорожные станции расположены в следующем порядке: Луговая,
Сосновая, Озёрная, Дачная, Пустырь. Событие А – пассажир купил билет не далее станции Озёрная.б) Один ученик записал целое число от 1 до 5, а другой ученик пытается отгадать это число. Событие В – записано чётное число.
в) Вини Пух думает, к кому бы пойти в гости: к Кролику, Пяточку, ослику Иа-Иа или Сове? Событие А – Вини Пух пойдёт к Пяточку; событие В – Вини Пух не пойдёт к Кролику.
Слайд 26
Задание 5
В каждом из следующих опытов найдите
количество возможных исходов:
а) подбрасывание двух монет;
б) подбрасывание двух кнопок;
в)
подбрасывание двух кубиков;г) подбрасывание монеты и кубика;
д) подбрасывание монеты, кнопки и кубика.
Слайд 27
Благоприятный исход:
Исход испытания называется благоприятным событию А ,если
его наступление в результате опыта приводит к наступлению события
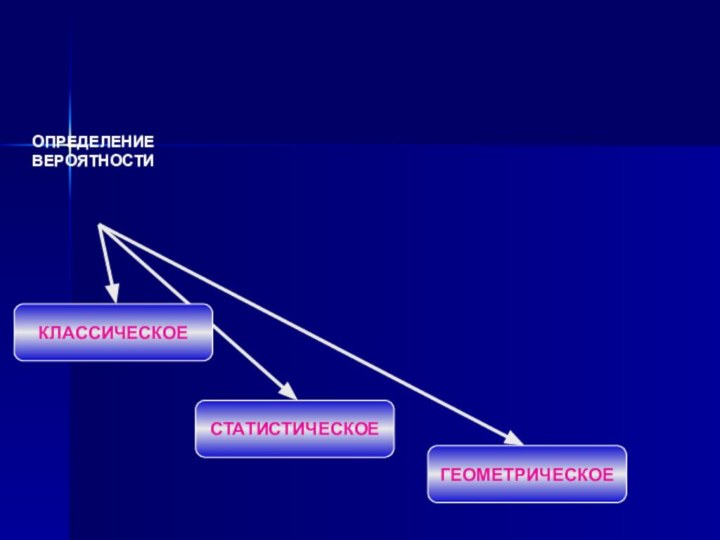
АСлайд 29 Известно, по крайней мере, шесть основных
схем определения и понимания вероятности. Не все они в
равной мере используются на практике и в теории, но, тем не менее, все они имеют за собой разработанную логическую базу и имеют право на существование.Понятие вероятности
Слайд 32
ВЕРОЯТНОСТЬ
– ЭТО ЧИСЛЕННАЯ МЕРА ОБЪЕКТИВНОЙ ВОЗМОЖНОСТИ ПОЯВЛЕНИЯ СЛУЧАЙНОГО
СОБЫТИЯ.
ТЕОРИЯ ВЕРОЯТНОСТЕЙ ДАЕТ СПОСОБ НАХОЖДЕНИЯ ЧИСЛЕННОГО ЗНАЧЕНИЯ
ВЕРОЯТНОСТИ СОБЫТИЯ:А – некоторое событие,
m – количество исходов, при которых событие А появляется,
n – конечное число равновозможных исходов.
P – обозначение происходит от первой буквы французского слова probabilite – вероятность.
Слайд 33 Вероятностью Р наступления случайного события А
называется отношение , где n – число всех
возможных исходов эксперимента, а m – число всех благоприятных исходов:КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ.
Слайд 34
Пьер-Симо́н Лапла́с
Классическое определение вероятности было впервые дано
в работах французского математика Лапласа.
Слайд 35
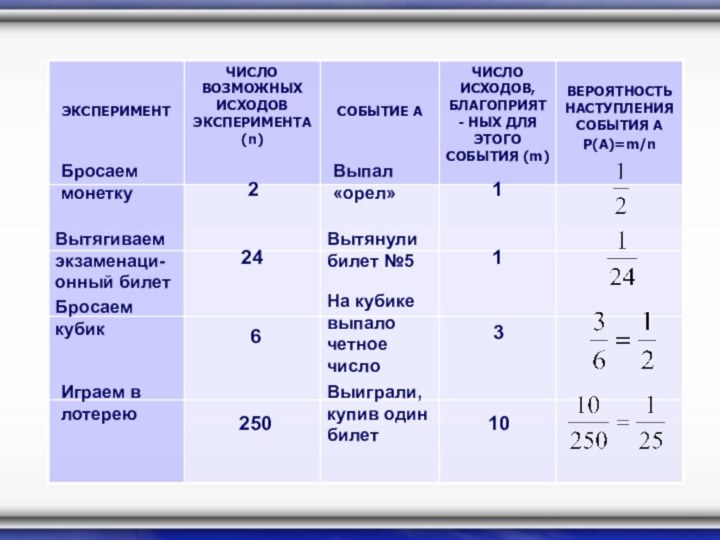
Бросаем монетку
2
Выпал «орел»
1
Вытягиваем экзаменаци- онный билет
Вытянули билет №5
24
1
Бросаем
кубик
На кубике выпало четное число
6
3
Играем в лотерею
Выиграли, купив один
билет
250
10
Слайд 36
Пример 1
В школе 1300 человек, из
них
5 человек хулиганы.Какова вероятность того, что один из них попадётся директору на глаза?
Слайд 38
Пример 2.
При игре в нарды бросают 2
игральных кубика. Какова вероятность того, что на обоих кубиках
выпадут одинаковые числа?
Слайд 40
Пример 3.
Из карточек составили слово «статистика». Какую карточку
с буквой вероятнее всего вытащить? Какие события равновероятные?
с
т
а
т
и
с
т
и
к
а
Слайд 41
Всего 10 букв.
Буква «с» встречается 2 раза –
P(с) = 2/10 = 1/5;
буква «т» встречается 3 раза
–P(т) = 3/10;
буква «а» встречается 2 раза –
P(а) = 2/10 = 1/5;
буква «и» встречается 2 раза –
P(и) = 2/10 = 1/5;
буква «к» встречается 1 раз –
P(к) = 1/10.
Решение
Слайд 43
Вероятность достоверного события равна
Вероятность невозможного события равна
Вероятность события А не меньше , но не
больше ?
1
?
?
?
0
1
0
Слайд 45
Задача 1.
В коробке 4 синих, 3 белых
и 2 желтых фишки. Они тщательно перемешиваются, и наудачу
извлекается одна из них. Найдите вероятность того, что она окажется: а) белой; б) желтой; в) не желтой.Задача 1.
В коробке 4 синих, 3 белых и 2 желтых фишки. Они тщательно перемешиваются, и наудачу извлекается одна из них. Найдите вероятность того, что она окажется: а) белой; б) желтой; в) не желтой.
Слайд 46 а) Мы имеем всевозможных случаев 9. Благоприятствующих событий
3. Вероятность равна:
P=3:9=1/3=0,33(3)
б) Мы имеем всевозможных случаев 9. Благоприятствующих
событий 2. Вероятность равна P=2:9=0,2(2)в) Мы имеем всевозможных случаев 9. Благоприятствующих событий 7 (4+3). Вероятность равна P=7:9=0,7(7)
а) Мы имеем всевозможных случаев 9. Благоприятствующих событий 3. Вероятность равна:
P=3:9=1/3=0,33(3)
б) Мы имеем всевозможных случаев 9. Благоприятствующих событий 2. Вероятность равна P=2:9=0,2(2)
в) Мы имеем всевозможных случаев 9. Благоприятствующих событий 7 (4+3). Вероятность равна P=7:9=0,7(7)
Решение
Слайд 47
Задача 2.
В коробке лежат 10 одинаковых шаров,
на каждом из которых написан его номер от 1
до 10. Найдите вероятность следующих событий: а) извлекли шар № 7; б) номер извлеченного шара – четное число; в) номер извлеченного шара кратен 3.Задача 2.
В коробке лежат 10 одинаковых шаров, на каждом из которых написан его номер от 1 до 10. Найдите вероятность следующих событий: а) извлекли шар № 7; б) номер извлеченного шара – четное число; в) номер извлеченного шара кратен 3.
Слайд 48
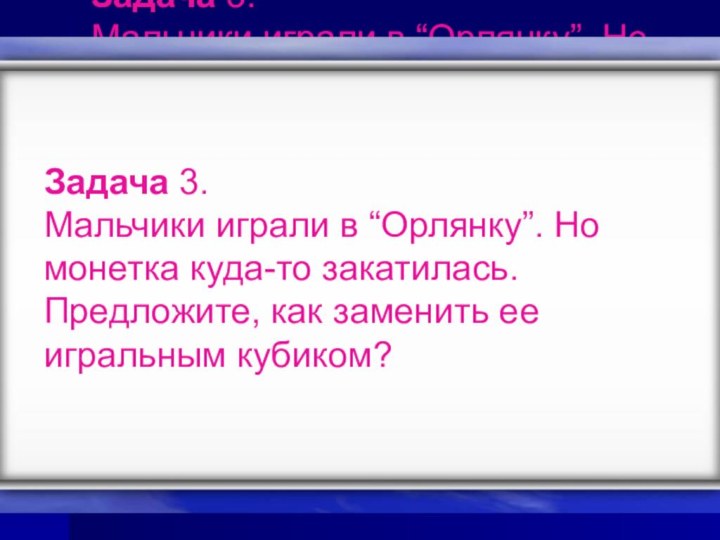
Задача 3.
Мальчики играли в “Орлянку”. Но монетка
куда-то закатилась. Предложите, как заменить ее игральным кубиком?
Задача 3.
Мальчики играли в “Орлянку”. Но монетка куда-то закатилась. Предложите, как заменить ее игральным кубиком?
Слайд 49 Считать "орел" - четное число, а "решка" -
не четное число.
Считать "орел" - четное число, а "решка"
- не четное число. Решение
Слайд 50
Задача 5.
В настольной игре сломалась вертушка с
тремя разными секторами: красным, белым и синим, но есть
кубик. Как заменить вертушку?Задача 5.
В настольной игре сломалась вертушка с тремя разными секторами: красным, белым и синим, но есть кубик. Как заменить вертушку?





























