Презентация на тему Функции в алгебре

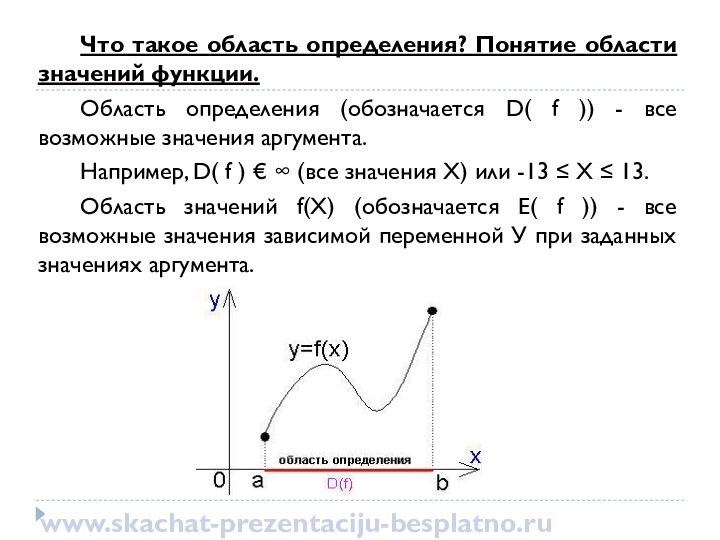
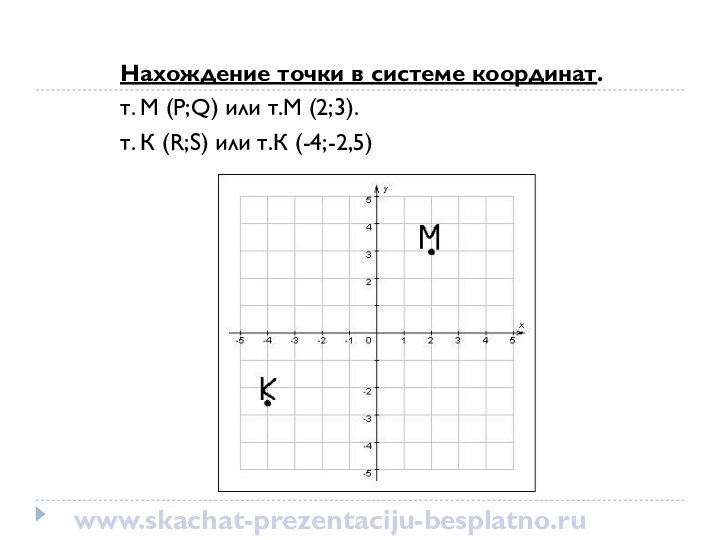
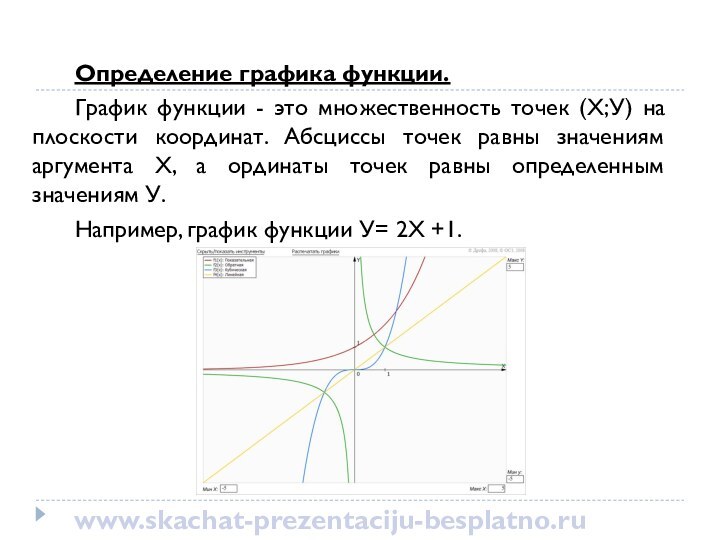
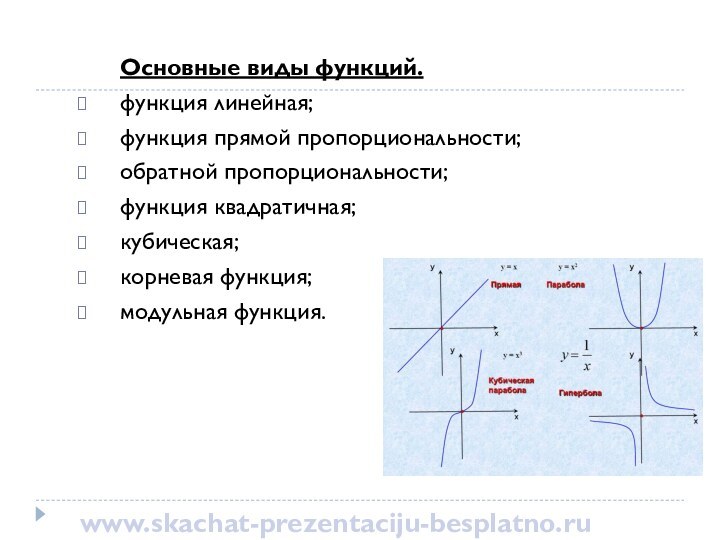
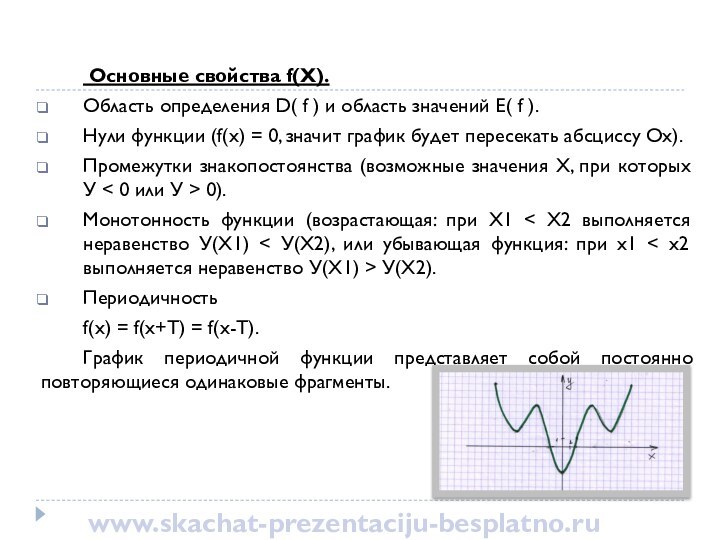
это математическая зависимость значений переменной У от заданных значений

переменной Х. При этом каждому определенному значению Х соответствует единственно возможное значение У. Переменная Х называется аргументом (или независимой переменной). Переменная У называется значением функции и является зависимой (от Х) переменной.

www.skachat-prezentaciju-besplatno.ru

У=f(x)

определения (обозначается D( f )) - все возможные значения

аргумента.
Например, D( f ) € ∞ (все значения Х) или -13 ≤ Х ≤ 13.
Область значений f(X) (обозначается Е( f )) - все возможные значения зависимой переменной У при заданных значениях аргумента.

www.skachat-prezentaciju-besplatno.ru

f(х). Например, У=2Х-4 или тождественное вырождение f(x)=2Х - 4.
f(-3)

= -10 - значение функции при конкретно заданном значении аргумента.
таблицы.
Например, для У=2Х-4:


Значение Х берется произвольное, «из головы», значение У высчитывается путем подстановки каждого значения Х в заданную формулу. Например, У1 = 2*(-3) - 4 = -10.
словесного описания;
графического отображения зависимости значения функции от аргумента.

www.skachat-prezentaciju-besplatno.ru

необходимо начертить декартову систему координат. Это две пересекающиеся под

прямым углом прямые (оси). Точка пересечения обозначается О. Вертикальная ось - ордината (У), горизонтальная ось - абсцисса (Х).

www.skachat-prezentaciju-besplatno.ru

т.М (2;3).
т. К (R;S) или т.К (-4;-2,5)

www.skachat-prezentaciju-besplatno.ru

(Х;У) на плоскости координат. Абсциссы точек равны значениям аргумента

Х, а ординаты точек равны определенным значениям У.
Например, график функции У= 2Х +1.

www.skachat-prezentaciju-besplatno.ru

функция;
модульная функция.

www.skachat-prezentaciju-besplatno.ru

и область значений Е( f ).
Нули функции (f(х) =

0, значит график будет пересекать абсциссу Ох). 
Промежутки знакопостоянства (возможные значения Х, при которых У < 0 или У > 0).
Монотонность функции (возрастающая: при Х1 < Х2 выполняется неравенство У(Х1) < У(Х2), или убывающая функция: при x1 < x2 выполняется неравенство У(Х1) > У(Х2).
Периодичность
f(x) = f(x+Т) = f(x-Т).
График периодичной функции представляет собой постоянно повторяющиеся одинаковые фрагменты.

www.skachat-prezentaciju-besplatno.ru

относительно точки пересечения осей системы координат.
При построении график четной

функции обязательно симметричен относительно вертикальной оси Оу.
f(-x) = f(x)
Нечетная функция.
D( f ) - симметрична относительно точки пересечения осей координат.
График нечетной функции всегда симметричен относительно точки пересечения осей системы координат.
f(-x) = –f(x)

www.skachat-prezentaciju-besplatno.ru