- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Практическое занятие элективного курса Функция: просто, сложно, интересно по теме Монотонность функции (9 класс)
Содержание
- 2. Методическая цель: организация деятельности, направленной на формирование
- 4. Содержание Теоретическая шпаргалкаЗадания для самостоятельного решения с
- 5. Теоретическая шпаргалка Определение возрастающей функцииОпределение убывающей функцииОпределение
- 6. Определение возрастающей функции Шпаргалка
- 7. Определение убывающей функции Шпаргалка
- 8. Определение монотонной функции Шпаргалка
- 9. Свойства монотонности функции
- 10. Свойство 2. Если функция y=f(x) монотонная на
- 11. Шпаргалка
- 12. Определение взаимно обратных функций Шпаргалка
- 13. Свойство взаимно обратных функций Шпаргалка
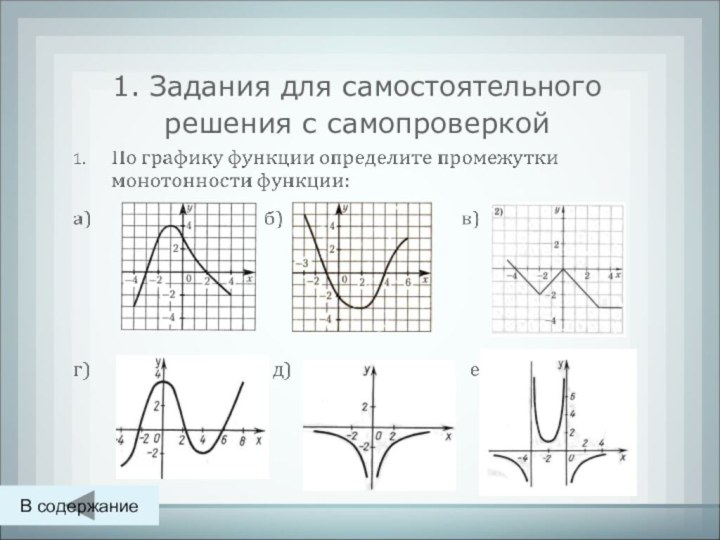
- 14. 1. Задания для самостоятельного решения с самопроверкой В содержание
- 15. 1. а) Самопроверка Задания
- 16. 1. б) Самопроверка Задания
- 17. 1. в) Самопроверка Задания
- 18. 1. г) Самопроверка Задания
- 19. 1. д) Самопроверка Задания
- 20. 1. е) Самопроверка Задания
- 21. 2. Задания для самостоятельного решения с самопроверкой В содержаниеПроверка
- 22. 2. Задания для самостоятельного решения с самопроверкой В содержаниеПроверка
- 23. 2. Задания для самостоятельного решения с самопроверкой В содержаниеПроверка
- 24. 2. а) б) Самопроверка Задание
- 25. 2. в) г) Самопроверка Заданиев) Б и Гг) Б и В
- 26. 2. д) Самопроверка Задание
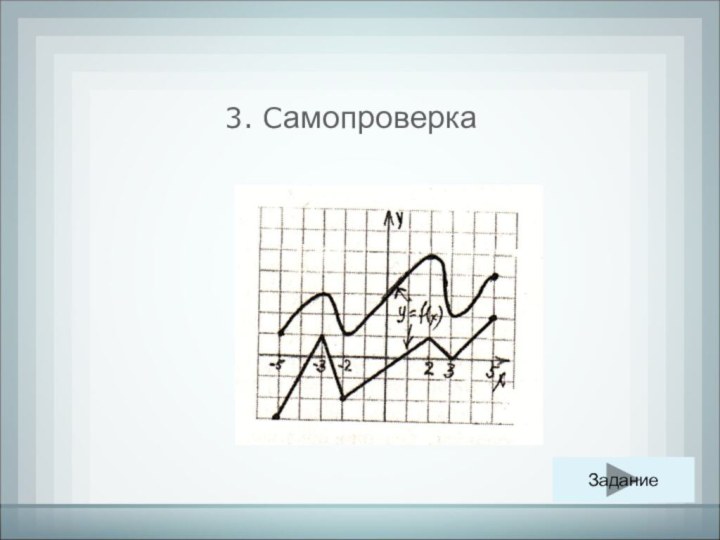
- 27. 3. Задание для самостоятельного решения с самопроверкой В содержаниеПроверка
- 28. 3. Самопроверка Задание
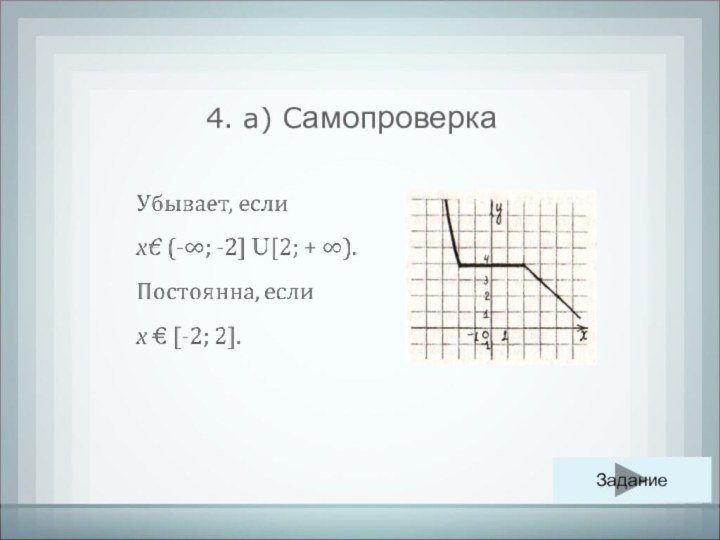
- 29. 4. Задания для самостоятельного решения с самопроверкой В содержаниеПроверка
- 30. 4. Задания для самостоятельного решения с самопроверкой В содержаниеПроверка
- 31. 4. а) Самопроверка Задание
- 32. 4. б) Самопроверка Задание
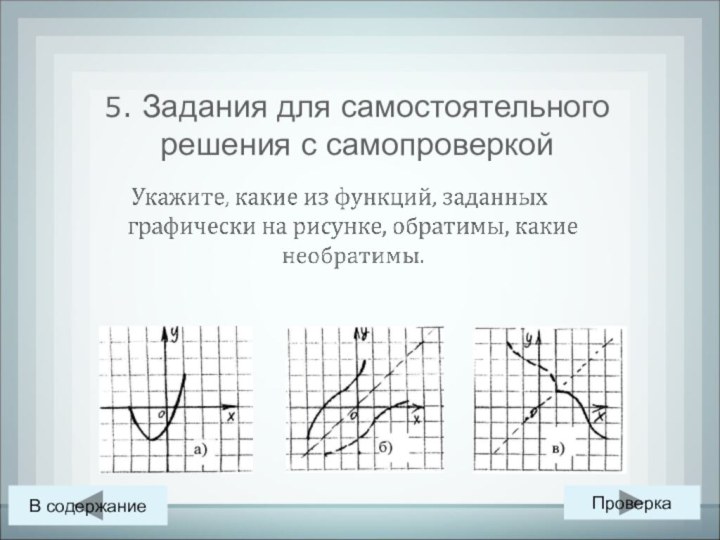
- 33. 5. Задания для самостоятельного решения с самопроверкой В содержаниеПроверка
- 34. 5. Самопроверка Задание
- 35. Скачать презентацию
- 36. Похожие презентации
Методическая цель: организация деятельности, направленной на формирование знаний и умений обучающихся на уровне, определённом стандартом образования.Образовательная цель: осознание понятий «возрастание», «убывание» функций: нахождение промежутков монотонности по графикам и формулам.































Слайд 2 Методическая цель: организация деятельности, направленной на формирование знаний
и умений обучающихся на уровне, определённом стандартом образования.
осознание понятий «возрастание», «убывание» функций: нахождение промежутков монотонности по графикам и формулам.
Слайд 4
Содержание
Теоретическая шпаргалка
Задания для самостоятельного решения с самопроверкой
1
1 , 2(а,б)1 , 2(а,б), 2(в,г)1 , 2(а,б), 2(в,г),
2(д)1 , 2(а,б), 2(в,г), 2(д), 31 , 2(а,б), 2(в,г), 2(д), 3, 4(а)1 , 2(а,б), 2(в,г), 2(д), 3, 4(а), 4(б)1 , 2(а,б), 2(в,г), 2(д), 3, 4(а), 4(б), 5Рефлексия
Слайд 5
Теоретическая шпаргалка
Определение возрастающей функции
Определение убывающей функции
Определение монотонной
функции
Свойства монотонности функций
Определение взаимно обратных функций
Свойство взаимно обратных
функцийВ содержание
Слайд 10 Свойство 2. Если функция y=f(x) монотонная на множестве
Х и сохраняет на этом множестве знак (то есть
все её значения являются положительными или отрицательными), то функция g(x)= 1∕ f(x) имеет на множестве Х противоположный характер монотонности.Доказательство:
Пусть функция y=f(x) возрастающая на множестве Х. Возьмём на множестве Х значения x1 и x2 , такие, что x2 >x1 и рассмотрим разность f(x2) - f(x1)>0; рассмотрим
g(x2) - g(x1) = 1 - 1 = f(x1) - f(x2) <0
f(x2) f(x1) f(x2) ∙f(x1)
Значит g(x2)





























