- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку алгебры 10 класс
Содержание
- 2. Нет ни одной области в математике, которая
- 3. Применение производнойПроизводная в физикеГеометрический смысл производной Уравнение касательной к графику функции
- 4. Найди пару: f (xo)-------f / (xo)X3
- 5. Производная функции, описывающей движение тела, равна скорости
- 6. Зависимость пути от времени движения задана формулой s(t)=t 2+2t. Найдите скорость, если t=1,8c.
- 7. s(t)= t 2+2tS / (t)=V(t)=2t+2V(1,8)=3,6+2=5,6(м/с)
- 8. f / (хо)= tg(A)=k Геометрический смысл производной
- 9. задание1. На рисунке изображён график
- 10. задание2 На рисунке изображен
- 11. Записываем уравнение касательной: у= f
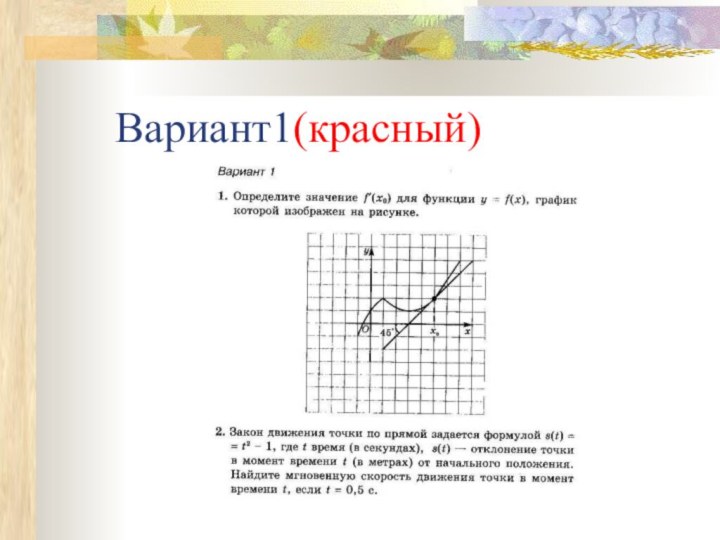
- 13. Вариант1(красный)
- 15. Вариант2(синий)
- 17. Вариант3(зелёный)
- 20. Находим f / (x)Определяем критические точки функции
- 21. Таблица производных Производные элементарных функций: Производные сложных функций: Обращение к таблице
- 22. Производная Обучающий блок
- 24. Производная функции, описывающей движение тела, равна скорости
- 25. Находим область определения функции У=f(x)Вычисляем производную функции
- 26. Скачать презентацию
- 27. Похожие презентации
Нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира … Н.И. Лобачевский

























Слайд 3
Применение производной
Производная в физике
Геометрический смысл производной
Уравнение касательной
к графику функции
Слайд 4
Найди пару: f (xo)-------f / (xo)
X3
sin3x
10x+3 1/x3
3sin x (5x+7)2
1/x x/10
3cos3x; (7x6 +3); 10; 3x2; -1/x2 ;
-3/x4; 10(5x+7); 0,1; 3 cos x; (x7 +3х)
Слайд 5
Производная функции, описывающей движение тела, равна скорости
S / (х)=V(х)
Производная функции, описывающей скорость тела, равна ускорению
V / (х)=А(х)Производная в физике
Слайд 6 Зависимость пути от времени движения задана формулой s(t)=t
2+2t. Найдите скорость, если t=1,8c.
Слайд 9 задание1. На рисунке изображён график функции и касательная к
нему в точке с абсциссой Найдите значение производной
функции в точке .
Слайд 10 задание2 На рисунке изображен график производной функции , определенной
на интервале . Найдите количество точек, в которых касательная
к графику функции параллельна прямой или совпадает с ней.
Слайд 11
Записываем уравнение касательной:
у= f (xo)+f
/ (xo)(x-xо)
Находим f(хо )
Находим производную у / =f / (x)
Вычисляем значение f / (х) в точке хо:
f / (хо)
Подставляем значение f(хо ), f / (хо), хо в уравнение касательной.
Уравнение касательной к графику функции
Слайд 20
Находим f / (x)
Определяем критические точки функции f(x),
т.е. точки, в которых f / (x)=0 или f
/ (x) не существует. Располагаем их в порядке возрастания.Определяем знак f / (х) на каждом из промежутков (а;в) в критических точках
Находим максимум и минимум
Находим экстремальные значения функции в точках максимум и минимум
Если не указан интервал, на котором исследуется функция у=f(х) на экстремум, то вначале следует найти область ее определения, а потом см.начало
Алгоритм нахождения экстремумов функции
Слайд 21
Таблица производных
Производные элементарных функций:
Производные сложных функций:
Обращение к таблице
Слайд 24
Производная функции, описывающей движение тела, равна скорости
S / (х)=V(х)
Производная функции, описывающей скорость тела, равна ускорению
V / (х)=А(х)Производная в физике
Слайд 25
Находим область определения функции У=f(x)
Вычисляем производную функции f
/(x)
Решаем неравенства:
а) f / (x)>0,
находим промежутки возрастания функции у=f(x); б) f / (х)<0, находим промежутки убывания функции у=f(х).
Решение неравенства выполняется аналитически, либо методом интервалов.
Алгоритм отыскания промежутков возрастания и убывания функции





























