Презентация на тему по математике на тему ЕГЭ Задача № 19-теория чисел часть 3 (11 класс)

является) самой сложной на ЕГЭ по математике?
Она нестандартна.

Она требует математической культуры — умения грамотно строить рассуждения.
Учиться культурно рассуждать можно и обязательно нужно.
Задача №19 предоставляет для этого отличную возможность.

Надо мыслить
нестандартно

2,  3, …,  n – 1,  n, п +

1, …
Функцию y = f(x), x  N называют функцией натурального аргумента или числовой последовательностью и обозначают y = f(n) или  y1,  y2, …, yn, … или {уn}.

Величина уn называется общим членом последовательности.

Обычно числовая последовательность задаётся некоторой формулой уn = f(n), позволяющей найти любой член последовательности по его номеру n;
эта формула называется формулой общего члена.

ряд натуральных чисел;
2,  4,  6,  8,  10, … –

ряд чётных чисел;
1, 4, 9, 16, 25, … – ряд квадратов натуральных чисел;
5, 10, 15, 20, … – ряд натуральных чисел, кратных 5;
1, 1/2, 1/3, 1/4, 1/5, ... – ряд вида 1/n, где nN;
и т.д.

рекуррентной формулы.
Примеры:
Последовательность простых чисел:
2; 3; 5; 7;

11; 13; 17; 19; 23; 29; …
Арифметическая прогрессия:
an = a1 + (n – 1)d
Геометрическая прогрессия:
bn + 1 = bn ∙ q

3; 5; 7; … ; б) 5; 8; 11;

14; … ; в) 1; 4; 9; 16; … ;
г) 1; - 2; 3; - 4; …

Простейшие примеры

которой, начиная
со второго, равен предыдущему, увеличенному на одно

и то же число, которое называется разностью
арифметической прогрессии.

Формула n-ого члена – позволяет вычислить член арифметической прогрессии с любым заданным номером
аn= а1 + d(n – 1),

где а1 – первый член арифметической прогрессии и d – разность арифметической прогрессии

которой,
начиная со второго, равен предыдущему, умноженному
на одно и

то же число, которое называется
знаменателем геометрической прогрессии.

есть среднее арифметическое между предыдущим и последующим членами прогрессии
Каждый

член последовательности начиная со второго есть среднее геометрическое между предыдущим и последующим членами последовательности
(bn >0)

арифметическая

геометрическая

почтовые марки на общую сумму 2 р. 80 к.

Определить стоимость марок, приобретенных отправителем, если эти стоимости составляют арифметическую прогрессию, а самая дорогая марка в 2,5 раза дороже самой дешевой.

Простейшие примеры

= 8, а52 = 12. Найдите разность арифметической прогрессии.
1)

0,5

2) 14

3) 11

4) 2

3. Члены некоторой бесконечной арифметической прогрессии изображены (рис.1) точками на координатной плоскости. Какое из данных чисел является членом этой прогрессии?

4. Найдите сумму семи первых членов геометрической прогрессии 4; 8; …

1) 556

2) 508

3) 658

4) 524

2) 18

3) 3

4) 9

1) -3

1) -7

3) 12

4) 18

2) 6

Простейшие примеры

b3 = 24. Найдите b5. ( для q >

0 )

Ответ: 72

7. Сумма второго и пятого членов арифметической прогрессии равна 11. Третий её член на 6 больше первого. Найдите второй и четвёртый члены этой прогрессии.

Ответ: 1 и 7

Простейшие примеры

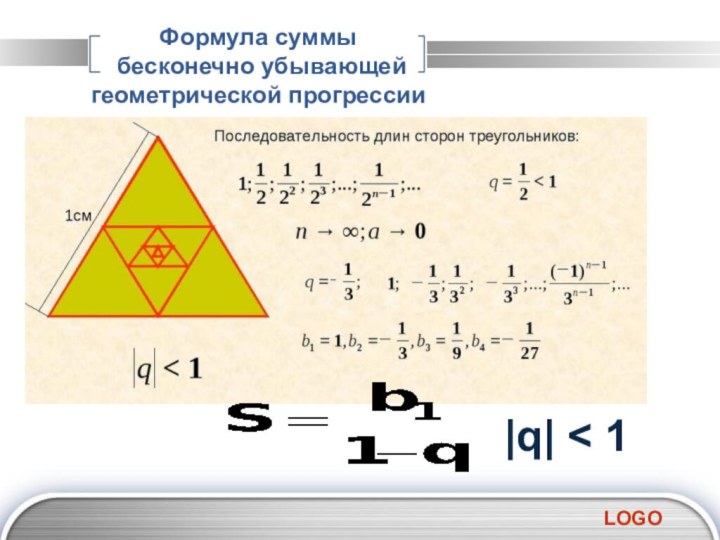
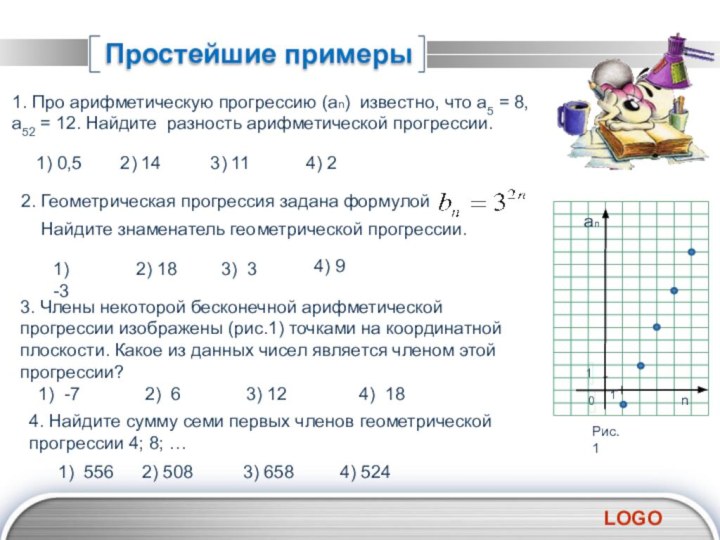
∙ 9 = 100;
S₁₀ = ½(100+280) ∙ 10 =1900.
Ответ:1900

человек вмещает амфитеатр.

8.Решение:
S₁₆=½ (2∙а₁ + 3∙15) ∙16;
472 =16 а₁ + 360;
а₁ = (472- 360):16=7.
а₁₆ =7+ 3 ∙ (16-1)=52.
Ответ: 52 коралла украл Карл в последний день.
9.Решение: 240=½(2 а₁ +2 ∙14) ∙ 15;
240:15= а₁ + 14; а₁ = 2;
а₁₁ = 2+2 ∙ 10 = 22.
Ответ:22 задачи надо решить 12 мая.

Простейшие примеры

10.В амфитеатре расположены 10 рядов, причем в каждом следующем ряду на 20 мест больше чем в предыдущем, а в последнем ряду 280 мест. Сколько человек вмещает амфитеатр?

8. За 16 дней Карл украл у Клары 472 коралла. Каждый день он крал на 3 коралла больше, чем в предыдущий день. Сколько кораллов украл Карл в последний день.
9.В сборнике по подготовке к экзамену-240 задач. Ученик планирует начать их решение 2 мая, а закончить 16 мая, решая каждый день на две задачи больше, чем в предыдущий день. Сколько задач ученик запланировал решить 12 мая?

член этой последовательности, начиная со второго, либо в 13

раз больше, либо в 13 раз меньше предыдущего. Сумма всех членов последовательности равна 6075.
Может ли последовательность состоять из трёх членов?
Может ли последовательность состоять из двух членов?
Какое наибольшее количество членов может быть в этой последовательности?

А теперь задачи уровня ЕГЭ…

п ≥ 3.
а) Может ли сумма всех данных

чисел быть равной 18?
б) Каково наибольшее значение п, если сумма всех данных чисел меньше 800?
в) Найти все возможные п, если сумма значений всех данных чисел равна 111.

А теперь задачи уровня ЕГЭ…

ли такие прогрессии, для которых

б) Существуют ли такие прогрессии, для которых
в) Какое наибольшее значение может принимать произведение а3b3, если

А теперь задачи уровня ЕГЭ…