Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему История комплексных чисел

Содержание

2. 1. Развитие понятия о числе Древнегреческие математики
3. 1. Развитие понятия о числе Введение отрицательных
4. 2. На пути к комплексным числамВ XVI
5. В формуле для решения кубических уравнений вида:
6. кубические и квадратные корни:
7. Эта формула безотказно действует в случае, когда
8. x=1
9. Кроме х=1, есть еще два корня
10. Итальянский алгебраист Дж. Кардано в 1545 г.
11. не имеющая решений во множестве действительных чисел, имеет решения вида
12. нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать что
13. 3. Утверждение комплексных чисел в математике Кардано
14. Название “мнимые числа” ввел в 1637 году
15. Слово комплекс (от латинского complexus) означает
16. Л. Эйлер вывел в 1748 году замечательную формулу
17. которая связывала воедино показательную функцию с
18. В конце XVIII века французский математик Ж.
19. После создания теории комплексных чисел возник
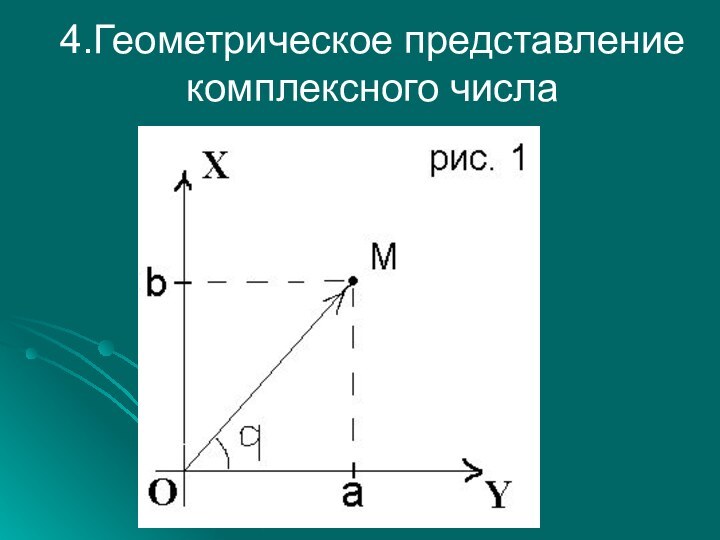
21. 4.Геометрическое представление комплексного числа
22. Такая плоскость называется комплексной. Вещественные числа на
23. 5. Тригонометрическая форма комплексного числа. Абсцисса а
24. Комплексные числа, несмотря на их “лживость” и
25. Поэтому всякое комплексное число можно представить в
26. Скачать презентацию
27. Похожие презентации

1. Развитие понятия о числе Древнегреческие математики считали “настоящими” только натуральные числа. Наряду с натуральными числами применяли дроби - числа, составленные из целого числа долей единицы.

Главная
Алгебра
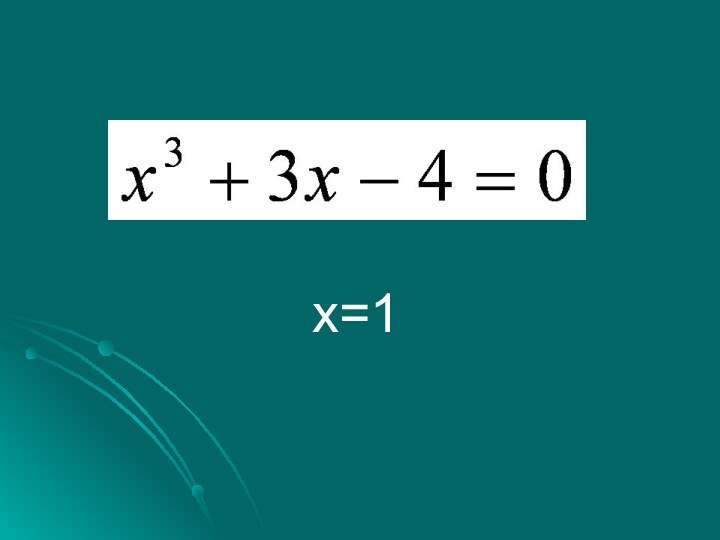
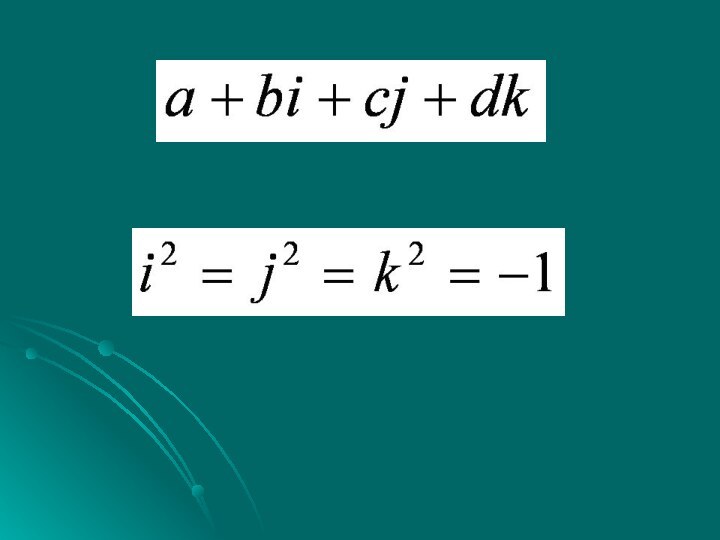
История комплексных чисел

Комплексные числаИстория возникновения комплексных чисел

1. Развитие понятия о числе Древнегреческие математики считали “настоящими” только натуральные числа.

1. Развитие понятия о числе Введение отрицательных чисел - это было сделано

2. На пути к комплексным числамВ XVI веке в связи с изучением

В формуле для решения кубических уравнений вида:

Эта формула безотказно действует в случае, когда уравнение имеет один действительный корень,

Итальянский алгебраист Дж. Кардано в 1545 г. предложил ввести числа новой природы.

не имеющая решений во множестве действительных чисел, имеет решения вида

нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать что

3. Утверждение комплексных чисел в математике Кардано называл такие величины “чисто отрицательными”

Название “мнимые числа” ввел в 1637 году французский математик и философ Р.

Слово комплекс (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов,

Л. Эйлер вывел в 1748 году замечательную формулу

которая связывала воедино показательную функцию с тригонометрической. С помощью формулы Л.

В конце XVIII века французский математик Ж. Лагранж смог сказать, что математический

После создания теории комплексных чисел возник вопрос о существовании “гиперкомплексных” чисел

4.Геометрическое представление комплексного числа

Такая плоскость называется комплексной. Вещественные числа на ней занимают горизонтальную ось, мнимая

5. Тригонометрическая форма комплексного числа. Абсцисса а и ордината b комплексного числа

Комплексные числа, несмотря на их “лживость” и недействительность, имеют очень широкое применение.

Поэтому всякое комплексное число можно представить в виде r(cos

Слайды презентации

Слайд 2 1. Развитие понятия о числе
Древнегреческие математики считали “настоящими”

1. Развитие понятия о числе Древнегреческие математики считали “настоящими” только натуральные

только натуральные числа.
Наряду с натуральными числами применяли дроби

- числа, составленные из целого числа долей единицы.

Слайд 3 1. Развитие понятия о числе
Введение отрицательных чисел -

1. Развитие понятия о числе Введение отрицательных чисел - это было

это было сделано китайскими математиками за два века до

н. э.
Уже в VIII веке было установлено, что квадратный корень из положительного числа имеет два значения - положительное и отрицательное, а из отрицательных чисел квадратный корень извлекать нельзя.

Слайд 4 2. На пути к комплексным числам
В XVI веке

2. На пути к комплексным числамВ XVI веке в связи с

в связи с изучением кубических уравнений оказалось необходимым извлекать

квадратные корни из отрицательных чисел.

Слайд 5 В формуле для решения кубических уравнений вида:

Слайд 6 кубические и квадратные корни:

Слайд 7
Эта формула безотказно действует в случае, когда уравнение

Эта формула безотказно действует в случае, когда уравнение имеет один действительный

имеет один действительный корень, а если оно имеет три

действительных корня, то под знаком квадратного корня оказывалось отрицательное число. Получалось, что путь к этим корням ведет через невозможную операцию извлечения квадратного корня из отрицательного числа.

Слайд 8

x=1

Слайд 9

Кроме х=1, есть еще два корня

Слайд 10 Итальянский алгебраист Дж. Кардано в 1545 г. предложил

Итальянский алгебраист Дж. Кардано в 1545 г. предложил ввести числа новой

ввести числа новой природы. Он показал, что система уравнений

Слайд 11 не имеющая решений во множестве действительных чисел, имеет

решения вида

Слайд 12 нужно только условиться действовать над такими выражениями по

правилам обычной алгебры и считать что

Слайд 13 3. Утверждение комплексных чисел в математике
Кардано называл такие

3. Утверждение комплексных чисел в математике Кардано называл такие величины “чисто

величины “чисто отрицательными” и даже “софистически отрицательными”, считал их

бесполезными и старался их не употреблять.
Но уже в 1572 году вышла книга итальянского алгебраиста Р. Бомбелли, в которой были установлены первые правила арифметических операций над такими числами, вплоть до извлечения из них кубических корней.

Слайд 14
Название “мнимые числа” ввел в 1637 году французский

Название “мнимые числа” ввел в 1637 году французский математик и философ

математик и философ Р. Декарт.
В 1777 году один

из крупнейших математиков XVIII века - Л. Эйлер предложил использовать первую букву французского слова imaginaire (мнимый) для обозначения числа (мнимой единицы). Этот символ вошел во всеобщее употребление благодаря К. Гауссу . Термин “комплексные числа” так же был введен Гауссом в 1831 году.

Слайд 15
Слово комплекс (от латинского complexus) означает связь,

Слово комплекс (от латинского complexus) означает связь, сочетание, совокупность понятий,

сочетание, совокупность понятий, предметов, явлений и т. д. Образующих

единое целое.

Слайд 16 Л. Эйлер вывел в 1748 году замечательную формулу

Слайд 17
которая связывала воедино показательную функцию с тригонометрической.

которая связывала воедино показательную функцию с тригонометрической. С помощью формулы

С помощью формулы Л. Эйлера можно было возводить число

e в любую комплексную степень.

Слайд 18
В конце XVIII века французский математик Ж. Лагранж

В конце XVIII века французский математик Ж. Лагранж смог сказать, что

смог сказать, что математический анализ уже не затрудняют мнимые

величины.

Слайд 19 После создания теории комплексных чисел возник вопрос

После создания теории комплексных чисел возник вопрос о существовании “гиперкомплексных”

о существовании “гиперкомплексных” чисел - чисел с несколькими “мнимыми”

единицами. Такую систему построил в 1843 году ирландский математик У. Гамильтон, который назвал их “кватернионами”

Слайд 20

Слайд 21 4.Геометрическое представление комплексного числа

Слайд 22
Такая плоскость называется комплексной. Вещественные числа на ней

Такая плоскость называется комплексной. Вещественные числа на ней занимают горизонтальную ось,

занимают горизонтальную ось, мнимая единица изображается единицей на вертикальной

оси; по этой причине горизонтальная и вертикальная оси называются соответственно вещественной и мнимой осями.

Слайд 23 5. Тригонометрическая форма комплексного числа.
Абсцисса а и

5. Тригонометрическая форма комплексного числа. Абсцисса а и ордината b комплексного

ордината b комплексного числа a + bi выражаются через

модуль r и аргумент q. Формулами
a = r cos q , r=a/cos q
b = r sin q , r=b/sin q
r – длина вектора (a+bi) , q – угол, который он образует с положительным направлением оси абсцисс

Слайд 24 Комплексные числа, несмотря на их “лживость” и недействительность,

Комплексные числа, несмотря на их “лживость” и недействительность, имеют очень широкое

имеют очень широкое применение. Они играют значительную роль не

только в математике, а также в таких науках, как физика, химия. В настоящее время комплексные числа активно используются в электромеханике, компьютерной и космической индустрии

Слайд 25 Поэтому всякое комплексное число можно представить в виде

r(cos q + i sin

q),
где r > 0 т.е. z=a+bi или z=r*cos q + r*sin q
Это выражение называется нормальной тригонометрической формой или, короче, тригонометрической формой комплексного числа.