- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Квадрат суммы. Квадрат разности 7 класс
Содержание
- 2. Тема урока:Квадрат суммы. Квадрат разности.
- 3. Цель урока:Познакомиться с формулами квадрата суммы и
- 4. Задачи урока:1. Развивающая - познакомиться с более
- 5. УСТНЫЙ СЧЁТ:Возвести в квадрат:a; 4а;
- 6. УСТНЫЙ СЧЁТ:Найдите число, которое в квадрате даст
- 7. УСТНЫЙ СЧЁТ:Найдите удвоенное произведение выражений: a и
- 8. Сформулируйте правило умножения многочлена на многочлен?
- 9. Получаем ФОРМУЛУ КВАДРАТА СУММЫ(a+b)2 =a2+2ab+b2 Квадрат
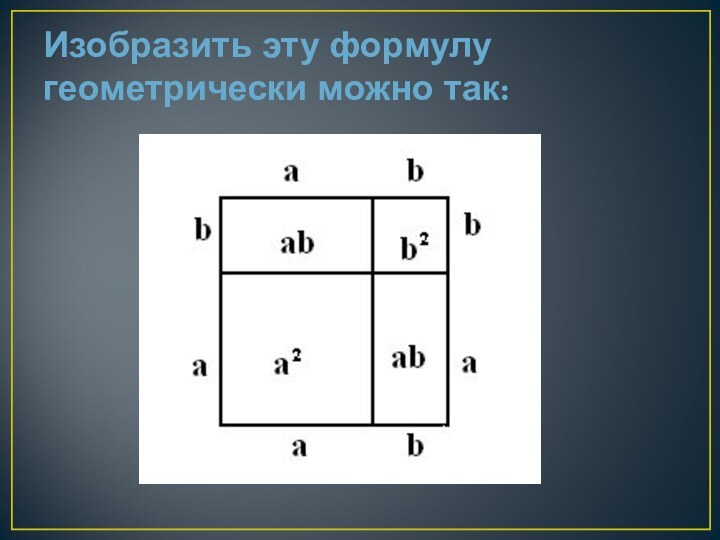
- 10. Изобразить эту формулу геометрически можно так:
- 11. ФОРМУЛА КВАДРАТА РАЗНОСТИ(a-b)2 =a2-2ab+b2 Квадрат разности
- 12. ВАЖНО! а и b в формулах могут быть любыми числами или алгебраическими выражениями
- 13. ФОРМУЛЫ СОКРАЩЁННОГО УМНОЖЕНИЯ:(a+b)2 =a2+2ab+b2(a-b)2 =a2-2ab+b2
- 14. Формулы сокращённого умножения применяются в некоторых случаях
- 15. Преобразуем выражение в виде многочлена:(2m+3k)² = (2m)2+2●2m●3k+(3k)2=4m2+12mk+9k2(5a2-3)² = (5a)2-2● 5a2●3+32=25a4 -30a2+9
- 16. Вылечи равенство:(a-2b)2= a2- *ab+4b2(2a+0,5b)2= 4a2+2ab+*b29d2- 12dc+*c2= (3d-2c)2(4k+2m)2= *k2+16km+4m2
- 17. Представить квадрат двучлена в виде многочлена:№3701) (c+d)² (x-y)² (2+x)²4) (x+1)²
- 18. РЕЗУЛЬТАТ:1) (c+d)² = c2+2cd+d22) (x-y)²
- 19. ВЫЧИСЛИТЬ:№374
- 20. РЕЗУЛЬТАТ:№374
- 21. Применив формулы, заполните таблицу:
- 22. Результаты:
- 23. Итоги урока:Что нового вы узнали сегодня на
- 24. Домашнее задание:§ 22 страницы 90-92. Прочитать и выучить словесные формулировки формул. № 379, №380.
- 25. Скачать презентацию
- 26. Похожие презентации
Тема урока:Квадрат суммы. Квадрат разности.
























Слайд 4
Задачи урока:
1. Развивающая - познакомиться с более легким
способом алгебраических вычислений, вывести формулы квадрата суммы и квадрата
разности двух чисел.2. Образовательная - приобрести навык вычисления по формулам квадрата суммы и квадрата разности двух чисел, учиться выявлять главные и определенные закономерности.
3. Воспитательная -осознать ценность и необходимость полученных знаний, сопереживать за достижения своих товарищей.
Слайд 5
УСТНЫЙ СЧЁТ:
Возвести в квадрат:
a; 4а;
3c; 8с²k³; 5с4k6 ; 10pd6
ОТВЕТЫ:
a2 ;
16а2; 9c2; 64с4 k6; 25с8k12 ; 100p2d12
Слайд 6
УСТНЫЙ СЧЁТ:
Найдите число, которое в квадрате даст
100;
25a2 ; 81х2у4 ;
49k6 d10ОТВЕТЫ:
10; 5a ; 9ху2 ; 7k3d5
Слайд 7
УСТНЫЙ СЧЁТ:
Найдите удвоенное произведение выражений:
a и b,
0,5c и 6,
4x и 2x²,
2b и -5kОтветы:
2ab, 3c, 8x3, -10 bk
Слайд 8
Сформулируйте правило умножения многочлена на многочлен?
Рассмотрим
квадрат суммы двух чисел (a+b)2 и пользуясь правилом умножения
многочлена на многочлен, получаем:(a+b)2 =(a+b)(a+b)= a2+ab+ab+b2 = a2+2ab+b2





























