ФОРМУЛ СОКРАЩЕННОГО УМНОЖЕНИЯ; РАЗВИВАТЬ ВНИМАНИЕ, ПАМЯТЬ, РЕЧЬ, ЛОГИЧЕСКОЕ МЫШЛЕНИЕ,
САМОСТОЯТЕЛЬНОСТЬ. ВОСПИТАТЬ СТРЕМЛЕНИЕ ДОСТИГНУТЬ ПОСТАВЛЕННУЮ ЦЕЛЬ, ЧУВСТВО ОТВЕТСТВЕННОСТИ, УВЕРЕННОСТИ В СЕБЕ, УМЕНИЕ РАБОТАТЬ В КОЛЛЕКТИВЕ. Цель урока:
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть






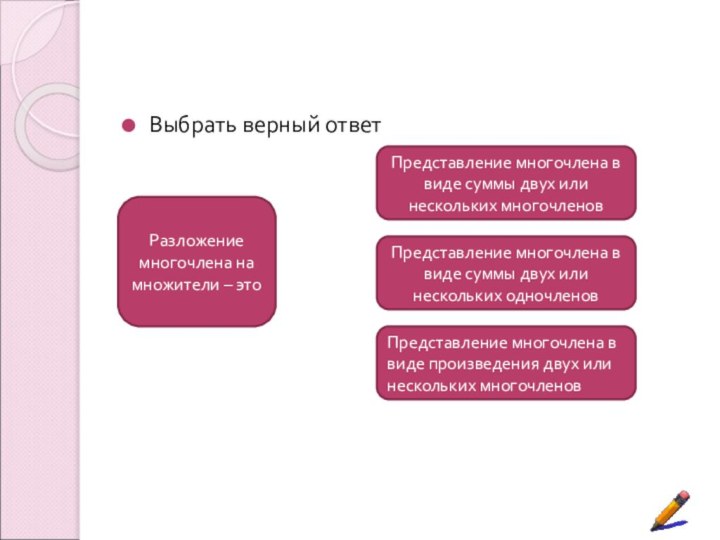
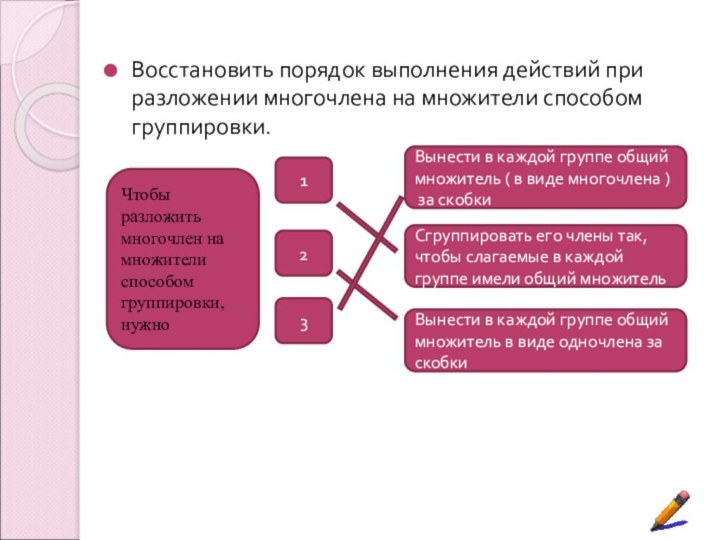
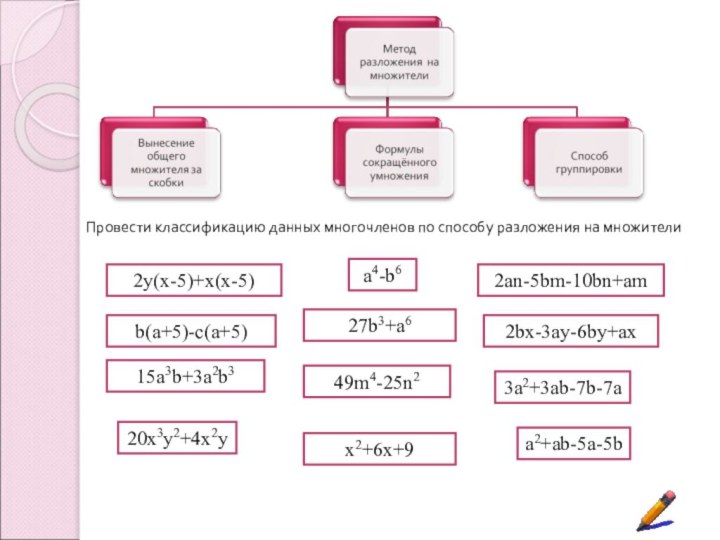
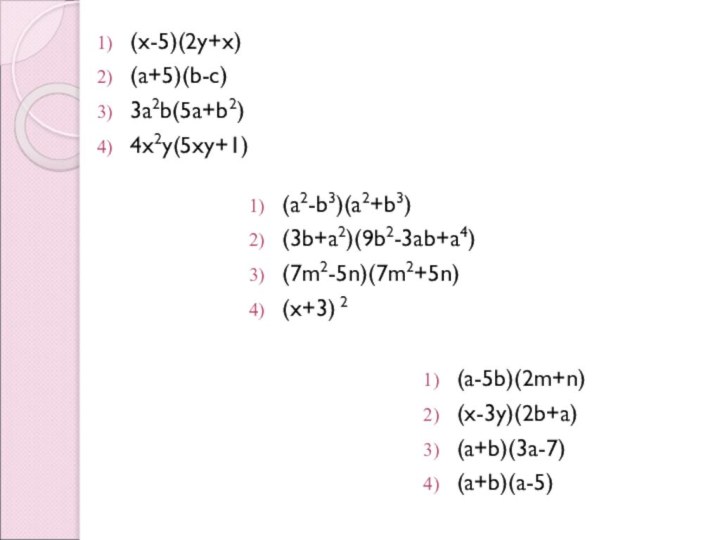















Цель урока:
+
-
-
+
-
-
Представление многочлена в виде произведения двух или нескольких многочленов
1
3
2
Вынести в каждой группе общий множитель ( в виде многочлена )
за скобки
Сгруппировать его члены так, чтобы слагаемые в каждой группе имели общий множитель
Вынести в каждой группе общий множитель в виде одночлена за скобки
x² + 4a²
x² - 2a²x + a
Текст слайда
Пирой: x
- 4xy + 4y
=
Стилбон: 4x
+ 4xy + y
=
Фаэтон: x
- 2x
y + y
=
Фенон: y
- 4xy
+4x
=
Эосфорос: 0,25x
+2xy +4y
=
+
x
+2xy=
Геспер: 4y
(0,5x + 2y) ²
(x -2y) ²
Текст слайда
Комбинировали два приема:
-вынесение общего множителя за скобки;
- использование формул сокращенного умножения.
ОТВЕТЫ
1. 10a+15c
2. 4a2-9b2
3. 6xy-ab-2bx-3ay
4. 4a2+28ab+49b2
5. b(a+c)+2a+2c
6. 5a3c-20acb-10ac
7. x2-3x-5x+15
8. 9a2-6ac+c2