- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Логические высказывания
Содержание
- 2. ЦЕЛЬРассмотреть основные понятия алгебры высказыванийрассмотреть основные логические операции алгебры логики и научиться ими пользоваться
- 3. ЛЕКЦИЯПОВТОРЕНИЕРассмотренные ранее понятия:ЛОГИКАФОРМЫ МЫШЛЕНИЯЗНАЧЕНИЯ ВЫСКАЗЫВАНИЙ
- 4. Термин «логика» происходит от древнегреческого logos –
- 5. Алгебра высказываний В алгебре высказываний высказывания
- 6. Основным объектом в логике является высказывание.Высказывание –
- 7. Примеры:Москва – столица РоссииСтудент математического факультета педагогического
- 8. Простые высказывания обозначают заглавными латинскими буквами A,
- 9. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ
- 10. Логическое умножение (конъюнкция, &)Объединение двух или нескольких
- 11. Логическое умножение (конъюнкция)Составное высказывание, образованное в результате
- 12. Таблица истинности функции логического умножения
- 13. ПРИМЕР1. А=«2*2=5»(ложь),В=«3*3=10»(ложь) F=А&В – ложь2.
- 14. Логическое сложение (дизъюнкция, V)Объединение двух или
- 15. Логическое сложение (дизъюнкция)Составное высказывание, образованное в результате
- 16. Таблица истинности функции логического сложения
- 17. ПРИМЕР1. А=«2*2=5»(ложь),В=«3*3=10»(ложь) F=АVВ – ложь2.
- 18. Логическое отрицание (инверсия)Присоединение частицы «НЕ» к высказыванию называется операцией логического отрицания или инверсией.
- 19. Логическое отрицание (инверсия)Логическое отрицание (инверсия) делает истинное высказывание ложным, и наоборот, ложное – истинным.
- 20. Таблица истинности функции логического отрицания
- 21. ПРИМЕР1. А=«Два умножить на два равно четырем»
- 22. Представлениесложных сужденийв виде формул
- 23. Пример 1Мы пойдем в театр и
- 24. ПРАКТИКАРешение задачКонспект стр.92 (импликация, эквиваленция)
- 25. ПРАКТИКА ЗАДАЧА 1 Выделите в составных высказываниях
- 26. ЗАДАЧА 2 Даны два простых высказывания:
- 27. ЗАДАЧА 3Вычислить значение логической формулы: (не Х
- 28. Скачать презентацию
- 29. Похожие презентации
























Слайд 2
ЦЕЛЬ
Рассмотреть основные понятия алгебры высказываний
рассмотреть основные логические операции
алгебры логики и научиться ими пользоваться
Слайд 4 Термин «логика» происходит от древнегреческого logos – «слово,
мысль, понятие, рассуждение, закон».
Логика является одной из дисциплин, образующих
математический фундамент информатики.В вычислительной технике и автоматике используются логические схемы – устройства, которые преобразуют двоичные сигналы.
Анализ и проектирование логических схем опираются на законы алгебры логики.
Любой язык программирования содержит логические переменные и средства для описания и вычисления логических выражений.
Логические методы применяются и при работе с базами данных.
Слайд 5
Алгебра высказываний
В алгебре высказываний высказывания обозначаются именами логических
переменных, которые могут принимать лишь два значения:
«истина» (1)
или «ложь» (0)
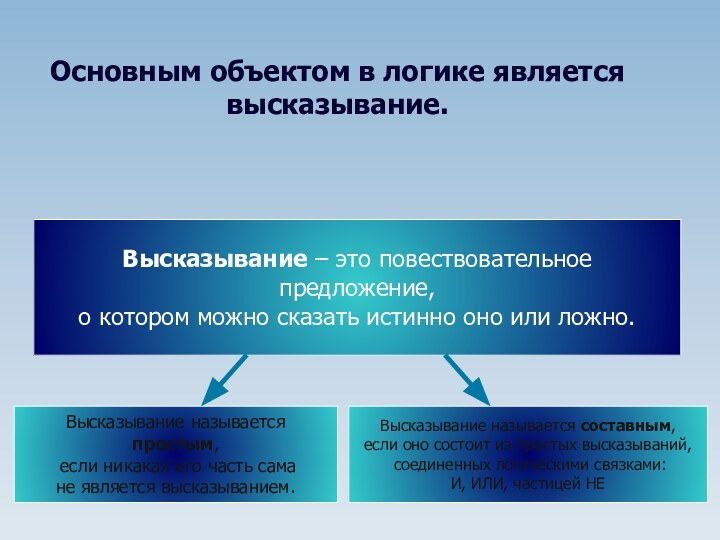
Слайд 6
Основным объектом в логике является высказывание.
Высказывание – это
повествовательное предложение,
о котором можно сказать истинно оно или
ложно.Высказывание называется простым,
если никакая его часть сама
не является высказыванием.
Высказывание называется составным,
если оно состоит из простых высказываний,
соединенных логическими связками:
И, ИЛИ, частицей НЕ
Слайд 7
Примеры:
Москва – столица России
Студент математического факультета педагогического университета
Треугольник
АВС подобен треугольнику А’В’С’
Луна есть спутник Марса
Кислород – газ
Каша
– вкусное блюдоМатематика – интересный предмет
Железо тяжелее свинца
Треугольник называется равносторонним, если все его стороны равны
Сегодня плохая погода
Река Ангара впадает в озеро Байкал
Какие из этих предложений являются высказываниями?
Ответ: 1, 4, 5, 8, 9, 11
Слайд 8
Простые высказывания обозначают
заглавными латинскими буквами
A, B,
C…X, Y, Z и называют
логическими переменными
Значения высказываний
ИСТИНА или
ЛОЖЬ обозначаютсоответственно цифрами 1 и 0
и называют логическими величинами
Составные высказывания называются
логическими выражениями и включают
в себя логические переменные,
операции логики и скобки для изменения
порядка действий операций
Слайд 10
Логическое умножение (конъюнкция, &)
Объединение двух или нескольких высказываний
в одно с помощью союза «И» называется операцией логического
умножения или конъюнкцией.
Слайд 11
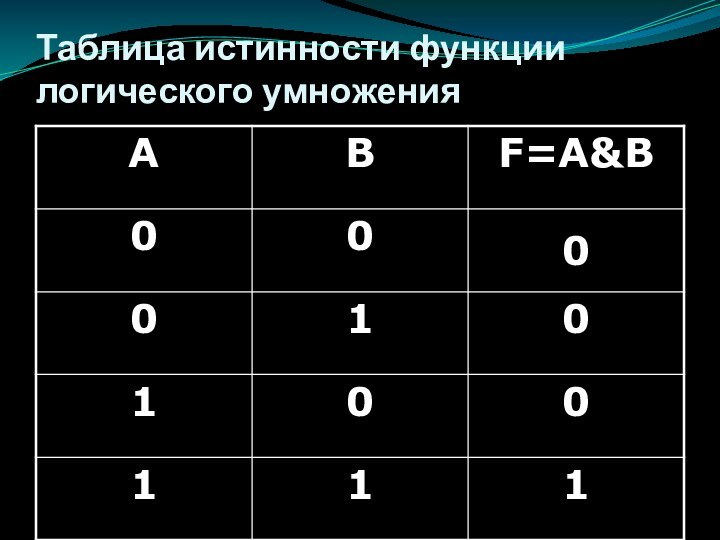
Логическое умножение (конъюнкция)
Составное высказывание, образованное в результате логического
умножения или конъюнкции, истинно тогда и только тогда, когда
истинны все входящие в него простые высказывания
Слайд 13
ПРИМЕР
1. А=«2*2=5»(ложь),В=«3*3=10»(ложь)
F=А&В – ложь
2. А=«2*2=4»(истина),В=«3*3=6»(ложь)
F=А&В – ложь
3. А=«2*2=4»(истина),В=«3*3=9»(ист.)
F=А&В
– истина4. Все гуси – птицы и Все игрушки – машины F=?
Слайд 14
Логическое сложение
(дизъюнкция, V)
Объединение двух или нескольких высказываний
с помощью союза «ИЛИ» называется логическим сложением или дизъюнкцией.
Слайд 15
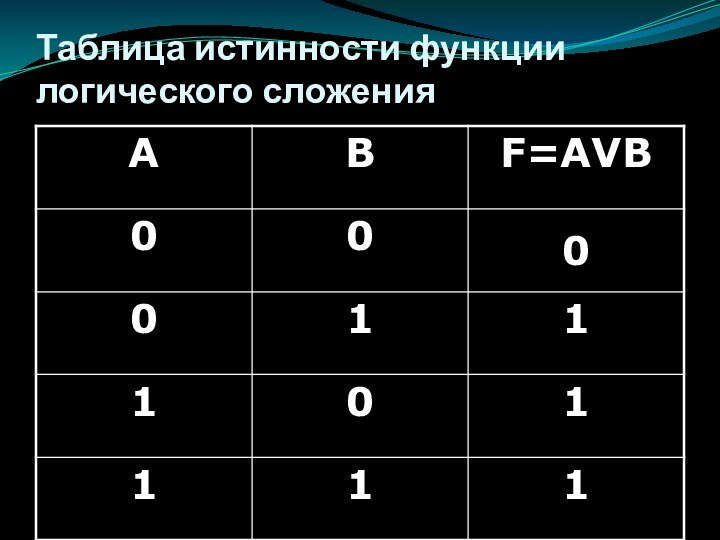
Логическое сложение (дизъюнкция)
Составное высказывание, образованное в результате логического
сложения, истинно тогда, когда истинно хотя бы одно из
входящих в него простых высказываний.
Слайд 17
ПРИМЕР
1. А=«2*2=5»(ложь),В=«3*3=10»(ложь)
F=АVВ – ложь
2. А=«2*2=4»(истина),В=«3*3=6»(ложь)
F=АVВ – истина
3. А=«2*2=4»(истина),В=«3*3=9»(ист.)
F=АVВ
– истина4. 2 * 2 = 4 или Белые медведи живут в Африке F=?
Слайд 18
Логическое отрицание (инверсия)
Присоединение частицы «НЕ» к высказыванию называется
операцией логического отрицания или инверсией.
Слайд 19
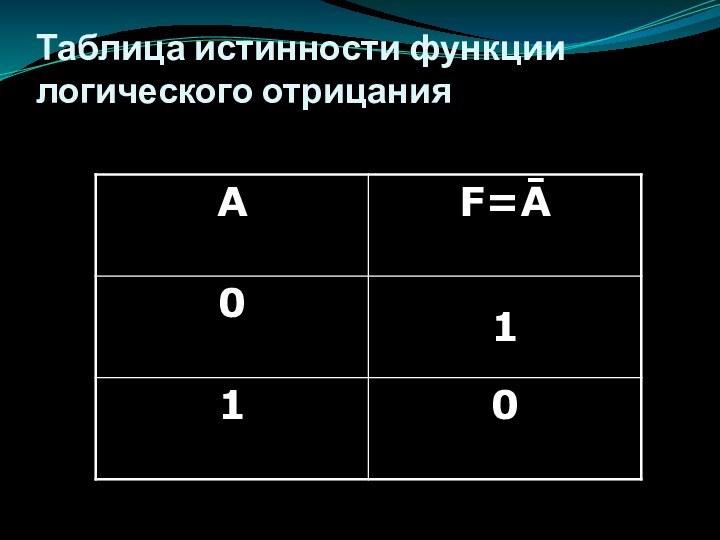
Логическое отрицание (инверсия)
Логическое отрицание (инверсия) делает истинное высказывание
ложным, и наоборот, ложное – истинным.
Слайд 21
ПРИМЕР
1. А=«Два умножить на два равно четырем»
F=Ā ложь
2. А=«Два умножить на два равно
четырем» F=А истина
Слайд 23
Пример 1
Мы пойдем в театр и будем
смотреть балет или пойдем в цирк и посмотрим представление.
Это
сложное логическое выражение состоит из четырех простых.А=«Мы пойдем в театр»
В=«Мы будем смотреть балет».
С=«Мы пойдем в цирк».
D=«Мы посмотрим представление».
Запись сложного логического выражения с помощью формулы
X=A*B+C*D
X=A&BVC&D
Слайд 25
ПРАКТИКА
ЗАДАЧА 1
Выделите в составных высказываниях простые. Обозначьте
каждое их них буквой; запишите с помощью
логических операций каждое составное высказывание.1) Число 376 четное и трехзначное.
2) Неверно, что Солнце движется вокруг Земли.
Слайд 26
ЗАДАЧА 2
Даны два простых высказывания:
А
= {2 * 2 = 4}, В = {2
* 2 = 5}.Какие из составных высказываний истинны:
а) Ā;
б) не B;
в) А & В;
г) A V В.
Слайд 27
ЗАДАЧА 3
Вычислить значение логической формулы:
(не Х и
У) или (Х и Z), если логические переменные имеют
следующие значения: Х=0, У=1, Z=1Решение. Отметим цифрами сверху порядок выполнения операций в выражении:
не 0=1
1 и 1= 1
0 и 1 =0
1 или 0 =1
ОТВЕТ: 1





























