- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Методы решения уравнений и неравенств
Содержание
- 2. Гипотеза работы Существует большое количество способов
- 3. Цели работыИзучить нестандартные методы решения уравнений и
- 4. Древний Египет«Фальфивое правило»Задача: куча. Ее седьмая часть 19. Найти кучуБудет хорошо
- 5. ВавилонДиофант (жил предположительно в III веке н.
- 6. Задача № 80Задача: Найти 2 таких числа,
- 7. Кубические уравненияАрхимед (287 до н. э. —
- 8. Решение уравнений с модулем1.«Сравнение модулей»
- 9. Сравнение квадратов │x - 1│= 2
- 10. Введение новой переменной + раскрытие модуля на
- 11. Раскрытие модуля на интервалах
- 12. Использование свойства четности
- 13. Графический способ решения уравнений, содержащих модуль|4 –
- 14. Уравнения с параметрамиУравнение с параметрами – математическое
- 15. Задача: При каких
- 16. Шаг 1Функция y=x2-(a+1)x+2a2График этой функции - парабола, ветви направлены вверх
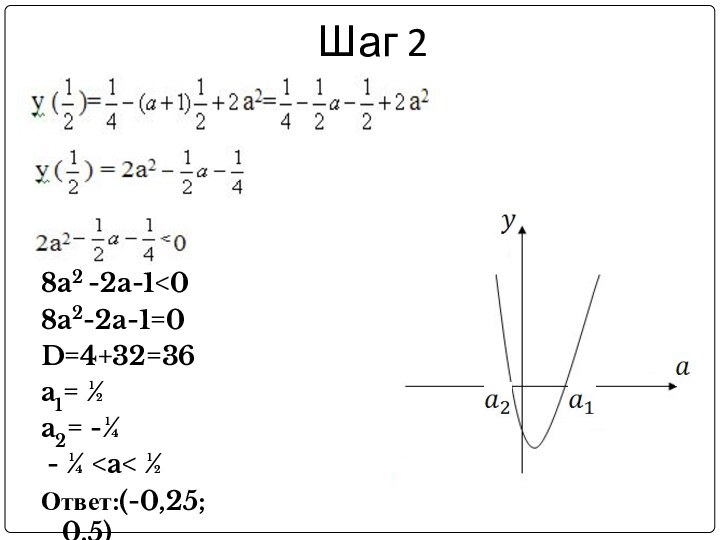
- 17. Шаг 28a2 -2a-1
- 18. Задача: При каких
- 19. 1 способ,,;;
- 20. 2 способГрафик первого уравнения - окружность с
- 21. Схема ГорнераДелим уравнение на (x-1)Пример:Делим уравнение на (x-2)Решаем квадратное уравнение, x=3 и x=4Ответ: 1;2;3;4
- 22. Формулы Виета
- 23. Решение с выделением полного квадратаПример: x4 –
- 24. Разделим обе части уравнения на; или Ответ: Пусть , тогда получимкорней нет Идея однородностиПример:,
- 25. Решение уравнений относительно коэффициентовили ; Определяем коэффициенты и решаем квадратное уравнение: ;;Пример:+
- 26. Ответ: 2 квадратных уравнения;корней нет; - посторонний корень
- 27. Ответ: Метод разложения на простейшие дробиВыделяем из числителя 1 и переносим:
- 28. Неравенство треугольника (Евклидова геометрия)Внешний угол больше внутреннего,
- 29. Неравенство Коши
- 30. Из всех равновеликих
- 31. Неравенства с модулем Соотношение двух величин,
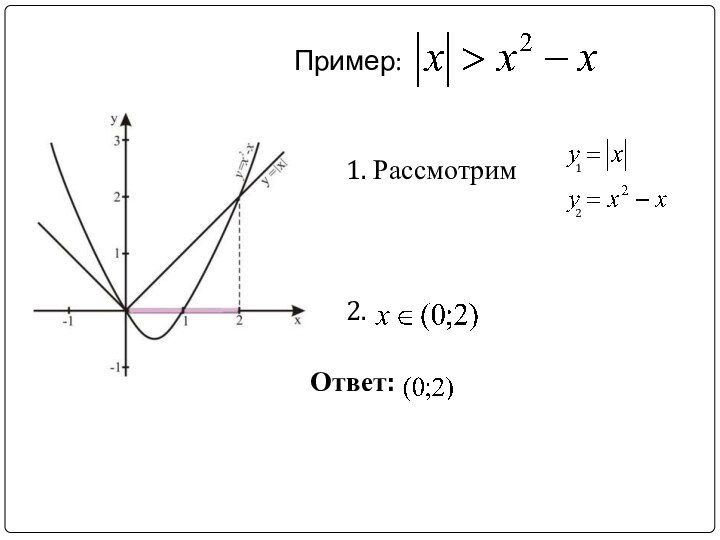
- 32. Пример: 1. Рассмотрим 2. Ответ:12
- 33. Пример:Если дискриминанты положительны, топриD/4=4+5+a=a+9D/4=4+5-a=9-aОтвет: (0;9)
- 34. Пример:Ответ:|3х - 1| - |х - 1|<
- 35. Неравенства с параметрами Неравенство
- 36. Пример: Ответ:Для всех допустимых значений параметра а решить неравенство: ;;;;;
- 37. Задача: Найдите все значения а при которых
- 39. y=2x+8y=2x+8;;;;;
- 40. Ответ: при исходное неравенство не содержит ни одного решения неравенства
- 41. Метод “Ромашки”f(х) = -натуральные числаf(х) >0 (соответственно
- 42. (х + 1)(х — 2) 2 >
- 43. ≥0Пример:Ответ: (0; 3] {7}.Рассмотрим функцию f(x)=х≠0. х≠4Нули функции: х=3, х=7
- 44. ЗаключениеМы поставили перед собой задачи:Изучить нестандартные методы
- 45. Скачать презентацию
- 46. Похожие презентации




































![Методы решения уравнений и неравенств ≥0Пример:Ответ: (0; 3] {7}.Рассмотрим функцию f(x)=х≠0. х≠4Нули функции: х=3, х=7](/img/tmb/12/1130051/f2dd22920ac9f1deda096e359212a68e-720x.jpg)


Слайд 3
Цели работы
Изучить нестандартные методы решения уравнений и неравенств
Научиться
использовать их на практике
Создать наглядную и понятную презентацию для
ознакомительных целейОзнакомить класс с этими методами при помощи наглядных примеров
Создать папку с материалами работы
Слайд 5
Вавилон
Диофант (жил предположительно в III веке н. э.)
Квадратные
уравнения
Задача: Найти два числа, зная, что их сумма равна
20, а произведение — 96x = 2
= 12 и = 8
Слайд 6
Задача № 80
Задача: Найти 2 таких числа, чтобы
сумма квадрата каждого из них с другим искомым числом
дала полный квадратРешение:
s2 + 2s + 1 = (s + 1)2,
(2s + I)2 + s ,
4s2 + 5s + 1 = t2 ,
Положим, что:
t = 2s — 2 ,
t2 = 4s2 — 8s + 4 = 4s2 + 5s + 1,
4s2 — 8s + 4 = 4s2 + 5s + 1.
Проверка:
Слайд 7
Кубические уравнения
Архимед (287 до н. э. — 212
до н. э.)
Сочинение: «О шаре и цилиндре»
Задача: рассечь
заданный отрезок а на две части х и а—х так, чтобы
(а — х) : с = S : х2
Слайд 8
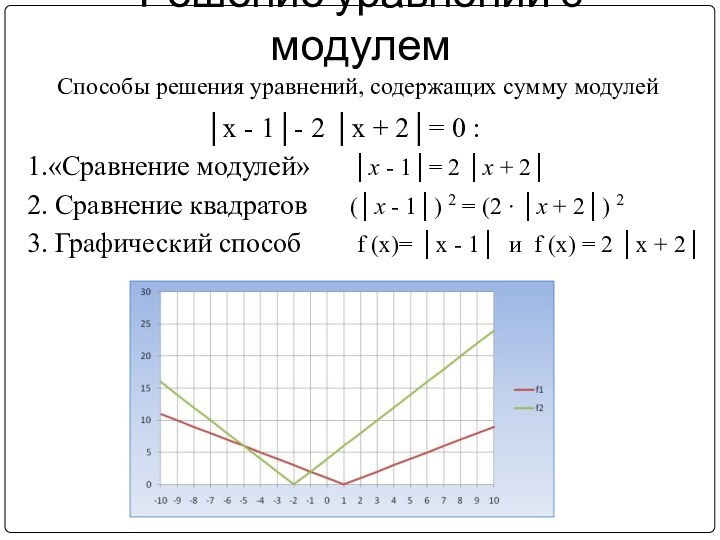
Решение уравнений с модулем
1.«Сравнение модулей» │x
- 1│= 2 │x + 2│
2. Сравнение квадратов
(│x - 1│) 2 = (2 ∙ │x + 2│) 2 3. Графический способ f (x)= │x - 1│ и f (x) = 2 │x + 2│
Способы решения уравнений, содержащих сумму модулей
│x - 1│- 2 │x + 2│= 0 :
Слайд 9
Сравнение квадратов
│x - 1│= 2 │x +
2│
(│x - 1│) 2 = (2 ∙
│x + 2│) 2 (х – 1) 2 - ( 2х + 4) 2 = 0
((х – 1) - ( 2х + 4)) ∙ ((х – 1) + ( 2х + 4)) = 0
(х – 1 - 2х - 4) ∙ (х – 1 + 2х + 4) = 0
х – 1 - 2х – 4 = 0 или х – 1 + 2х + 4 = 0
- х - 5 = 0 3х + 3 = 0 x = - 5 x = - 1
Пример:
Ответ:-5;-1
Слайд 10
Введение новой переменной + раскрытие модуля на интервалах
│4 |x |+ 5│= 6|x |
| x |= a,
где a > 0, тогда | 4а+5 |=6а4а+5 =-6а 4а+5 =6а
Не удовлетворяет условию а>0
, значит,
Ответ:
Пример:
Слайд 11 Раскрытие модуля на интервалах (
начиная с внутреннего)
На промежутке
На промежутке
Не удовлетворяет условию
Не удовлетворяет условию
│4 |x |+ 5│= 6|x |
Пример:
Ответ:
Слайд 12
Использование свойства четности
у=│4 |x |+ 5│= 6|x |
.
4х + 5 = 6х и 4х + 5 = - 6х
Пример:
Ответ:
Слайд 13
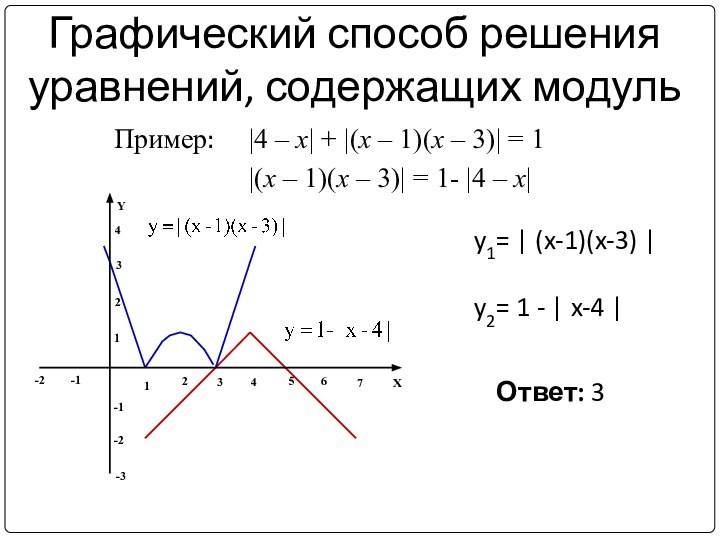
Графический способ решения уравнений, содержащих модуль
|4 – x|
+ |(x – 1)(x – 3)| = 1
Ответ:
3y1= | (x-1)(x-3) |
y2= 1 - | x-4 |
|(x – 1)(x – 3)| = 1- |4 – x|
Пример:
Слайд 14
Уравнения с параметрами
Уравнение с параметрами – математическое уравнение,
внешний вид и решение которого зависит от значений одного
или нескольких параметров.Способы решения:
Графический
Аналитический
Слайд 15
Задача:
При каких значениях
a один корень квадратного уравнения
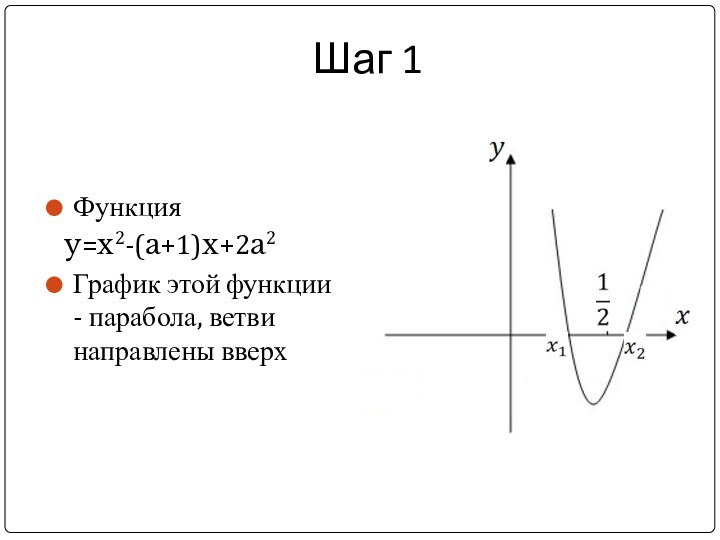
x2-(a+1)x+2a2=0 больше
, а другой меньше ?
Слайд 20
2 способ
График первого уравнения - окружность с центром
в начале координат и радиусом 3.
График второго уравнения
- прямаяF
,
;
Слайд 21
Схема Горнера
Делим уравнение на (x-1)
Пример:
Делим уравнение на (x-2)
Решаем
квадратное уравнение, x=3 и x=4
Ответ: 1;2;3;4
Слайд 22
Формулы Виета
Найти
кубическое уравнение, корни которого являются квадратами корней уравнения
Обозначим
корни искомого кубического уравнения какОтвет:
Задача:
Слайд 23
Решение с выделением полного квадрата
Пример: x4 – 2x3
– 3x2 + 4x + 4 = 0.
Представим –
3x2 как (x2 – 4x2)x4 – 2x3 + x2 – 4x2 + 4x + 4 = 0
Свернем по формуле и вынесем общий множитель
(x2 – x)2 – 4(x2 – x) + 4 = 0
Введем замену y = (x2 – x)
Решим уравнение, y=2
2= (x2 – x)
x=-1 или x=2
Ответ: -1;2
Слайд 24
Разделим обе части уравнения на
;
или
Ответ:
Пусть
,
тогда получим
корней нет
Идея однородности
Пример:
,
Слайд 25
Решение уравнений относительно коэффициентов
или
;
Определяем коэффициенты и
решаем квадратное уравнение:
;
;
Пример:
+
Слайд 28
Неравенство треугольника
(Евклидова геометрия)
Внешний угол больше внутреннего, с ним
не смежного
Против большей стороны лежит больший внутренний угол
Против большего
внутреннего угла лежит большая сторона
Слайд 30
Из всех равновеликих треугольников
найти треугольник наименьшего периметра.
Пусть x, y, z– стороны треугольника,
тогда:Применим неравенство Коши:
Наименьшее значение периметра равно
Достигается при x=y=z
Задача:
Слайд 31
Неравенства с модулем
Соотношение двух величин, одна
из который имеет модуль, показывающее, что одна величина больше
или меньше другой.Методы решения:
Метод промежутков
Графический
Слайд 34
Пример:
Ответ:
|3х - 1| - |х - 1|< 10
1
3
1
1
х
x
= 0;
-(3х - 1) + (х - 1)
<10x = -5;
( )
-5 ;
1
3
x = 0,5;
(3x - 1) + (x - 1) < 10;
4x < 12;
x < 3;
[ ]
1
3
; 1
( )
-5 ;
1
3
1
3
; 1
[ ]
x = 2;
(3x - 1) – (x - 1) < 10;
x < 5;
(1 ; 5)
(1 ; 5)
(-5 ; 5)
Слайд 35
Неравенства с параметрами
Неравенство
f
(a,b,c,…k,x) > ϕ (a,b,c,…k,x),
где a,b,c,…k – параметры,
а x –действительная переменная величина, называется неравенством с одним неизвестным, содержащим параметры.Слайд 37 Задача: Найдите все значения а при которых неравенство
не имеет решений
Ответ: (1;5)
График – парабола, ветви вверх
Слайд 38
Найти
все значение параметра q, при каждом из которых множество
решений неравенства не содержит ни одного решения неравенства
Задача:
Слайд 42
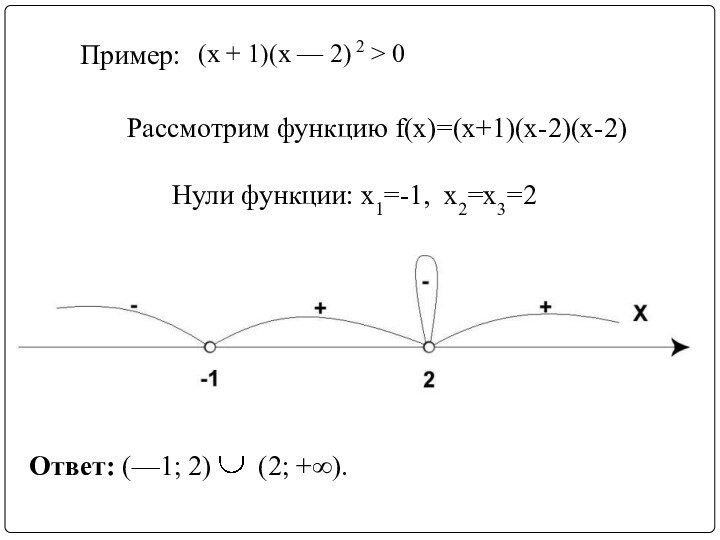
(х + 1)(х — 2) 2 > 0
Пример:
Ответ:
(—1; 2)
(2; +∞).
Рассмотрим функцию f(x)=(x+1)(x-2)(x-2)
Нули функции: х1=-1,
х2=х3=2
Слайд 44
Заключение
Мы поставили перед собой задачи:
Изучить нестандартные методы решения
уравнений и неравенств
Научиться использовать их на практике
Создать наглядную и
понятную презентацию для ознакомительных целейОзнакомить класс с этими методами при помощи наглядных примеров
Создать папку с материалами работы
Считаем, что намеченные нами цели достигнуты.





























