- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Математическая графика (11 класс)
Содержание
- 2. Математика и живопись.В искусстве существует математическая теория
- 6. «Там, где красота, там действуют законы математики». (Г.Х.Харди)
- 7. Эстетика геометрической формы, в частности эстетика линии,
- 8. Даже создать красивый танец невозможно без графиков
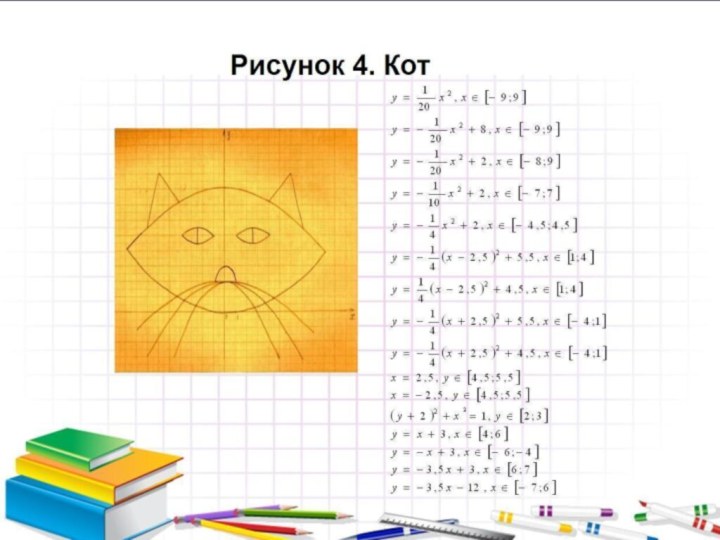
- 10. Метод «математической графики» использует построение графика функции и его преобразований в комплексе.
- 18. Построим пошагово рисунок 7 (гриб). Построим график
- 19. В этой же системекоординат построиманалогично графикфункции для
- 20. Продолжим наше построение. y= 1/20(x- ½ )2
- 21. Шляпка гриба ужеготова. Приступим кпостроению ножки. y= -7x+13 – прямая,где x принадлежит[1;2].
- 22. Аналогично построим прямую y=7x+6 , где xПринадлежит промежутку [-1; 0].
- 23. Остался последний шаг –основание гриба (этопарабола). Построимграфик
- 24. Нестандартный подход к изучению темы «Графики функции»,
- 26. Скачать презентацию
- 27. Похожие презентации
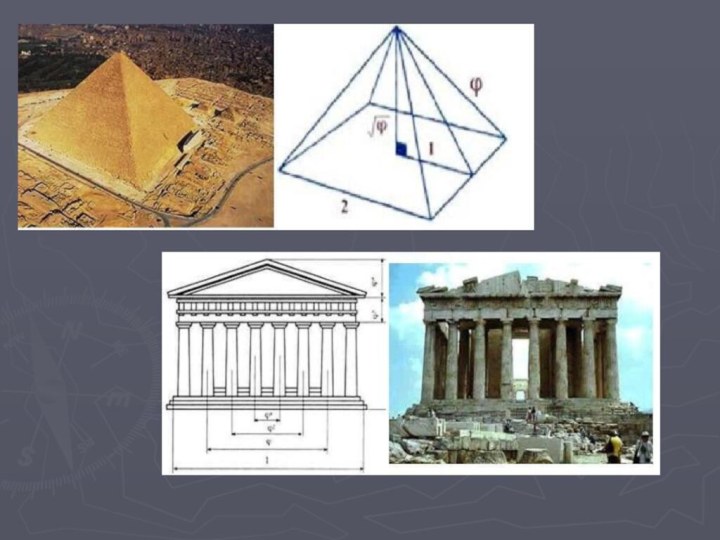
Математика и живопись.В искусстве существует математическая теория живописи. Это теория перспективы, по словам Леонардо до Винчи, «тончайшее исследование и изобретение, основанное на изучении математики, которое силою линий заставляло казаться отдаленным то, что близко, и большим то,

















![Математическая графика (11 класс) Шляпка гриба ужеготова. Приступим кпостроению ножки. y= -7x+13 – прямая,где x принадлежит[1;2].](/img/tmb/6/570909/c29c2fe0c73642b8570b1aa9e2b2c467-720x.jpg)
![Математическая графика (11 класс) Аналогично построим прямую y=7x+6 , где xПринадлежит промежутку [-1; 0].](/img/tmb/6/570909/848732b4f14d1c3ec3bfe0a73739dd35-720x.jpg)




Слайд 7 Эстетика геометрической формы, в частности эстетика линии, привлекала
к себе внимание не только математиков. При этом красоту
линии авторы обычно ставят в зависимость от сложности закона, по которому она строится или который она выражает.Слайд 8 Даже создать красивый танец невозможно без графиков математических
функций. Красивый танец - это красивый график. Все движения
танцоров подчиняются строгой гармонической линии.Слайд 10 Метод «математической графики» использует построение графика функции и
его преобразований в комплексе.
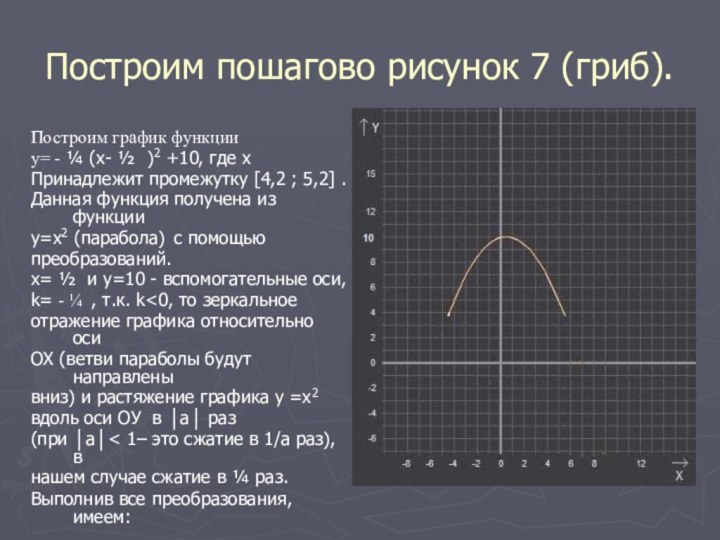
Слайд 18
Построим пошагово рисунок 7 (гриб).
Построим график функции
y= - ¼ (x- ½ )2 +10, где x
Принадлежит
промежутку [4,2 ; 5,2] .Данная функция получена из функции
y=x2 (парабола) с помощью
преобразований.
x= ½ и y=10 - вспомогательные оси,
k= - ¼ , т.к. k<0, то зеркальное
отражение графика относительно оси
ОХ (ветви параболы будут направлены
вниз) и растяжение графика y =x2
вдоль оси ОУ в │а│ раз
(при │а│< 1– это сжатие в 1/a раз), в
нашем случае сжатие в ¼ раз.
Выполнив все преобразования, имеем:
Слайд 19
В этой же системе
координат построим
аналогично график
функции для
y=
-1/20(x- ½)2 +6, где x так
же принадлежит промежутку
[-4,2; 5,2].
x=1/2 и y=6 – вспомогательные оси, а
сжатие в 1/20 раз. Выполнив
преобразования, получим:
Слайд 20
Продолжим наше
построение.
y= 1/20(x- ½ )2 +3,8.
Где
x уже принадлежит
промежутку [-4,2;-0,3] и
[-1,3; 5,2]. Здесь
вспомогательные оси:
x=
½ и y=3,8, сжатие в1/20 раз. Причем k>0,
значит ветви параболы
направлены вверх!
Получим:
Слайд 21
Шляпка гриба уже
готова. Приступим к
построению ножки.
y= -7x+13
– прямая,
где x принадлежит
[1;2].
Слайд 23
Остался последний шаг –
основание гриба (это
парабола). Построим
график функции
y= ½ (x- ½)2 -2, где x= ½,
y= -2 – вспомогательные
оси, а сжатие в ½ раз.
x принадлежит
промежутку [-1;2].
Выполнив все
преобразования,получим