- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему: логарифмическая функция
Содержание
- 2. Работа устно:НЕПРЕ
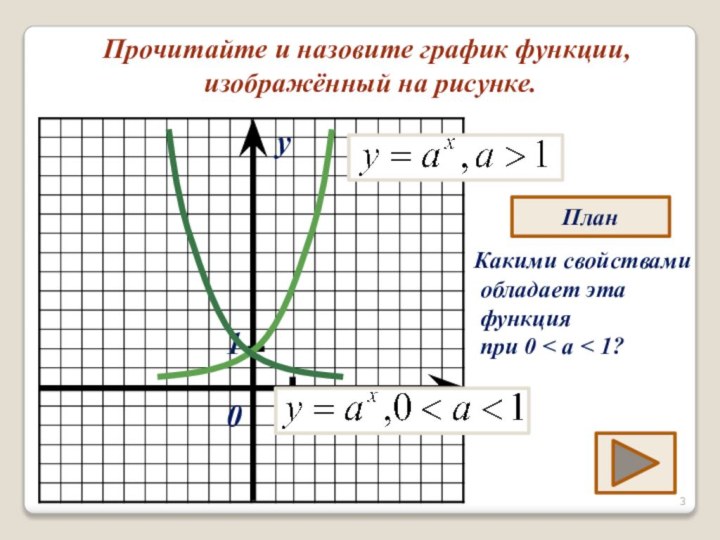
- 3. Прочитайте и назовите график функции, изображённый на
- 4. xy0cbcby = xПоказательная функцияЛогарифмическая функция(c ; b)
- 5. xy0aay = x11 График функции
- 6. xyy = x110 График функции
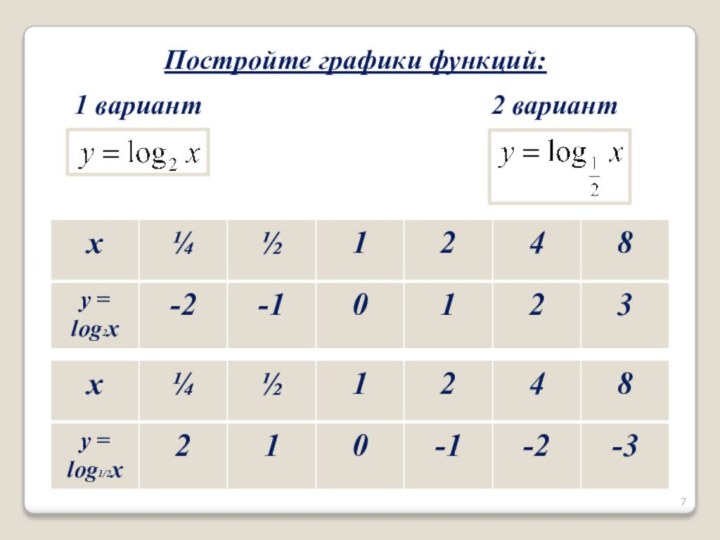
- 7. Постройте графики функций:1 вариант2 вариант
- 8. xy01231248- 1- 2- 3Проверка:График логарифмическойфункции называютлогарифмической кривой.
- 9. xy01231248- 1- 2График функции y = loga
- 10. 1) D(f) = (0, + ∞);2) не
- 11. 1) D(f) = (0, + ∞);2) не
- 12. Задание №1Найдите наибольшее и наименьшее значения функции
- 13. Задание №2Решите уравнение и неравенства:xy011- 1 Ответ:
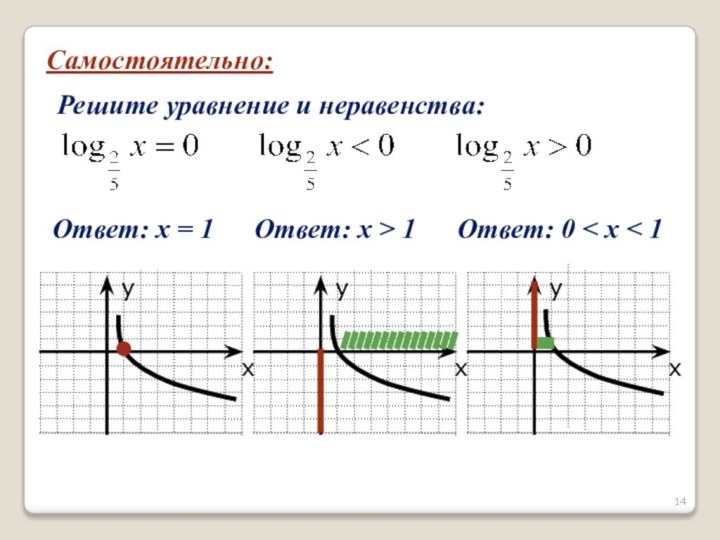
- 14. Самостоятельно:Решите уравнение и неравенства:Ответ: х = 1Ответ: х > 1Ответ: 0 < х < 1
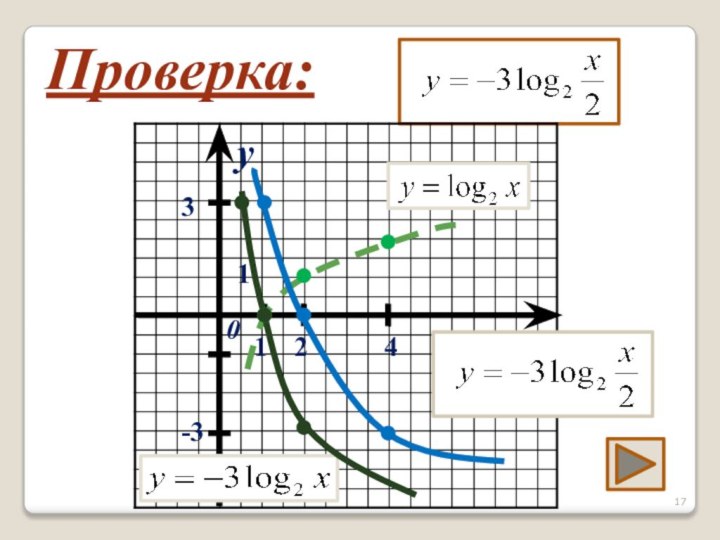
- 15. Задание №3Постройте графики функций:xy011y = - 3 x = - 2Самостоятельно.
- 16. xy011 Проверка:
- 17. Проверка:xy011 24-33
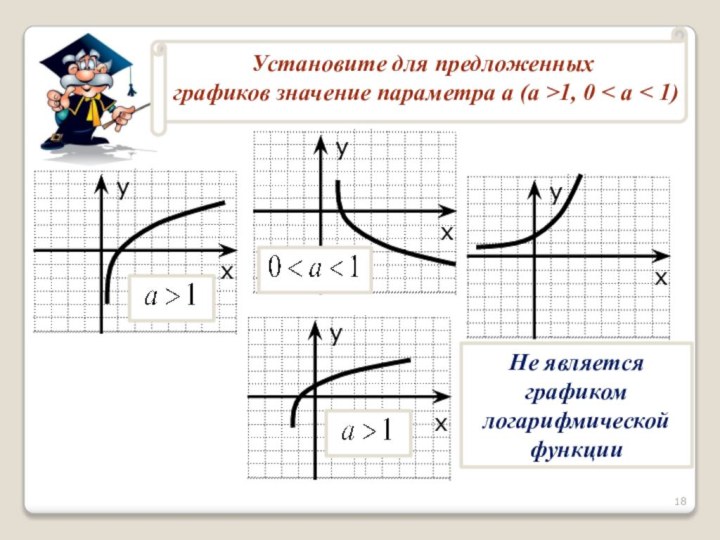
- 18. Не является графиком логарифмической функции
- 19. Ось у является вертикальной асимптотой графика логарифмической
- 20. Логарифмическая кривая это та же экспонента, толькопо
- 21. § 49 №1463, 1467,1480,14601 вариант – а,б;2 вариант – в,г.
- 22. Скачать презентацию
- 23. Похожие презентации
















Слайд 4
x
y
0
c
b
c
b
y = x
Показательная функция
Логарифмическая функция
(c ; b)
Если
точка (с;b)
принадлежит
показательной
функции, то
Или, на
«языкелогарифмов»
Что можно сказать
о точке (b;c)?
(b ; c)
Вывод:
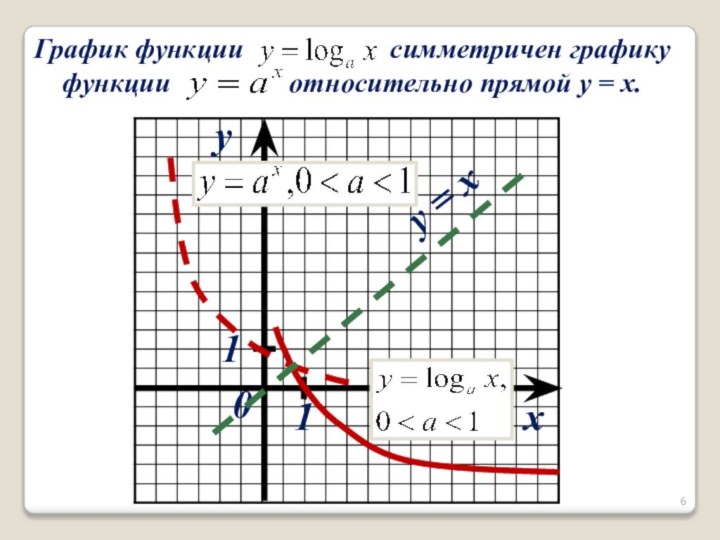
Слайд 9
x
y
0
1
2
3
1
2
4
8
- 1
- 2
График функции y = loga x.
Опишите
свойства
логарифмической
функции.
1 вариант:
при a > 1
2
вариант: при 0 < a < 1
Слайд 10
1) D(f) = (0, + ∞);
2) не является
ни чётной,
ни нечётной;
3) возрастает на (0, +
∞); 4)не ограничена сверху, не ограничена снизу;
5)не имеет ни наибольшего, ни наименьшего
значений;
6) непрерывна;
7) E(f) = (- ∞, + ∞);
8) выпукла вверх.
Слайд 11
1) D(f) = (0, + ∞);
2) не является
ни чётной,
ни нечётной;
3) убывает на (0, +
∞); 4)не ограничена сверху, не ограничена снизу;
5)не имеет ни наибольшего, ни наименьшего
значений;
6) непрерывна;
7) E(f) = (- ∞, + ∞);
8) выпукла вниз.
Слайд 12
Задание №1
Найдите наибольшее и наименьшее значения
функции на
промежутке:
Функция возрастает,
значит: yнаим.= lg1 = 0
yнаиб. =
lg1000 = lg10³ = 3Функция убывает,
значит: yнаим.= -3
yнаиб. = 2
Слайд 19
Ось у является вертикальной асимптотой графика
логарифмической
функции.
Графики показательной и логарифмической функций
симметричны относительно прямой у
= х.Область определения логарифмической функции – вся
числовая прямая, а область значений этой функции –
промежуток (0, + ∞).
Монотонность логарифмической функции зависит от
основания логарифма.
Не каждый график логарифмической функции проходит
через точку с координатами (1;0).
Слайд 20
Логарифмическая кривая это та же экспонента, только
по -
другому расположенная в координатной плоскости.
Выпуклость логарифмической функции не зависит
от основания логарифма.
Логарифмическая функция не является ни чётной, ни
нечётной.
Логарифмическая функция имеет наибольшее значение
и не имеет наименьшего значения при a >1 и наоборот
при 0 < a < 1.
Проверка:
Да, да, нет, да, нет, да, нет, да, нет





























