Презентация на тему Первообразная

на заданном промежутке, если для всех x из этого

F(x) = x3/3 есть первообразная для функции f(x)=x2 на интервале (-∞; ∞), так как

F′(x) = (x3/3)′ = 1/3(x3)′ = 1/3*3x2 = x2 = f(x)

для всех x ∈ (-∞; ∞).

Пример:

промежутке I может быть записана в виде
F(x) + C,
Где

Признак постоянства функции

Если F′(x) = 0 на некотором промежутке I, то функция F – постоянная на этом промежутке.

получим первообразную для функции f на промежутке I.

Какую бы

График двух любых первообразных для функции получается путем параллельного переноса вдоль оси OY.

так как (-x4/4)′ = -x3

Общий вид первообразной:
F(x) = -x4/4

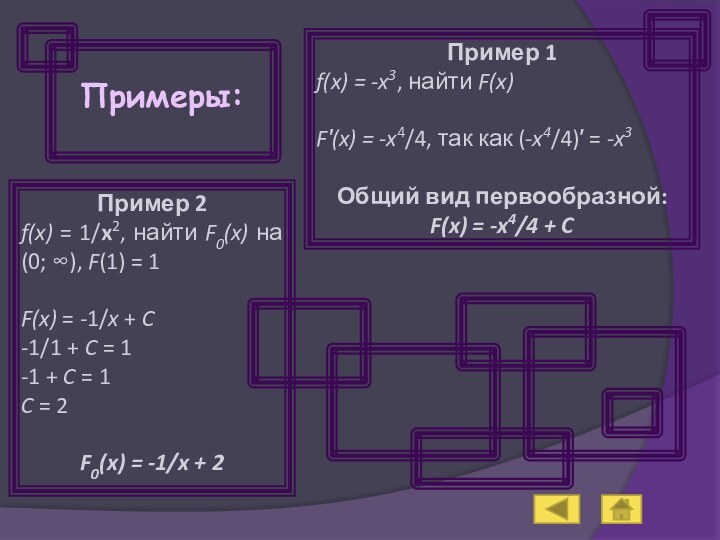
Пример 2
f(x) = 1/x2, найти F0(x) на (0; ∞), F(1) = 1

F(x) = -1/x + C
-1/1 + C = 1
-1 + C = 1
C = 2

F0(x) = -1/x + 2

для f, а G – первообразная для g, то

Пример
f(x) = x3 + 1/x2, найти F(x)

(x3)′ = x4/4
(1/x2)′ = -1/x, =>
F(x) = x4/4 - 1/x + C

k - постоянная, то функция kF – первообразная для

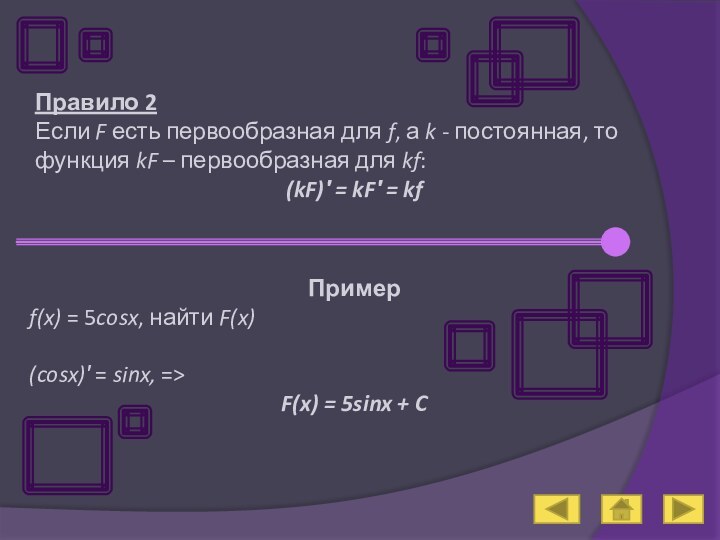
Пример
f(x) = 5cosx, найти F(x)

(cosx)′ = sinx, =>
F(x) = 5sinx + C