- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Методы решения уравнений
Содержание
- 2. Результат учения равенпроизведению способности на старательность.Если
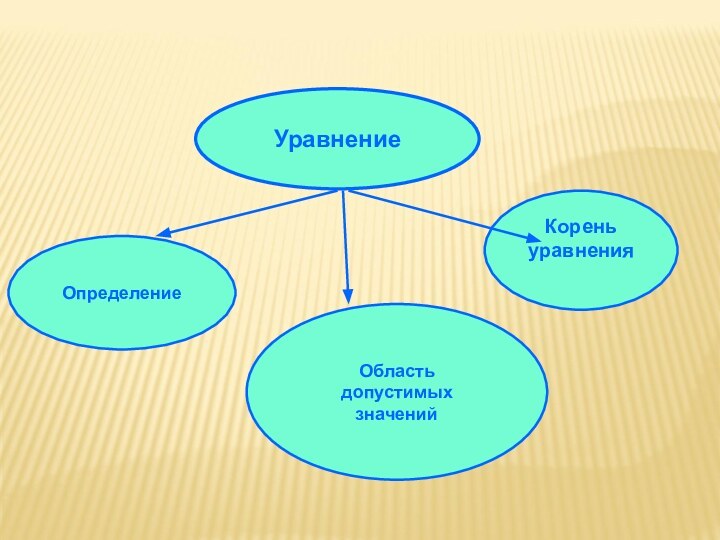
- 3. УравнениеОпределениеОбласть допустимых значенийКорень уравнения
- 4. Устно.Решить уравнение.
- 5. ОТВЕТЫ: 1) х=-2;2) решений нет;3) х=1;4) нет корней;
- 6. Найти область допустимых значений уравнений.
- 7. ОТВЕТЫ:-2≤Х ≤2;2) любое число;3) любое число, кроме ¾;4) х>5, кроме 6.
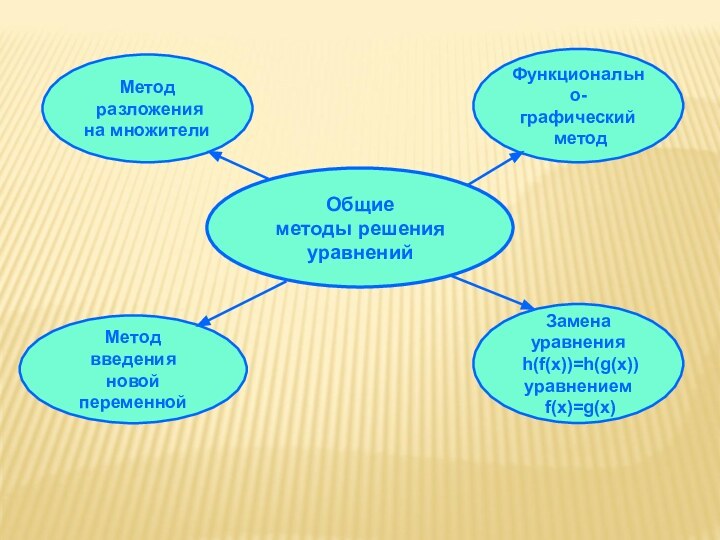
- 8. Общиеметоды решения уравненийМетод разложения на множителиМетодвведения новой переменнойЗамена уравнения h(f(х))=h(g(х))уравнением f(х)=g(х)Функционально-графический метод
- 10. ОТВЕТЫ:1) Замена уравнения h (f ( x
- 11. самостоятельная работа.
- 12. I уровень.Вариант №1.Решите уравнения.1.2.3.4.II уровень.
- 13. Ответы.I уровень.Вариант №1Вариант №2IIуровень.Вариант №1.Вариант №2.
- 14. Нестандартные уравнения. 1.022-10Решение. ОДЗ.ОДЗ этого уравнения
- 15. 2.log22(х3+х2+5)=0.Решение. Так как левая часть является суммой
- 16. Найдите целочисленный корень уравнения:10х-24-х2log2(7+6х-х2)- log2(х-2)=21.log12(6+5х-х2)Х2-9х+20=22.Ответ: 1) 5; 2) 3.
- 17. Скачать презентацию
- 18. Похожие презентации
Результат учения равенпроизведению способности на старательность.Если старательность равна нулю,то и все произведение равно нулю.А способности есть у каждого.















Слайд 2
Результат учения равен
произведению способности на старательность.
Если старательность
равна нулю,
у каждого.
Слайд 8
Общие
методы решения уравнений
Метод
разложения
на множители
Метод
введения
новой
переменной
Замена
уравнения
h(f(х))=h(g(х))
уравнением
f(х)=g(х)
Функционально-
графический
метод
Слайд 10
ОТВЕТЫ:
1) Замена уравнения h (f ( x ))
= h (g ( x ), уравнением f
(x) = g(x).2) Функционально-графический.
3) Замена уравнения h (f ( x )) = h (g ( x )), уравнением f (x) = g(x).
4) Замена уравнения h (f ( x )) = h (g ( x )), уравнением f (x) = g(x).
5) Перенести правый член уравнения в левую с противоположным знаком, преобразовать левую часть с помощью формул тригонометрии.
6) Метод разложения на множители.
7) Замена уравнения h (f ( x )) = h (g ( x )), уравнением f (x) = g(x).
8) Метод разложения на множители.
9) Метод введения новой переменной.
10) Метод введения новой переменной.
11) Функционально-графический.
12) Замена уравнения h (f ( x )) = h (g ( x ), уравнением f (x) = g(x).
Слайд 12
I уровень.
Вариант №1.
Решите уравнения.
1.
2.
3.
4.
II уровень.
II уровень.
Вариант №1. Вариант №2.
Решите уравнения. Решите уравнения.
1.
2.
3.
4.
I уровень.
Вариант №2.
Решите уравнения.
1.
2.
3.
4.
1.
2.
3.
4.
Слайд 14
Нестандартные уравнения.
1.
0
2
2
-1
0
Решение. ОДЗ.
ОДЗ этого уравнения состоит
из двух чисел х=2 и х=0.
Подставив данные значения в
исходное уравнение получим, х=2 корень данного уравнения.
Ответ: 2
Слайд 15
2.
log22(х3+х2+5)=0.
Решение.
Так как левая часть является суммой двух
неотрицательных слагаемых, то
х3+х2+5=1.
Решаем первое уравнение системы.
х2(х+2)-(х+2)=0,
(х+2)(х2-1)=0,
х1=-2; х2=-1; х3=1.
Подставляем найденные
значения во второеуравнение системы.
Если х=-2, то -8+2+5=1.
Если х=-1, то -1+1+5=1.
Если х=1, то 1+1+5=1.
Ответ: -2.





























